ÁNGULOS CUADRANTALES EJERCICIOS RESUELTOS PDF
RAZONES TRIGONOMÉTRICAS DE UN ÁNGULO CUADRANTAL
¿Qué es un ángulo cuadrantal?
Es un ángulo en posición normal que su lado final coincide o esta ubicado sobre un eje coordenado.
Su medida es siempre múltiplo de 90° y no pertenecen a ningún cuadrante.
medida de un ángulo cuadrantal =90°n ; n∈ℤ
¿Cuáles son los ángulos cuadrantales?
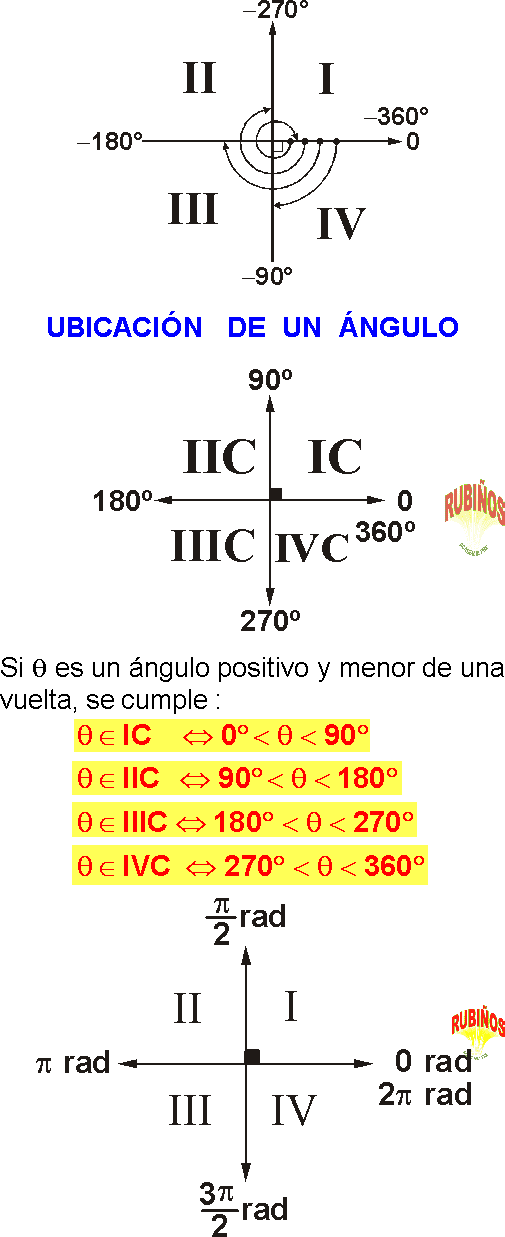
Los principales ángulos cuadrantes son: 0°, 90°, 180°, 270° y 360°, que por “comodidad gráfica” se escribirán en los extremos de los ejes.
APRENDIZAJES ESPERADOS
☛ Reconocer los ángulos cuadrantales.
☛ Determinar las razones trigonométricas de los ángulos cuadrantales.
☛ Calcular expresiones que contienen razones trigonométricas de ángulos cuadrantales.
Los ángulos cuadrantales son aquellos ángulos canónicos, cuyo lado final coincide con cualquiera de los semiejes cartesianos.
En consecuencia no pertenece a ningún cuadrante.
¿Cómo se sabe si un ángulo es cuadrantal ?
se hace lo siguiente:
El ángulo dado x se divide entre 90° o 𝛑/2 rad , dependiendo si x está en grados sexagesimales o en radianes. Si el resultado es un número entero, entonces, dicho ángulo x es cuadrantal.
Si θ es un ángulo positivo y mayor de una vuelta, se divide a entre 360° (2𝛑 rad) y se analiza el residuo.
RAZONES TRIGONOMÉTRICAS DE ÁNGULOS CUADRANTALES
Como ejemplo modelo vamos a calcular la R.T. de 90°, análogamente se va a calcular las otras R.T. de 0°; 180° ; 270° y 360°
El punto P(0;y) está sobre el lado terminal de 90°
Las razones trigonométricas de 0 y 360° son equivalentes por ser ángulos coterminales .
PRACTICA
EJERCICIO 1 :
Calcular: sen0°+ cos360°
Rpta. : "1"
EJERCICIO 2 :
Calcular:
sen𝛑+ sen𝛑/2 + sen3𝛑/2
Rpta. : "0"
EJERCICIO 3 :
Calcular:
sec0°+ csc𝛑/2+ cos𝛑/2
Rpta. : "1"
EJERCICIO 4 :
Calcular:
cos0°– 3sen𝛑+ 5tg0°
Rpta. : "1"
EJERCICIO 5 :
Determinar:
12tg0°+ 20232024cos90°
Rpta. : "0"
EJERCICIO 6 :
Calcular: tg0°+ ctg270°
EJERCICIO 7 :
Determinar:
(cos0°)152 + (csc90°)151
EJERCICIO 8 :
Calcular:
4 sec0°+ 2csc270°+ tg0°
EJERCICIO 9 :
Calcular:
10cos0°+ sec180°
EJERCICIO 10 :
Calcular:
sen90°.sec0° sec180 +csc90°