RELACIONES MÉTRICAS EN TRIÁNGULOS OBLICUÁNGULOS EJERCICIOS RESUELTOS PDF
APRENDIZAJES ESPERADOS
• Conocer las expresiones matemáticas para calcular las longitudes de las líneas notables de un triángulo.
• Comprender la relación existente entre los lados y ángulos de un triángulo cualquiera.
• Aplicar dichas relaciones en problemas tipo examen de admisión.
TRIÁNGULOS OBLICUÁNGULOS
El triángulo se clasifica en dos grupos: los triángulos rectángulos y los oblicuángulos, estos últimos se clasifican en dos el acutángulo y el obtusángulo.
Veremos las RELACIONES MÉTRICAS entre los elementos asociados en esos tipos de triángulos.
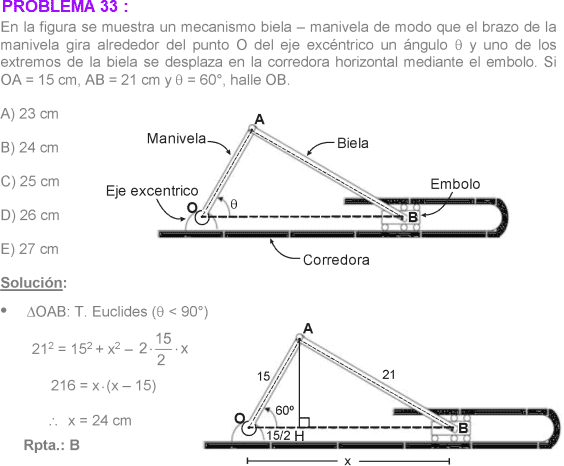
TEOREMA DE EUCLIDES :
I) TEOREMA DE EL CUADRADO DEL LADO OPUESTO A UN ÁNGULO AGUDO :
En todo triángulo oblicuángulo el cuadrado de la longitud del lado que se opone a un ángulo agudo es igual a la suma de los cuadrados de las longitudes de los otros dos lados menos el doble producto de la longitud de uno de estos lados por la longitud de la proyección del otro lado sobre el lado que se considera para el doble producto.
II) TEOREMA DEL CUADRADO DEL LADO OPUESTOS A UN ÁNGULO OBTUSO :
En todo triángulo oblicuángulo, el cuadrado de esa longitud del lado opuesto al ángulo obtuso, es igual a la suma de los cuadrados de las longitudes de los otros dos lados más el doble producto de la longitud de uno de estos lados por la proyección del otro lado sobre él.
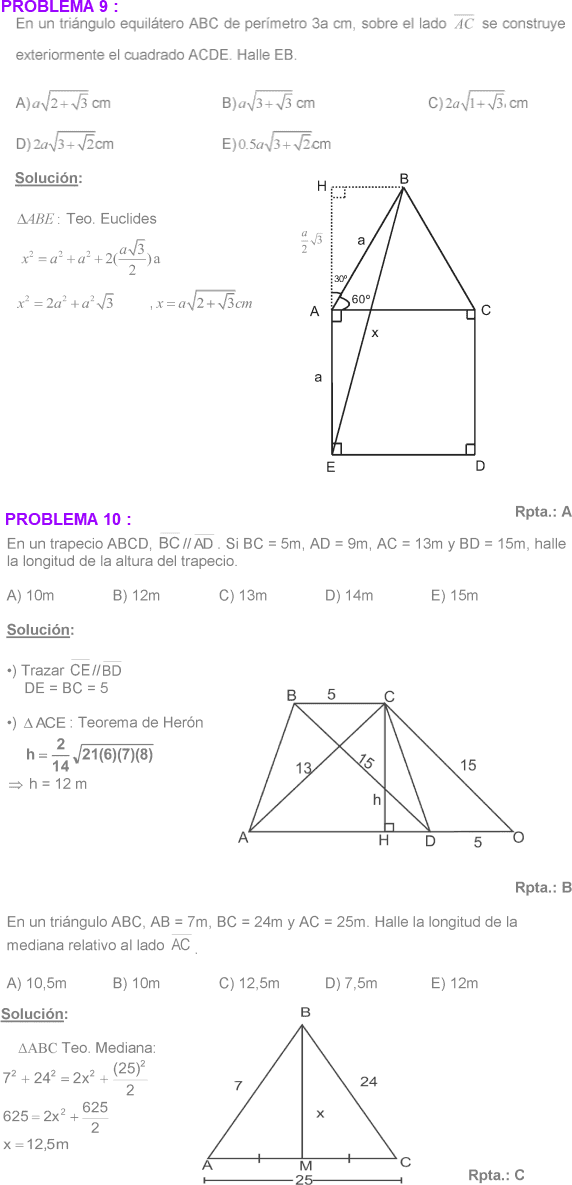
FÓRMULA DE HERÓN :
Nos sirve para determinar la longitud de la altura de un triángulo en función del semiperímetro y las longitudes de los lados del triángulo.
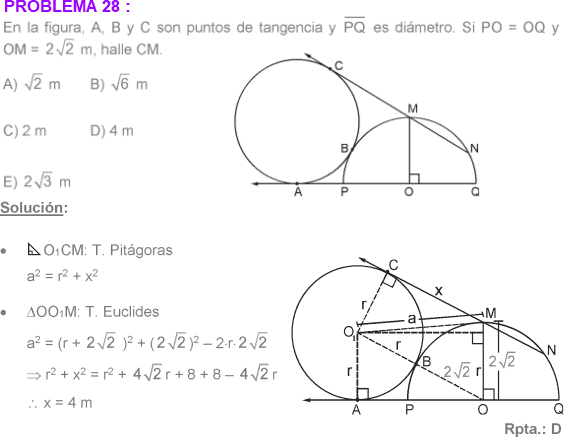
TEOREMA DE STEWARD:
Al trazar una ceviana cualquiera, su longitud se puede calcular en función de las longitudes de los segmentos que determina dicha ceviana y los lados del triángulo.
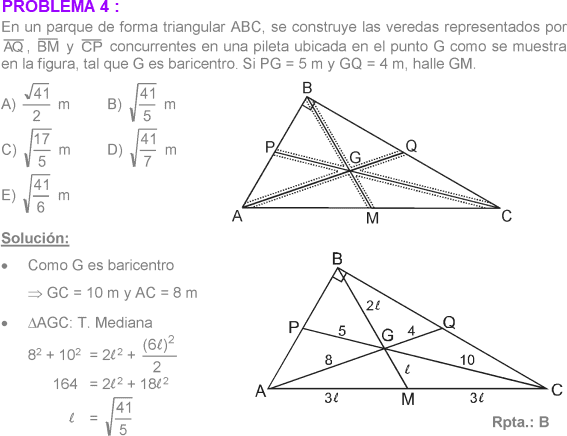
TEOREMA DE LA MEDIANA :
En todo triángulo se cumple que: dos veces el cuadrado de la longitud de la mediana relativa a un lado es igual a la suma de los cuadrados de las longitudes de los otros 2 lados, menos la mitad del cuadrado de la longitud del lado relativo a la mediana.
TEOREMA DE EULER :
En todo cuadrilátero; la suma de los cuadrados de los lados es igual a cuatro veces el cuadrado de la longitud del segmento que une los puntos medios de sus diagonales, más la suma de los cuadrados de dichas diagonales.
PRACTICA
PREGUNTA 1 :
Calcular el lado de un rombo sabiendo que el punto medio de un lado dista de los extremos del lado opuesto : 9 cm y 13 cm.
A) 8cm
B) 10
C) 9
D) 4
E) 2
Rpta. : "B"
PREGUNTA 2 :
En un triángulo ABC. Hallar la longitud de la mediana relativa al mayor lado, AB=4; BC=6 y AC=8.
A) √11
B) √10
C) √19
D) √14
E) √13
Rpta. : "B"
PREGUNTA 3 :
Calcular la longitud del segmento que une los puntos medios de las bases de un trapecio ; sabiendo que los lados laterales miden 5 y 7; y las bases se diferencian en 6 .
A) 2√7
B) 3√5
C) √7
D) √14
E) √13
Rpta. : "A"
PREGUNTA 4 :
Calcular el lado de un triángulo, sabiendo que la suma de los cuadrados de los otros 2 lados , es igual a 125 cm², y que las medianas relativas a estos 2 lados son perpendiculares.
A) 3 cm
B) 4
C) 5
D) 6
E) 2
Rpta. : "C"
PREGUNTA 5 :
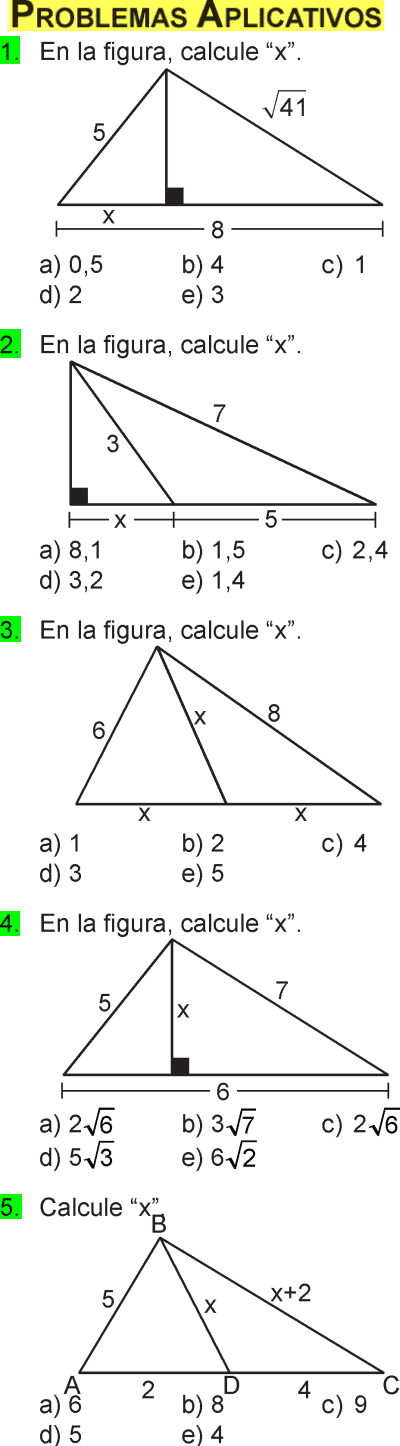
Los lados de un triángulo miden 5; √41 y 8. Calcular la medida de la menor altura.
A) 5
B) 4
C) 3
D)12
E) 1
Rpta. : "B"
PREGUNTA 6 :
En un triángulo, la suma de los cuadrados de los lados es 28. Hallar la suma de los cuadrados de las medianas del triángulo.
A) 20
B) 21
C) 19
D) 18
E) 17
Rpta. : "B"
PREGUNTA 7 :
Se tiene un trapecio ABCD; BC // AD; AB= √42; BC= 4; CD= 5 y AD= 10. Calcule la longitud del segmento que tiene por extremos los puntos medios de las bases de dicho trapecio.
A) 7√37/5
B) 5√3/3
C) 7√2/2
D) √7
E) 5
Rpta. : "B"
PREGUNTA 8 :
El cuadrilátero PQRS está inscrito en una circunferencia, siendo el lado PS su diámetro. Sea T el punto de intersección de las prolongaciones de los lados PQ y RS. Si PQ=7 u, RS=4 u y TR=6 u, entonces el valor de QR es
A) √37
B) √31
C) √41
D) √19
E) √23
Rpta. : "B"
PREGUNTA 9 :
Se tienen tres circunferencias tangentes exteriores dos a dos, con centros A, B y C respectivamente, donde AB= 5, AC= 7 y BC= 8, M ∈ BC es punto común de tangencia entre dos circunferencias. Determine AM.
A) √16
B) √17
C) √18
D) √19
E) √20
Rpta. : "B"
PREGUNTA 1 :
► El arco de Apolonio en medio de la antigua calle columnada con el ninfeo, en Antalya, Turquía. Apolonio de Perga, conocido como el gran geómetra, a quien se le atribuye el famoso teorema de la mediana.
► Uno de los principales problemas que tenían los agrimensores Egipcios (tensadores de cuerdas) era calcular la altura de un triángulo. Herón de Alejandría, planteo una formula para su cálculo
► Matthew Stewart 1717- 1785, matemático Escoces, continuador de los trabajos de Euclides y Apolonio, gran amigo de Robert Simson, ampliando algunas de sus ideas sobre el cálculo de una ceviana en un triángulo, que hoy es conocido como el teorema de Stewart