RELACIÓN DE ÁREAS CUADRANGULARES PROBLEMAS RESUELTOS

APRENDIZAJES ESPERADOS 

• Conocer la razón de áreas en regiones cuadrangulares

• Aprender la relación de áreas en regiones trapeciales así como en regiones paralelográmicas

• Aplicar lo aprendido en la resolución de problemas

PREGUNTA 1 : 

El área de una región cuadrangular convexa es 64 cm². Calcule el área de la región triangular que resulta de unir los puntos medios de tres lados. 

A) 28 𝑐𝑚²

B) 20 𝑐𝑚²

C) 12 𝑐𝑚²

D) 16 𝑐𝑚²

Rpta. : "D"

PREGUNTA 2 : 

En un paralelogramo ABCD se trazan DM (M en AB) y AC que se intersecan en P. 

Si MB= 2(AM), calcule la razón de áreas de las regiones APM y ABCD. 

A) 1/18 

B) 1/4

C) 1/8

D) 1/24

Rpta. : "D"

PREGUNTA 3 :

En la figura, AB // CD y AD // BC, las áreas de las regiones triangulares BTF y ATD son 16 cm² y 25 cm² respectivamente. Halle el área de la región ABCD

A) 89 cm² 

B) 88 cm² 

C) 85 cm² 

D) 80 cm² 

E) 90 cm² 

RESOLUCIÓN :

Rpta. : "E"

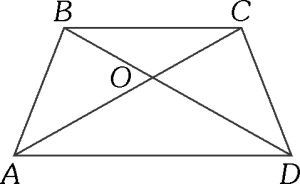
PREGUNTA 4 :   

En la figura adjunta, ABCD es un trapecio, donde las diagonales determinan los triángulos AOD y BOC de áreas 25 m² y 16 m², respectivamente. Calcular el área del trapecio.

A) 66 m² 

B) 70 m² 

C) 81 m²

D) 91 m²

E) 101 m² 

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 5 : 

Es un cuadrilátero ABC, el punto P divide al segmento AC en la razón 1/3 sobre 3 donde AP<PC. Si las áreas de las regiones triangulares ABD y BDC se miden 70 m² y 30 m², respectivamente, entonces el área de la región triangular PBD en m² es 

A) 45 

B) 44 

C) 42 

D) 40 

E) 39 

RESOLUCIÓN :

Rpta. : "A"

► Las regiones cuadrangulares son muy aprovechadas en el arte, así como en la textilería e infraestructuras. 

► En los planos de instalaciones se aprecia el aprovechamiento del espacio con las regiones cuadrangulares. 

► MUSCULO TRAPECIO 

El nombre se debe a la forma aplanada; en muchas ocasiones presentamos dolor en esa zona debido al estrés, una distensión muscular o una mala postura frente al ordenador.