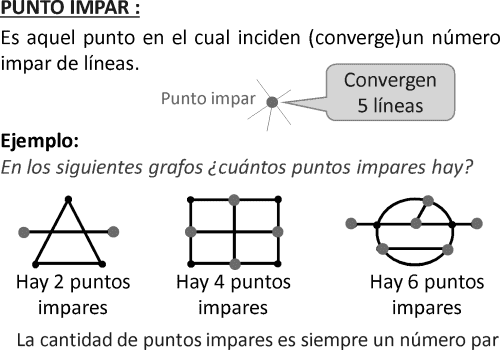
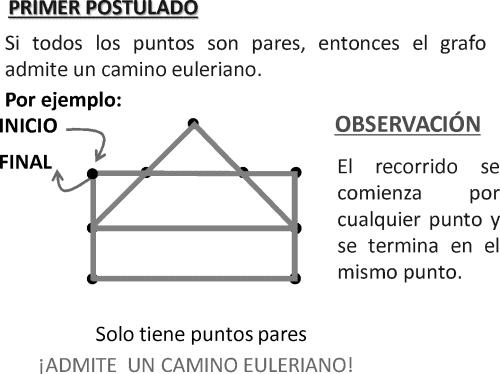
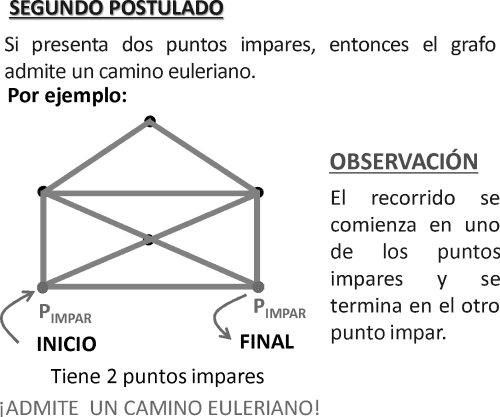
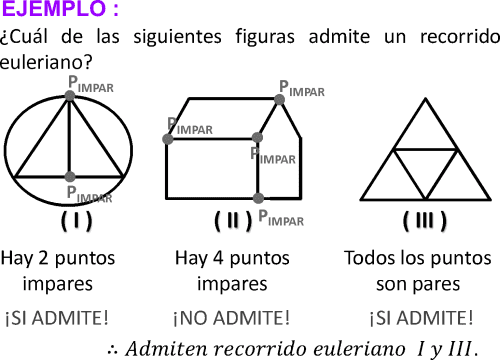
RECORRIDOS MÍNIMOS EULERIANOS EJERCICIOS RESUELTOS PDF HABILIDAD LÓGICO MATEMÁTICA
El objetivo de estudio será utilizar los diversos criterios prácticos para determinar el recorrido mínimo.
CÁLCULO DE RECORRIDOS MÍNIMOS
Cuando una figura tiene más de dos puntos impares, para recorrer por todas sus aristas de un trazo continuo se tendrá que repetir líneas.
Las líneas repetidas cumplen las siguientes condiciones condiciones:
• Van de un punto impar a otro punto impar.
• Son de longitud mínima.
• No son consecutivas (no parten de un vértice común).
► Cuando se repite una línea que une puntos impares se convierten dichos puntos impares en puntos pares.
► La longitud del recorrido mínimo queda determinado por la siguiente relación:
Longitud del recorrido mínimo = Longitud de las línea de la figura +Mínima longitud de las líneas repetidas
PROBLEMAS RESUELTOS
PREGUNTA 1:
La figura mostrada está formada por segmentos verticales y horizontales, las longitudes están dadas en centímetros. ¿Cuál será la menor longitud recorrida al dibujar la figura completa sin levantar la punta del lápiz del papel comenzando y terminando en el punto A?
A) 70 cm
B) 72 cm
C) 86 cm
D) 80 cm
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 2:
En la figura se muestra una estructura rectangular hecha de alambre. Si una hormiga se encuentra en el punto M, ¿ cuál es la mínima longitud que debe de recorrer la hormiga, para pasar por todo el alambrado y terminar finalmente en el punto N? (Longitudes en centímetros)
A) 83 cm
B) 84 cm
C) 85 cm
D) 86 cm
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 3 :
La figura está formada por rectángulos. ¿Cuál es la menor longitud, en centímetros, que debe de recorrer la punta de un lápiz, sin separarse del papel, para dibujar dicha figura, si se debe de comenzar desde el punto M?
A) 48
B) 46
C) 59
D) 49
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 4 :
Un pequeño robot es programado para recorrer todos los segmentos de una estructura, la cual está representada en la figura adjunta, en una escala de 1 a 20. Es decir, un 1 cm en la figura equivale de 20 cm de longitud real. Además, en la estructura, las líneas horizontales son paralelas al igual que las líneas verticales. ¿Cuál es la menor longitud que puede tener este recorrido? Dé como respuesta la longitud real.
A) 90 m
B) 17,40 m
C) 16 m
D) 18 m
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 5 :
La figura está formada por 10 cuadrados congruentes, cuyos lados miden 2 cm. ¿Cuál es la mínima longitud que debe recorrer la punta de un lápiz, para dibujar la figura de un solo trazo continuo, si se inicia en el punto M y se termina en el punto N?
A) 84 cm
B) 82 cm
C) 80 cm
D) 78 cm
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 6 :
Lenin le propone a Amy , darle de propina en soles el equivalente a la menor longitud que debe recorrer la punta de un lápiz, sin sepáralo del papel. Ella debe dibujar la figura mostrada, empezando en el punto “A” y terminando en el punto “B”, además se sabe que todos los cuadraditos tienen 2 cm de lado, ¿cuánto recibirá de propina Amy si cumple su objetivo?
A) S/ 100
B) S/ 86
C) S/ 106
D) S/ 120
RESOLUCIÓN :
Tramos horizontales: 4(4) + 3(2) = 22
Tramos verticales: 3(5) + 2(3) = 21
Tramos repetidos: 10
Total de tramos: 53×2 cm = 106 cm lo que equivale a S/. 106
Rpta. : "C"
PREGUNTA 7 :
En la figura se muestra una estructura de alambre conformada por un paralelepípedo y la mitad de un paralelepípedo. Si una hormiga se encuentra en el punto M, ¿cuál es la mínima longitud que debe de recorrer, para pasar por todo el alambrado y terminar en el único vértice par?
A) 88 cm
B) 98 cm
C) 98 cm
D) 92 cm
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 8 :
En la siguiente figura, se muestra 2 rectángulos idénticos, donde dos de sus lados se intersecan perpendicularmente en su punto medio. ¿Cuál es la mínima longitud que debe recorrer la punta de un lápiz, sin despegarse del papel, si se desea iniciar en el punto M y terminar en el punto N?
A) 87 cm
B) 75 cm
C) 80 cm
D) 83 cm
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 9 :
La figura mostrada esta formada por 15 cuadraditos congruentes cuyos lados miden 3 cm. Halle la longitud mínima que debe recorrer la punta de un lápiz sin separarla del papel para dibujar la figura.
A) 150 cm
B) 156 cm
C) 138 cm
D) 153 cm
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 10 :
La figura está formada por 5 hexágonos regulares congruentes de 4 cm de lado. ¿Cuál es la mínima longitud que debe de recorrer la punta de un lápiz para dibujar la figura de un solo trazo continuo, si debe de comenzar y terminar en el punto A?
A) 108 cm
B) 72 cm
C) 112 cm
D) 120 cm
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 11 :
La figura, representa una malla de forma rectangular, formada por doce rectángulos congruentes cuyos lados miden a centímetros y b centímetros. Sí a<b, 3a + 4b = 32 y a, b son números enteros, ¿ cuántos centímetros como mínimo, recorrerá la punta de un lápiz para dibujar la figura sin levantar el lápiz del papel?
A) 158 cm
B) 160 cm
C) 156 cm
D) 162 cm
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 12 :
Un camión recolector de basura debe recorrer las calles de una localidad, las cuales están representadas por todos los segmentos de la figura adjunta, en una escala de 1 a 20 000; es decir, 1 cm en la figura equivale a 20 000 cm de longitud real. Además, en la figura, las líneas horizontales son paralelas al igual que las líneas verticales. ¿Cuál es la menor longitud que puede tener este recorrido? Dé como respuesta la longitud real.
A) 29,6 km
B) 26,4 km
C) 30,4 km
D) 32 km
RESOLUCIÓN :
Rpta. : "A"





.png)
.png)
.png)
.png)
.png)
.png)

.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)


.png)
.png)



.png)

