TRIGONOMETRÍA EJERCICIOS RESUELTOS PDF
PREGUNTA 1 :
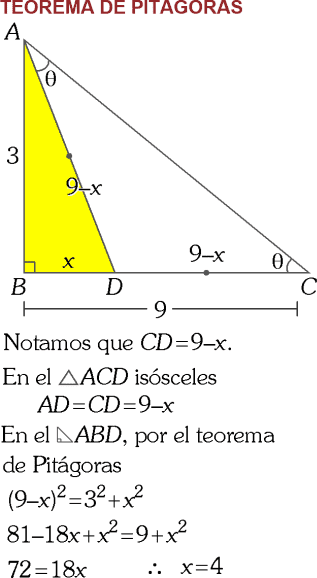
En la figura, determina el valor de x.
A) 2
B) 3
C) 8
D) 6
E) 4
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 2 :
En la figura determina el valor de b, si tanθ=20/21 y el perímetro es 492.
A) 134
B) 122
C) 129
D) 128
E) 126
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 3 :
En la figura, determina tanθ
A) 1/3
B) 1/8
C) 2/5
D) 1/4
E) 1/9
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 4 :
Desde un punto en la tierra ubicado a una distancia d de la base de un árbol, se observa la parte más alta con un ángulo de elevación β. El árbol es cortado a una altura h de su base, y al caer su punta forma con el suelo en ángulo θ.
Determina h/d
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 5 :
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 6 :
Si :
Determina el valor de E=49senθcosθ
A) √48
B) √49
C) √49/2
D) √44
E) √41
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 7 :
Si sen x + 2sen²x = 2, determine el valor de
A) 3
B) 2
C) 1
D) 4
E) 0
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 8 :
En la figura, ABCD es un rectángulo. Si AE=EB, AD=50, y
A) 150
B) 140
C) 200
D) 240
E) 180
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 9 :
La ecuación cos2t = cost describe el desplazamiento de un insecto, donde t denota el tiempo en segundos. ¿Cuál es el menor valor de t que satisface la ecuación?
A) 2𝛑/5
B) 4𝛑/3
C) 2𝛑/3
D) 2𝛑
E) 4𝛑
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 10 :
Calcule el valor de la expresión:
A) 28
B) 24
C) 26
D) 32
E) 30
RESOLUCIÓN :
Rpta. : "A"
EJERCICIOS DE ÁNGULOS VERTICALES CON RESPUESTAS
PREGUNTA 1 :
Una escalera de 6m de longitud es apoyada sobre una pared, formando con éste un ángulo de 30°, calcula la distancia entre los pies de la escalera y la pared.
a) 6
b) 4
c) 3
d) 8
e) 5
Rpta. : "C"
PREGUNTA 2 :
Un observador se encuentra a 24m de la base de un poste de 7m de altura. ¿Cuál es el ángulo de elevación respectivo?
a) 16°
b) 12°
c) 14°
d) 22°
e) 30°
Rpta. : "A"
PREGUNTA 3 :
La parte superior de un edificio de 48m de altura es observada bajo un ángulo de elevación de 53°. ¿Cuál es la distancia entre el observador y el pie del edificio?
a) 36 m
b) 32 m
c) 24 m
d) 38 m
e) 30 m
Rpta. : "A"
PREGUNTA 4 :
Desde lo alto de un edificio de 100m de altura se observa un auto estacionado bajo un ángulo de depresión de 60°. Calcula la distancia desde el auto hasta el pie del edificio en el punto que está bajo el observador.
a) 3√3/100
b) √3/3
c) 3√3
d) 5√3/100
e) √3
Rpta. : "A"
PREGUNTA 5 :
A 20 m del pie de un poste la elevación angular para lo alto del mismo es de 37°. ¿Cuál es la altura del poste?
a) 12 m
b) 10 m
c) 15 m
d) 14 m
e) 20 m
Rpta. : "C"
PREGUNTA 6 :
Desde la parte superior de un morro de 77m de altura se observa un objeto que está ubicado a 264m del pie del morro. ¿Cuál es el ángulo de depresión?
a) 14°
b) 16°
c) 12°
d) 10°
e) 15°
Rpta. : "B"
PREGUNTA 7 :
A 20 m de una torre se observa su parte más alta con un ángulo de elevación “θ” y si nos alejamos 10m el ángulo de elevación es el complemento de “θ”. Calcula Tgθ.
a) √(3/2)
b) √3
c) 2√3
d) √3/5
e) √2
Rpta. : "B"
PREGUNTA 8 :
Desde un punto A situado a 30m del pie de un edificio, se observa su parte superior con un ángulo de elevación de 30°. Calcula la distancia del punto A hacia la parte superior.
a) √3
b) 20√3
c) √3/2
d) 2√3
e) √5
Rpta. : "B"
PREGUNTA 9 :
Desde un punto en el suelo se observa la parte más alta de una torre con un ángulo de elevación de 60°. Si se retrocede 40m y se vuelve a observar la parte más alta, el ángulo de elevación es de 30°. Halla la altura de la torre.
a) 3√3
b) 10√3
c) 20√3
d) 3
e) √5
Rpta. : "C"
PREGUNTA 10 :
Desde un punto en el suelo se ubica la parte superior de un ángulo con una elevación angular de 37°. Nos acercamos 5m y la nueva elevación angular es de 45°. Halla la altura del árbol.
a) 12°
b) 14°
c) 15°
d) 10°
e) 8°
Rpta. : "C"
EJERCICIOS DE ÁNGULOS HORIZONTALES CON RESPUESTAS
PREGUNTA 1 :
Dos personas ubicadas al sur y este de un poste; divisan su parte más alta con ángulos de elevación de 30° y 45° respectivamente. Si la distancia entre las personas es de 20m. ¿Cuál es la altura del poste?
a) 20m
b) 5m
c) 15m
d) 10m
e) 10√2m
Rpta. : "D"
PREGUNTA 2 :
Una persona sale de su casa y hace el siguiente recorrido 37m hacia el norte, 40m al este, luego 108m al sur; para finalmente caminar con dirección NO 80√2m. ¿A qué distancia de su casa se halla?
a) 38m
b) 39m
c) 40m
d) 41m
e) 51m
Rpta. : "D"
PREGUNTA 3 :
Amy está ubicada en el centro de una pista circular; y camina al N40°E hasta ubicarse en la pista; de donde divisa la parte más nórdica de la pista al NαO. ¿Cuánto vale “α”?
a) 10°
b) 20°
c) 80°
d) 70°
e) 40°
Rpta. : "D"
PREGUNTA 4 :
Desde un punto “A” situado al sur de una torre BT se observa que el ángulo de elevación a la parte superior de la torre es de 45o y se camina 100√2mts en dirección Este hasta el punto C, el ángulo de elevación mide ahora 30o. Calcula la altura de la torre.
a) 50√2 m
b) 100 m
c) √2 m
d) 100√2 m
e) 200√2 m
Rpta. : "A"
PREGUNTA 5 :
Desde el centro de una circunferencia un móvil se desplaza en la dirección Eθ°N, hasta encontrar a la circunferencia. ¿Cuál debe ser el valor para que desde un punto se observe la parte más nórdica de la circunferencia en la dirección N60°θ .
a) 15°
b) 30°
c) 60°
d) 45°
e) 37°
Rpta. : "B"
PREGUNTA 6 :
Un móvil se desplaza 40√2m al NO; y luego 60m al este, de donde observa su punto de partida en la dirección OαS. Calcula “tanα”.
a) 1
b) 2
c) 3
d) 4
e) 6
Rpta. : "B"
PREGUNTA 7 :
Desde un punto “P” parten 2 autos hacia el Norte y el Este, a la misma velocidad. Luego de un cierto tiempo, parte del mismo punto otro auto en la dirección N37°E hasta ubicarse sobre la línea que une a los otros 2 autos. Si la distancia que separa a los dos primeros autos es de 21√2km. ¿Cuánto recorrió el tercer auto?
a) 5
b) 10
c) 15
d) 20
e) 25
Rpta. : "C"
PREGUNTA 8 :
Un faro tiene 31 m de altura, desde su parte más alta se observan dos barcos con ángulos de depresión de 30° y 45° respectivamente, uno al sur y el otro al este. Determina la distancia entre los barcos.
a) 50 m
b) 60 m
c) 62 m
d) 31 m
e) 40 m
Rpta. : "C"
PREGUNTA 9 :
La distancia entre 2 barcos “A” y “B” es de 12km y la recta que las une está en el rumbo E15°N de A. A medianoche una embarcación que navega hacia el S15°E con la velocidad uniforme de 10√3km/h está al NE de “A” y al “NO” de “B”. Halla el tiempo que emplea la embarcación en navegar la recta que une los barcos a partir de su posición en medianoche.
a) 10 min
b) 18 min
c) 20 min
d) 1 hora
e) 2 horas
Rpta. : "B"