SIMETRÍA Y REFLEXIONES EJERCICIOS RESUELTOS PDF HABILIDAD LÓGICA MATEMATICA

La simetría y la reflexión las podemos encontrar en elementos muy simples como el reflejo de un paisaje en un lago o una persona mirándose al espejo; pero también de formas más complejas, como elaborar una imagen con la ayuda de la computadora. 

EJE DE SIMETRÍA

Es una línea de referencia imaginaria que se usa para dividir una forma cualquiera en dos partes, en donde los puntos opuestos de estas son equidistantes entre sí, es decir, quedan simétricos. 

SIMETRÍA O REFLEXIÓN 

Se puede considerar una simetría como aquella transformación que aplicada a un punto, lo mueve 180° con respecto a un elemento de simetría, que puede ser una recta o un punto.

SIMETRÍA AXIAL 

Se da cuando los puntos de una figura coinciden con los puntos de otra tomando como referencia una línea que se llama eje de simetría. 

SIMETRÍA CENTRAL 

Es el reflejo de una imagen tomando como referencia un solo punto llamado punto de simetría. 

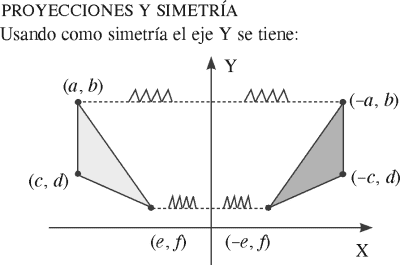
SIMETRÍAS CON RESPECTO A LOS EJES Y AL CENTRO 

PREGUNTA 1 :

La cuadricula, con algunos números y letras, que se muestra se va a doblar simétricamente por la línea más gruesa. ¿Cuál de las letras no va a coincidir con algún número de los mostrados en una misma casilla? 

A) E 

B) G 

C) A 

D) B 

RESOLUCIÓN :

En la figura se observa la letra que no coincide 

Rpta. : "A"

PREGUNTA 2 : 

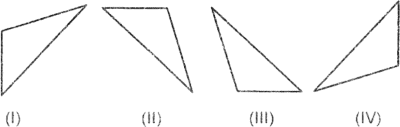
José ha dibujado dos rectas perpendiculares y un triángulo, como muestra la figura.

Luego de reflejar el triangulo de la figura usando como eje de simetria el eje Y, la figura que resulta es 

A) III     

B) IV     

C) II     

D) I 

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 3 :

La figura, en la que está un rectángulo dividido en cuatro zonas, se realiza dos simetrías, primero con respecto al eje Y, luego con respecto al punto A, en ese orden. 

¿Qué figura se obtiene al final? 

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 4 :

Taty pone frente a un espejo, que está en la pared de su cuarto, en esa posición, el sello que se muestra, ¿ qué reflejo de la figura que tiene el sello le muestra el espejo a Taty ? 

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 5 : 

RESOLUCIÓN :

• Reflejar con respecto al eje X y luego con respecto al eje Y, equivale a un reflejo con respecto al origen de coordenadas. 

• Reflejar con respecto al origen de coordenadas hace que la figura gire 180°.

Rpta. : "D"

PREGUNTA 6 : 

Un arquitecto está diseñando el plano de un parque que tiene la forma de un paralelogramo, el cual está representado en la figura adjunta. El arquitecto decide cambiar la posición del parque, para lo cual realiza dos reflexiones. La primera y la segunda reflexión del paralelogramo se realizan tomando como eje de simetría el eje X y el eje Y, respectivamente. Halle las abscisas de los vértices de la figura que se obtiene luego de realizar ambas reflexiones. Dé como respuesta la suma de estas. 

A) – 4     

B) – 8     

C) – 6     

D) – 10 

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 7 :

El número trece se refleja como muestra la figura de la izquierda. Si ocurre lo mismo en la figura de la derecha, ¿qué figura se obtiene donde aparece el signo de interrogación? 

RESOLUCIÓN :

Siguiendo la regla que se muestra con el número 13 vemos el siguiente resultado: 

Rpta. : "A"

PREGUNTA 8 :

El número cuatro está frente a dos espejos y se refleja como muestra la figura. Si ocurre lo mismo con el número diecisiete, ¿cuál figura se obtiene donde aparece el signo de interrogación? 

RESOLUCIÓN :

Siguiendo los reflejos tenemos que 

Rpta. : "A"

PREGUNTA 9 :

De la figura, encuentre los vértices del triángulo A’B’C’ como reflejo de la imagen del triángulo ABC con respecto a la recta y = –2. Dé como respuesta la suma de las coordenadas de los puntos A y C’. 

A) 12 

B) 13 

C) 14 

D) 15 

RESOLUCIÓN :

A(6,4) 

B’(3,–4); A’(6,–8);C’(9,–6) 

6 + 4 + 9 – 6 = 13 

Rpta. : "B"

PREGUNTA 10 :

Edu ha dibujado en una hoja dos rectas perpendiculares y un triángulo como se muestra en la figura. Dichas rectas se usan como un sistema de coordenadas y el origen de coordenadas como un punto de simetría para construir un nuevo triángulo. Calcule la suma de los números que representan a las coordenadas de los vértices del nuevo triángulo. 

A) 2 

B) 4 

C) –3 

D) –4 

RESOLUCIÓN :

► Coordenadas: (–4,5) ; (–4,0) ; (–1,2) Simetría con respecto a origen de coordenadas: (0,0) (4,–5) ; (4,0) ; (1,–2) 

► Suma de los números que conforman las coordenadas = 2 

Rpta. : "A"

PREGUNTA 11 :

De la figura, encuentre los vértices del triángulo A’B’C’ como reflejo de la imagen del triángulo ABC con respecto a la recta x = –3. De cómo respuesta la suma de las coordenadas de los puntos B’ y C’. 

A) –10 

B) –11 

C) –12 

D) –15 

RESOLUCIÓN :

De la figura: A´(–9,3); B´(–11,7) y C´(–14,3). 

Luego: –11 + 7 + –14 + 3 = –15 

Rpta. : "D"

PREGUNTA 12 :

Hemos colocado una ruleta hexagonal regular frente a un espejo que se encuentra pegado a la pared, como se muestra en la figura; de manera que la ruleta se refleje en el espejo. Si Carlitos gira la ruleta mostrada 600 en sentido horario, ¿cuál es la imagen de la ruleta, después de hacerla girar, que visualizara Carlitos en el espejo? 

RESOLUCIÓN :

En la figura se muestra el giro necesario y el reflejo 

Rpta. : "D"

PREGUNTA 13 : 

Un estudiante decide cambiar la posición del triángulo de la figura adjunta. Para ello, realiza dos reflexiones: primero, toma como eje de simetría Y y, luego, X. Tras estas dos reflexiones, halle las ordenadas de los vértices del triángulo y dé como respuesta el producto de estas.

A) – 18    

B) 9    

C) 18    

D) – 9 

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 14 :

Determine las coordenadas del punto simétrico de A = (–4;6) respecto del punto P = (–1;2) 

A) (–3;2) 

B) (2;–2) 

C) (3;–3) 

D) (0;–2) 

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 15 :

Considerando que el centro de un cuadrado de lado 2 unidades es el origen de coordenadas (0,0), halle la suma de las componentes de los vértices del cuadrado simétrico con respecto al punto (3,4). 

A) 55 

B) 56 

C) 57 

D) 54 

RESOLUCIÓN :

Sean los vértices del cuadrado original A (1;1) , B (1;–1) , C (–1;–1) y D (–1;1) y sus reflejos con respecto a (3;4) son A’; B’; C’ y D’ 

Considerando que el punto medio de A y A’ es (3;4) entonces tenemos A= (5; 7), de manera análoga para los otros vértices B’ (5; 9) , C’ ( 7; 9) , D’ ( 7; 7 )

Piden: 5+7+5+9+7+9+7+7=56 

Rpta. : "B"

PREGUNTA 16 :

Se tiene el dibujo de un plano ABCD como se muestra en el gráfico. Tomando primero a la recta Y=–2 como eje de simetría, y luego a la recta X=3, también como eje de simetría, ¿cuánto es la suma de las coordenadas de los vértices de la imagen que se obtiene en el último paso? 

A) –12 

B) –8 

C) –32 

D) –5 

RESOLUCIÓN :

Las coordenadas de los vértices son: 

A(2,3) 

B(3,7) 

C(8,7) 

D(7,3) 

Tomando al eje Y=-2 como eje de reflexión tenemos: 

A’(2,-7) 

B’(3,-11) 

C’(8,-11) 

D’(7,-7) 

Tomando al eje X=3 como eje de reflexión tenemos:

 A’’(4,–7) 

B’’(3,–11) 

C’’(-2,–11) 

D’’(-1,–7) 

Suma de coordenadas: 4 – 7+3-11 – 2 – 11 – 1 – 7=–32 

Rpta. : "C"

PREGUNTA 17 :

Elida tiene 50 fichas cuadradas congruentes y con 17 de ellas ha formado una figura como la que se representa en la figura. Sin mover las fichas ya colocadas, ¿cuántas de las fichas que le quedan, debe agregar como mínimo, de modo que la línea que se indica sea un eje de simetría de la figura resultante? 

A) 4 

B) 5 

C) 8 

D) 7 

RESOLUCIÓN :

En la figura se indican los cuadrados necesarios que se deben agregar para que la figura resultante sea simétrica respecto de la línea indicada. 

Rpta. : "A"

PREGUNTA 18 :

En el gráfico dado se tiene el sistema de coordenadas rectangulares, donde cada cuadradito representa una unidad, además se muestra un pentágono de vértices ABCDE. Primero reflejamos el pentágono ABCDE usando como eje de simetría el eje Y y se obtiene el pentágono de vértices A‘B‘C‘D‘E‘; por último reflejamos el pentágono A‘B‘C‘D‘E‘ usando como eje de simetría el eje X, obteniendo un pentágono de vértices A‘‘B‘‘C‘‘D‘‘E‘‘. Halle la suma de las coordenadas de los vértices A‘‘B‘‘C‘‘D‘‘E‘‘. 

A) –61 

B) 61 

C) 10 

D) –10 

RESOLUCIÓN :

Con respecto al eje Y (cambia de signo la abscisa) y después con respecto al X (cambia el signo de las ordenadas): 

A(3,8) → A‘(–3,8) → A‘‘(–3,–8) 

B(5,10) → B‘(–5,10) → B‘‘(–5,–10) 

C(7,8) → C‘(–7,8) → C‘‘(–7,–8) 

D(6,5) → D‘(–6,5) → D‘‘(–6,–5) 

E(4,5) → E‘(–4,5) → E‘‘(–4,–5). 

Suma de coordenadas: 

– 8 – 3 – 10 – 5 – 8 – 7 – 5 – 6 – 5 – 4 = – 61. 

Rpta. : "A"

PREGUNTA 19 :

Aby ha dibujado en una hoja cuadriculada dos rectas perpendiculares y un polígono como se muestra en la figura. Se construye una figura simétrica usando como punto de simetría el punto que se indica. Si la hoja la usa como un plano coordenado (en el cual cada cuadradito representa una unidad); y las rectas representan a los ejes coordenados, indique la suma de los números que forman las coordenadas de los vértices de la figura construida. 

A) 38 u 

B) 37 u 

C) 35 u 

D) 36 u 

RESOLUCIÓN :

► En la figura se indica el proceso respectivo. 

► La suma de los números de las coordenadas que se indican es: 52 – 16 = 36 

Rpta. : "D"

PREGUNTA 20 :

Se ubica en el plano cartesiano el segmento de extremos A (–5;–2) y B(–2;–6). Determine las coordenadas de los segmentos simétricos con respecto al eje Y, al eje X y al origen de coordenadas. Dé como respuesta la suma de las coordenadas de los extremos de los segmentos simétricos. 

A) 15 

B) –9

C) –3 

D) 0 

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 21 :

La figura, al polígono de 6 lados, con la cual se realiza dos simetrías. Primero con respecto al eje de simetría y luego con respeto al punto que se indica, en ese orden. Si consideramos la posición de la figura final respecto del punto A, ¿qué figura se obtiene? 

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 22 :

Amy ubica en un plano cartesiano el segmento de extremos M(2;6) y C(5;2) a dicho segmento lo refleja primero con respecto al eje X, para luego construir una figura simétrica respecto al punto (–1:0). Indique las coordenadas de los extremos del segmento construido en este último paso. 

A) (–1;2) y (–4;6) 

B) (–4;6) y (–7;2) 

C) (3;-3) y (5;2) 

D) (2;–2) y (4;3) 

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 23 :

El segmento AB, se debe reflejar respecto de la recta vertical L y luego, obtener su imagen simétrica, respecto del punto P. Calcule las coordenadas del punto medio, del segmento que se obtiene al final del proceso. 

A) (1,5; 3,5) 

B) (2,5; 4,5) 

C) (3,5; 4,5) 

D) (2,5; 3,5) 

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 24 :

Se ubica en el plano cartesiano el triángulo de vértices A (–7;–4) B (–6;3) C (–2;–1) y la recta x=–1 paralela al eje Y, a dicho triángulo se le aplica una simetría con respecto a la recta L. ¿Cuál es la suma de las coordenadas de los vértices del triángulo A´B´C´? 

A) 3 

B) 4 

C) 6 

D) 7 

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 25 :

Estela ha dibujado en una hoja cuadriculada dos rectas perpendiculares y la línea MC como se muestra en la figura. A la línea MC la refleja respecto del eje que se indica, y luego a partir de esta última figura construye una figura simétrica usando como punto de simetría el punto P (–6,0). Si la hoja la usa como un plano coordenado (donde cada cuadradito es una unidad) y las rectas representan a los ejes coordenados, indique la suma de los números que forman las coordenadas de los puntos M y C de la figura construida en el último paso. 

A) –15 u 

B) –11 u 

C) –24 u 

D) –23 u 

RESOLUCIÓN :

Los puntos serían (–4;–4), (–7;–8), la suma es –23. 

Rpta. : "D"

PREGUNTA 26 :

Felix ha dibujado en una hoja cuadriculada dos rectas perpendiculares y 4 vértices A, B, C y D de un cuadrado. Dichos vértices los refleja respecto del eje de simetría que se indica, obteniendo los puntos A′, B′, C′ y D′ respectivamente, en la figura solo se ve 3 de ellos. Si la hoja la usa como un plano coordenado (en el cual cada cuadradito representa una unidad); y las rectas representan a los ejes coordenados, indique la suma de los números que forman las coordenadas de los vértices A, B, C y D. 

A) 25 

B) 28 

C) 30 

D) 32 

E) 29 

RESOLUCIÓN :

1+8+5+6+3+2-1+4=28 

Rpta. : "B"

PREGUNTA 27 :

Juneth ha dibujado en una hoja cuadriculada dos rectas perpendiculares y un polígono como se muestra en la figura. Se construye una figura simétrica usando como punto de simetría el punto que se indica. Si la hoja la usa como un plano coordenado (en el cual cada cuadradito representa una unidad); y las rectas representan a los ejes coordenados, indique la suma de los números que forman las coordenadas de los vértices de la figura construida. 

A) 8 u 

B) 7 u 

C) 5 u 

D) 9 u 

E) 6 u 

RESOLUCIÓN :

► En la figura se indica el proceso respectivo. 

► La suma de los números de las coordenadas que se indican es: 32 – 23 = 9 

Rpta. : "D"

PREGUNTA 28 :

La figura, en la que esta una estrella de cuatro puntas, se realiza dos simetrías, primero con respecto al punto que se indica y luego a con respecto a la recta L, mostrada, en ese orden. ¿Qué figura se obtiene al final? 

RESOLUCIÓN : 

En la figura se indica el proceso de simetría y los respectivos resultados. 

Rpta. : "A"

PREGUNTA 29 :

Se ha dibujado en una hoja cuadriculada, dos rectas perpendiculares (ejes coordenados), el polígono A, B, C, D, E, F y la recta L // eje Y como se muestra en la figura. A este polígono, se le aplica una simetría respecto a la recta L. Si la hoja la usa como un plano coordenado, indique la suma de los números que forman las coordenadas de los vértices de la figura trasformada. 

A) –8 

B) –9 

C) –10 

D) –11 

RESOLUCIÓN :

En la figura se indica el proceso respectivo. 

A(–4, –4) → A’(0, –4) 

B(–6, –2) → B’(2, –2) 

C(–5,1) → C’(1,1) 

D(–3,3) → D’(–1,3) 

E(1,3) → E’(–5,3) 

F(3, –2) → F’(–7, –2) 

La suma de los números de las coordenadas que se indican es: 

(2+1+1+ 3+3) – (4+2+1+5+7+2) = –11 

Rpta. : "D"

PREGUNTA 30 :

De la figura, encuentre los vértices del triángulo A’B’C’ que es el triángulo simétrico del triángulo ABC con respecto a la recta x = –1. De cómo respuesta la suma de las coordenadas de los puntos B’ y C’. Si las coordenadas de los vértices son A(3,2), B(6,6) y C(9,4). 

A) –9 

B) –8 

C) –10 

D) –11

E) –7 

RESOLUCIÓN :

Se tiene: 

De la figura: A’(–5,2); B´(–8,6) y C´(–11,4). 

Luego: –8 + 6 + –11 + 4 = –9 

Rpta. : "A"

PREGUNTA 31 :

Eli ha dibujado en una hoja cuadriculada dos rectas perpendiculares y una bicicleta como se muestra en la figura. A la imagen de la bicicleta se la refleja respecto del eje que se indica, y luego a partir de esta última figura construye una figura simétrica usando como punto de simetría el punto que se indica. Si la hoja la usa como un plano coordenado (donde cada cuadradito es una unidad) y las rectas representan a los ejes coordenados, indique la suma de los números que forman las coordenadas del punto L de la figura construida en el último paso. 

A) –5 u 

B) –1 u 

C) –2 u 

D) 0 u 

E) 2 u 

RESOLUCIÓN :

El punto sería (–7; 7) la suma es 0. 

Rpta. : "D"

PREGUNTA 32 :

Se tiene el triángulo ABC de vértices A= (1; 2), B= (–1; 5) y C= (–3; –1). ¿Cuál es la suma de las abscisas de los vértices del triángulo reflejado del triángulo ABC con respecto a la recta L: x= 3? 

A) 17 

B) 19 

C) 20 

D) 21 

Rpta. : "D"

PREGUNTA 33 :

Del cuadrado ABCD se sabe que A= (1; 1), B= (1; –4) y C= (6; –4). A dicho cuadrado se le aplica una simetría central con respecto al origen de coordenadas. Halle la menor suma de coordenadas de uno de los vértices del cuadrado simétrico resultante. 

A) –2 

B) – 5 

C) –7 

D) –10 

Rpta. : "C"

PREGUNTA 34 :

En el plano cartesiano, se ubica el segmento de extremos A(–7; 2) y B(–1; 5). Determine las coordenadas de los segmentos simétricos con respecto al eje Y, al eje X y al origen de coordenadas. Dé como respuesta la suma de las coordenadas de los extremos de los segmentos simétricos. 

A) 3 

B) 1 

C) –1 

D) –2 

Rpta. : "B"

PREGUNTA 35 :

Edu ha dibujado en una hoja cuadriculada dos rectas perpendiculares y un triángulo, tal como se muestra en el gráfico. A la figura triangular la refleja respecto del eje que se indica, y luego construye una figura simétrica usando como punto de simetría el punto que se indica. Si usa la hoja como un plano coordenado y las rectas representan a los ejes coordenados, indique la suma de los números que forman las coordenadas de los vértices de la figura construida en el último paso. 

A) –10 

B) –11 

C) – 4 

D) – 9 

Rpta. : "B"

PREGUNTA 36 :

En el gráfico se muestra un sistema de coordenadas cartesianas, en el cual se tiene el cuadrilátero MNPQ. Los vértices M y P son simétricos con respecto al origen de coordenadas O, y los vértices N y Q son simétricos respecto al eje Y. Si M(–2; 6) y N(–7; 3), halle la suma de las coordenadas de P y Q. 

A) 5 

B) 0 

C) 8 

D) 6 

Rpta. : "D"