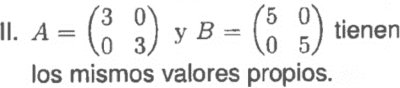UNI 2025-2 SEGUNDA PRUEBA RESUELTA RESPUESTAS INGRESO UNIVERSIDAD PDF MATEMÁTICA
PREGUNTA 1
Si el siguiente número
es capicúa, calcule la suma de las cifras de N.
A) 32
B) 33
C) 34
D) 35
E) 36
Resolución
Clave B
PREGUNTA 2
Halle el valor de A2+B2+C2
A) 21
B) 23
C) 25
D) 27
E) 36
Resolución
Clave C
PREGUNTA 3
La media aritmética de dos números naturales es 15 y su media geométrica es 12. Halle la diferencia de dichos números.
A) 12
B) 16
C) 18
D) 24
E) 30
Resolución
Clave C
PREGUNTA 4
Sean n y m dos números naturales tales que al dividir n entre m resulta un cuadrado perfecto, donde
y m es el menor número con esta propiedad.
Halle la suma de las cifras del número n+m.
A) 21
B) 22
C) 23
D) 24
E) 25
Resolución
Clave D
PREGUNTA 5
En un campeonato de fútbol participan 20 equipos que serán repartidos en dos ligas con igual número de equipos. Entonces la probabilidad que los dos equipos más poderosos estén en ligas diferentes es
A) 9/38 .
B) 11/38 .
C) 16/38 .
D) 20/38 .
E) 21/38 .
Resolución
Clave D
PREGUNTA 6
Se quiere fabricar una tolva para granos en forma de cono truncado y compuesto de 11 anillos metálicos como se muestra en la figura. Halle la longitud total del metal necesario para fabricar los anillos.
A) 228𝛑
B) 231𝛑
C) 234𝛑
D) 237𝛑
E) 240𝛑
Resolución
Clave B
PREGUNTA 7
En una matriz cuadrada A, se denomina valor propio de A, a los valores x, que resuelvan la ecuación siguiente:
|A−xI| = 0
donde I es la matriz identidad.
Dadas las siguientes proposiciones:
I. A y AT poseen los mismo valores propios.
III. Toda matriz simétrica, de términos reales no nulos de orden 2×2 posee dos valores propios reales y diferente.
Indique la alternativa correcta:
A) Solo I
B) Solo II
C) Solo III
D) I, II y III
E) I y III
Resolución
Clave E
PREGUNTA 8
Halle a+2b.
A) 32
B) 33
C) 34
D) 35
E) 36
Resolución
Clave C
PREGUNTA 9
El siguiente es el reporte de la productividad de dos tipos de calculadoras.
¿Cuántos de cada tipo se deben fabricar para obtener la mayor ganancia si se venden todas las calculadoras?
A) (4; 3)
B) (5; 3)
C) (3; 4)
D) (16; 3)
E) (8; 4)
Resolución
Clave C
PREGUNTA 10
Para un problema de programación lineal, indique la secuencia correcta después de determinar si la proposición es verdadera (V) o falsa (F):
I. La solución óptima se puede encontrar en un punto interior de la región factible.
II. Cuando la región factible es no acotada, la solución óptima siempre es no acotada.
III. El problema “mínz=cx” s.a Ax≤b tiene solución óptima x* y el problema “mínz=–cx” s.a Ax≥b tiene solución óptima –x*.
A) VFV
B) VFF
C) FFV
D) FVF
E) FFF
Resolución
Teorema fundamental de la programación lineal: Este teorema establece que si existe una solución óptima, dicha solución se encuentra en uno de los vértices de la región factible. Un vértice es un punto donde se interceptan varias restricciones, y no puede ser expresado como una combinación convexa de otros puntos factibles.
I. La solución óptima siempre se encontrará en la frontera de la región factible.
Clave E
PREGUNTA 11
La longitud de un arco de circunferencia es 10𝛑 m. Si la longitud del radio aumenta en 50% y la medida del ángulo central disminuye en 20%, calcule la longitud (en m) del nuevo arco.
A) 8𝛑
B) 10𝛑
C) 12𝛑
D) 13𝛑
E) 14𝛑
Resolución
Clave C
PREGUNTA 12
En la prolongación de CA de un triángulo acutángulo ABC se ubica el punto D, tal que AC=4(DA). DB=BC y m∢ACB=45°. Si BC=5√10. Calcule AB (en cm).
A) √170
B) √175
C) √180
D) √185
E) √190
Resolución
Clave A
PREGUNTA 13
En la figura mostrada O es centro del arco AC, B es el centro del arco MN cuyo radio mide r y Q es el centro de la circunferencia cuyo radio mide r1. Si T y P son puntos de tangencia, calcule r1/r
A) √3/3
B) √2/4
C) √2/2
D) √3/4
E) √2/3
Resolución
Clave B
PREGUNTA 14
En una superficie esférica de longitud de radio R, el área de una zona esférica cuya altura mide R/4 es equivalente al área de un huso esférico. Calcule la medida (en grados sexagesimales) del ángulo diedro correspondiente al huso esférico.
A) 15
B) 30
C) 45
D) 60
E) 75
Resolución
Clave C
PREGUNTA 15
Las caras de un triedro equilátero miden 45°. Determine la medida (en grados sexagesimales) de una de las caras del triedro polar, cuyo vértice está en el interior del triedro dado.
A) arc cos( √3 – √2)
B) arc cos(1 – √2)
C) arc cos(1 – √3)
D) arc cos( √2 – √3)
E) arc cos( √3 – 1)
Resolución
Clave B
PREGUNTA 16
En un triángulo ABC de lados BC=a, AC=b; donde 3a=5b. Calcule
A) 1
B) 2
C) 3
D) 4
E) 6
Resolución
Clave D
PREGUNTA 17
En la figura adjunta, ℓ y L son datos. Calcule tan2θ.
Resolución
Clave B
PREGUNTA 18
Resuelva la ecuación:
2cos2(x)+3sen(x)=0
e indique la suma de soluciones en [0; 2𝛑]
A) 𝛑/6
B) 5𝛑/6
C) 7𝛑/6
D) 11𝛑/6
E) 3𝛑
Resolución
Clave E
PREGUNTA 19
En la figura adjunta, calcule el valor del ángulo α.
A) –125°
B) –135°
C) –145°
D) –175°
E) –225°
Resolución
Clave E
PREGUNTA 20
Calcule el área aproximada (en cm2) de la región limitada por los lados de un triángulo que miden 2√2 cm, 3√6 cm, 5√3 cm.
A) 8,78
B) 9,87
C) 10,12
D) 10,55
E) 10,69
Resolución
Clave B
