GEOMETRIA EXAMEN BECA 18 PRONABEC ADMISIÓN UNIVERSIDAD PRUEBA ÚNICA NACIONAL RESUELTA PDF
PREGUNTA 1 :
Se tiene un paralelogramo ABCD, de modo que AB=12 y BC=5; se traza la bisectriz interior AE (E en DC). Si el área de la región paralelográmica es 48u2, calcula el área de la región AECB.
A) 44 u2
B) 28 u2
C) 36 u2
D) 38 u2
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 2 :
Se tiene un triángulo equilátero ABC de lado 12, MN//AC . Si AM=10.
Calcula el área de la región del triángulo ABN.
A) 3√3
B) 6√3
C) 4√3
D) 5√3
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 3 :
En un cuadrado ABCD, si la intersección entre AC y BM es N; AM=MD y la distancia de N a AM es 20 u.
Calcula el área de la región cuadrada ABCD.
A) 1800 m2
B) 3600 m2
C) 4800 m2
D) 2700 m2
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 4 :
Se tiene un sector circular cuyo ángulo central es 2𝛑/5 rad . Calcula la relación de áreas de dicho sector y el círculo al cual pertenece.
A) 2/5
B) 1/4
C) 1/6
D) 1/5
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 5 :
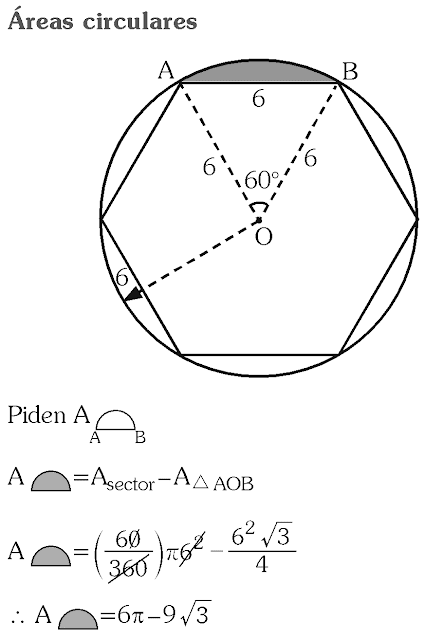
En un hexágono regular inscrito en una circunferencia de radio 6 u, calcula el área de uno de los segmentos circulares determinados por un lado del hexágono regular y la circunferencia.
A) 7π – 6√3
B) 6π – 9√3
C) 8π – 9√3
D) 9π – 6√3
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 6 :
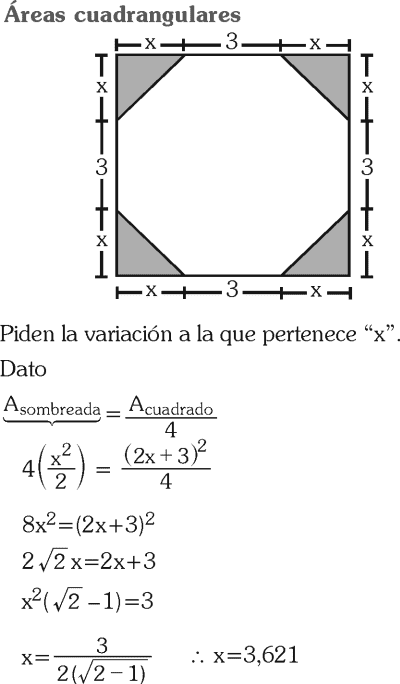
En el gráfico, la suma de las áreas de las regiones sombreadas isósceles es igual a la cuarta parte del área de la región cuadrada ABCD; encuentra a qué intervalo pertenece “x”.
A) 0,5 < x < 1
B) 1 < x < 2,5
C) 2,5 < x < 3,1
D) 3,1 < x < 4
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 7 :
En la pirámide P–ABC, de altura PA , M es punto medio de PC y AM=BC. Si m∠ABC=90°, calcula el orden de las medidas de los ángulos CPB , PCB y PBC.
A) 45°, 45°, 90°
B) 30°, 75°, 75°
C) 30°, 60°, 90°
D) 60°, 60°, 60°
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 8 :
En una semicircunferencia de diámetro AB=12 cm se inscribe el triángulo ACB, por el centro de la semicircunferencia se traza una paralela de AC interceptando a BC en Q y en P a la tangente trazada a la circunferencia en B. Si BC=8, calcula PB.
A) 2√2
B) 3√2
C) 5√2
D) 10
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 9 :
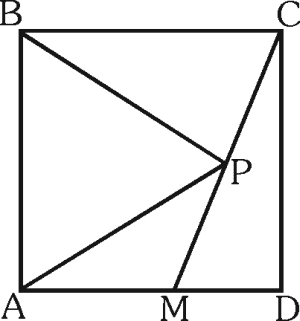
Sea ABCD un cuadrado y el triángulo ABP es equilátero, calcula m∠CMD.
A) 15°
B) 45°
C) 60°
D) 75°
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 10 :
Si el volumen de un cilindro recto es el doble del volumen de un cono recto, tal que los radios de sus respectivas bases tienen igual medida; calcula la relación entre las alturas del cilindro y cono, respectivamente.
a) 1/4
b) 2/3
c) 3/4
d) 1
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 11 :
Se tiene un triángulo rectángulo isósceles y un cuadrado, cuyas regiones son equivalentes. Calcule la relación de la hipotenusa y la diagonal del cuadrado.
A) 1
B) √2
C) 2√2
D) 3
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 12 :
En un trapecio se cumple que el segmento que une los puntos medios de las diagonales y la mediana están en relación de 3 a 5. Calcule la relación de sus bases.
A) 1
B) 2
C) 3
D) 4
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 13 :
Del gráfico mostrado, calcule “x” si AF=AC y BD=BC.
A) 20°
B) 24°
C) 26°
D) 28°
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 14 :
Del gráfico mostrado, calcule CD si AC=24 μ, BC=8 μ y O es centro.
A) √2
B) 2√2
C) 3√2
D) 4√2
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 15 :
En el gráfico mostrado, AM=MC, BL=LM, AΔBLE=8μ2 , 2(EC)=3(BE) ; calcule AΔABC.
A) 80
B) 70
C) 65
D) 64
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 16 :
En el gráfico, AH=3, AP=2, AL=AM+2; calcule AM.
A) 2,5
B) 3
C) 4
D) 4,5
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 17 :
Se tiene un cilindro de radio 6 y generatriz 30 que contiene cierto líquido. Se desea vaciar el líquido en vasos de forma de tronco de cono de radio menor 2, radio mayor 4 y altura 8, con la condición de que solo los vasos se llenan hasta sus tres cuartas partes. Calcula la cantidad de vasos empleados aproximadamente.
A) 18
B) 19
C) 20
D) 21
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 18 :
Una cometa es soltada tal que la cuerda que sostiene a la cometa se estira 50 m. Si el ángulo de inclinación que forma la cuerda con la horizontal es 37°, calcule a qué altura se encuentra la cometa.
A) 10
B) 20
C) 30
D) 40
RESOLUCIÓN :
Rpta. : "C"
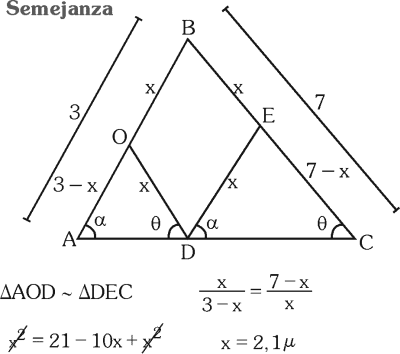
PREGUNTA 19 :
A) 2 μ
B) 2,1 μ
C) 2,5 μ
D) 3 μ
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 20 :
A) 3 μ
B) 4 μ
C) 7 μ
D) 8 μ
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 21 :
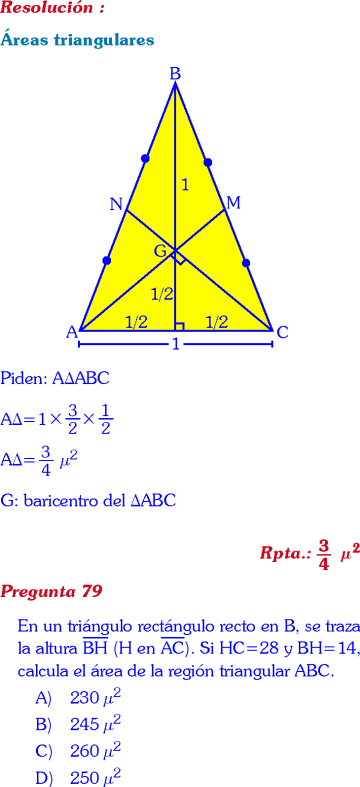
En un triángulo isósceles ABC, se trazan las medianas AM y CN perpendiculares. Si AC=1 y AB=BC, calcula el área de la región triangular ABC.
A) 2 μ²
B) 3/2 μ²
C) 3/4 μ²
D) 3/8 μ²
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 22 :
En un triángulo rectángulo recto en B, se traza la altura BH (H en AC). Si HC=28 y BH=14, calcula el área de la región triangular ABC.
A) 230 𝑢2
B) 245 𝑢2
C) 260 𝑢2
D) 250 𝑢2
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 23 :
En un trapecio isósceles ABCD. Si AB=5, BC=4 y AD=10.
Calcule el área del trapecio.
A) 25 𝑢2
B) 26 𝑢2
C) 27 𝑢2
D) 28 𝑢2
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 24 :
Se tiene un trapecio ABCD, se traza BD de tal manera que la m∢CBD=35º, m∢BCD=110º y AD=2BC=2CD. Calcule la medida del ángulo BAD.
A) 40º
B) 45º
C) 50º
D) 55º
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 25 :
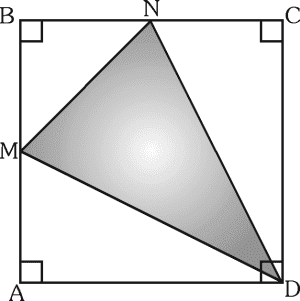
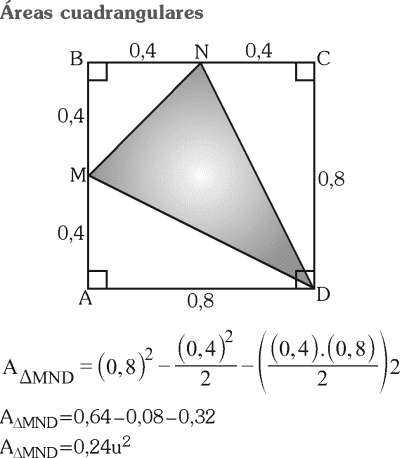
Del gráfico, si M y N son puntos medios de los segmentos AB y BC respectivamente, si AB=BC=0,8.
Calcule el área de la región triangular MND
A) 0,24u²
B) 0,25u²
C) 0,26u²
D) 0,18u²
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 26 :
Se tiene un triángulo equilátero de área 3√3u2 . Determine el área de la región circular circunscrita a dicho triángulo
A) 2𝛑
B) 3𝛑
C) 6𝛑
D) 4𝛑
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 27 :
Se tiene dos esferas cuya relación de volúmenes es de 1 a 2, si el radio de la menor es ∛16 .
Calcule el volumen de la esfera mayor.
A) 143𝛑/3
B) 196𝛑/3
C) 129𝛑/3
D) 128𝛑/3
RESOLUCIÓN :
Rpta. : "D"
**