GEOMETRÍA EJEMPLOS RESUELTOS CATÓLICA
PREGUNTA 1 :
A) 30°
B) 45°
C) 75°
D) 80°
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 2 :
Del grafico; calcule el perímetro de la región sombreada ABCD: Cuando; M, N, P y Q son puntos medios.
A) 4 + 𝛑
B) 4 + 𝛑/2
C) 4 + 2𝛑
D) 4 + 3𝛑/2
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 3 :
Se tienen cuatro ángulos consecutivos AOB, BOC, COD y DOE tal que A, O, E son colineales, se sabe que los cuatro ángulos se encuentran en progresión aritmética y además la medida del ángulo mayor es el doble de la medida del ángulo menor. Calcule la diferencia de los dos ángulos intermedios en medida.
A) 5º
B) 8º
C) 10º
D) 12º
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 4 :
Del gráfico; el diámetro, AC mide 32μ, BO=4. Si FB⊥AC, calcule el perímetro de la región triangular AFC.
A) 4√6 + 5√10 + 32
B) 8√6 + 7√10 + 32
C) 8√6 + 8√10 + 32
D) 5√3 + 7√8 + 36
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 5 :
Del gráfico, AEFD es un cuadrado, ABCD es un rectángulo, M es punto medio y AM=1. Calcule el área de la región EBCF.
A) 4 u2
B) 6 u2
C) 8 u2
D) 10 u2
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 6 :
A) 120/7 u2
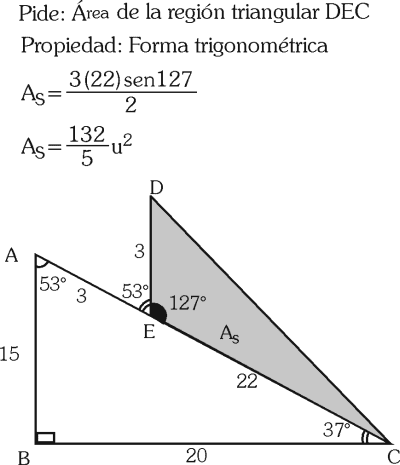
B) 132/5 u2
C) 140/9 u2
D) 135/8 u2
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 7 :
Del gráfico, O y O1 son centros; A, B, C, D y E son puntos de tangencia. Calcule el área de la región sombreada.
A) 12√2 u2
B) 18√2 u2
C) 22√2 u2
D) 24√2 u2
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 8 :
A) √5 – √(14/3)
B) √5 – √5/3
C) √7 – √(14/3)
D) √6 – √(14/3)
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 9 :
Calcule el área de la región sombreada si “O” y “O1” son centros. Si AB =2u , EF=1u
A) (√2 – 𝛑/6) u2
B) (√7 – 𝛑/3) u2
C) (√2 – 𝛑/5)/5 u2
D) (√3 – 𝛑/6)/4 u2
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 10 :
En un prisma hexagonal regular ABCDEF-GHIJKL, se inscribe una pirámide regular tal que su base coincide con la base ABCDEF y su vértice coincide con el centro de la base superior. La arista lateral de la pirámide mide 20 u y forma con el plano de la base un ángulo cuya medida es 60º. Calcule el volumen del Prisma.
A) 3 500 u3
B) 4 200 u3
C) 4 500 u3
D) 5 200 u3
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 11 :
A) 2
B) 3
C) 4
D) 5
RESOLUCIÓN :
Rpta. : "A"
Teorema de Pitágoras
En todo triángulo rectángulo, se verifica el teorema de Pitágoras: b²=a²+c²
Esto quiere decir que existe una relación fija entre los lados de un triángulo rectángulo: el cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de los catetos.
Este teorema se suele emplear cuando se conocen solo dos de las longitudes de los lados de un triángulo rectángulo y se quiere determinar la longitud del tercer lado.
Una consecuencia muy útil del teorema de Pitágoras es el siguiente resultado:
Al trazar la altura relativa a la hipotenusa, esta queda dividida en dos segmentos de longitudes m y n de modo que: h2=m.n
problemas.
Por ejemplo, en un paralelogramo, las diagonales se cortan en su punto medio; en un rombo, las diagonales son perpendiculares; en un cuadrado de lado a, se verifica que su diagonal mide 2 a ; entre otras.
Ejemplo
Con un galón de pintura, se pueden pintar 30m². Se quieren pintar las paredes de un cuarto, cuyas dimensiones son de 20m de largo, 10m de ancho y 3m de altura. El cuarto tiene una puerta de 2m×1,5m, dos ventanas de 5m×2m y una ventana de 3,5m×2m.
¿Cuántos galones de pintura se necesitan para pintar las paredes?
A. 4
B. 5
C. 6
D. 7