ÁLGEBRA SIMULACRO EXAMEN BECA 18 PRONABEC ADMISIÓN UNIVERSIDAD PRUEBA ÚNICA NACIONAL RESUELTA PDF

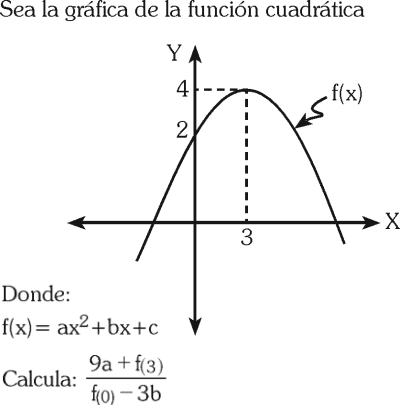
PREGUNTA 1 :

A) –2

B) –1

C) 2

D) 1

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 2 :

El costo de un carro al inicio de un año es S/ 32 000, si tiene una devaluación de S/ 650 por cada año. Hallar el costo que tendrá dentro de 17 años.

A) S/ 20 900

B) S/ 25 900

C) S/ 29 950

D) S/ 20 950

RESOLUCIÓN :

Planteo de ecuaciones

Datos: Costo inicial=32 000

Devaluación=650 (por año)

Luego, para un tiempo de 17 años:

Costo final=32 000 – 650(17)

Costo final=S/ 20 950

Rpta. : "D"

PREGUNTA 3 :

Si f(0) = 1; f(1) = 0 ; f(– 1) = 6

Calcula f(2) siendo “f” una función cuadrática.

a) – 1

b) 2

c) 3

d) – 5

RESOLUCIÓN :

Funciones

Como “f” es cuadrática

f(x) = ax²+bx+c

Del dato

f(0) = 1 → c = 1 f(1) = 0

→ a+b+c = 0

a+b = – 1 ... (α)

f( – 1) = 6 → a – b+c=6

→ a – b=5 ... (β)

De “α” y “β”; a = 2 ∧ b = – 3

∴ f(x) = 2x² – 3x+1; luego, f(2) = 3.

Rpta. : "C"

PREGUNTA 4 :

A) – 7

B) – 3

C) 0

D) 3

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 5 :

A) 1

B) x

C) x³

D) x²

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 6 :

Siendo “f” una función lineal; además

f(2) = 0 ∧ f(1) = – 3, halla f(x).

a) f(x) = 3x+6

b) f(x) = – 3x+6

c) f(x) = – 3x

d) f(x) = 3x – 6

RESOLUCIÓN :

Funciones

Como “f” es lineal f(x) = ax+b.

Luego, del dato tenemos

x → f(2) = 2a+b → 2a+b = 0

x = 1 → f(1) = a+b → a+b = – 3

al resolver

a = 3 ∧ b = – 6

∴ f(x) = 3x – 6

Rpta. : "D"

PREGUNTA 7 :

Dos automóviles parten simultáneamente de un determinado punto. El primero recorre 10 km empleando una velocidad de 5 km/h; el segundo, utilizando el mismo tiempo que el primero, recorre 12 km a “y” km/h. Calcula “y”.

a) 5 km/h

b) 7 km/h

c) 6 km/h

d) 5,5 km/h

RESOLUCIÓN :

Planteo de ecuaciones

1°.

d = 10 km

v = 5 km/h

d = v.t

10 = 5t

t = 2 horas

2°.

d = 12 km

v = y

d = v.t

12 = y(2)

y = 6 km/h

Rpta. : "C"

PREGUNTA 8 :

a) 47

b) 48

c) 49

d) 50

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 9 :

Se tiene un rectángulo cuya área es 36m² y su perímetro 30m. Calcule la diferencia entre el mayor y menor de los lados.

A) 9

B) 10

C) 11

D) 12

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 10 :

Dado el polinomio

P(x;y)≡ x³+y³+3(x²y+xy²)

Halle el valor de :

P(b −1;3 − b) − P(−1;1)

A) 1

B) 4

C) 8

D) 16

RESOLUCIÓN :

Polinomios Valor numérico Del polinomio

P(x;y)≡ x³+y³+3(x²y+xy²)

P(x;y) ≡ (x+y)³

Se pide P(b −1;3 − b) − P(−1;1)

= (b −1+3 −b)³−(−1+1)³

= 2³− 0=8

Rpta. : "B"

PREGUNTA 11 :

Al dividir el polinomio P(x)≡x⁴+1 entre el polinomio x²−1, se obtiene un cociente Q(x) y residuo R(x). Calcule el equivalente de 3Q(x) − R(x).

A) 3x²−2

B) 3x²+1

C) 3x²

D) 3x²−1

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 12 :

Factorice

P(a;b)≡4−a²−b²+2ab

A) (a+b+2)(a − b − 2)

B) (a − b+2)(b − a+2)

C) (a − b+2)(a+b − 2)

D) (a+b − 2)(b+a − 2)

RESOLUCIÓN :

Factorización Diferencia de cuadrados

P(a;b)≡4−(a²−2ab+b²)

≡ 4 − (a − b)²

≡ (2+a − b)(2 − a+b)

Rpta. : "B"

PREGUNTA 13 :

De la igualdad

halle A+B+C.

A) − 3

B) − 2

C) 1

D) 3

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 14 :

Resuelva

A) CS={− 2}

B) CS={1}

C) CS={2}

D) CS={−1}

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 15 :

Un camión transporta 420 cajas. Al pasar por un controlador de peso este excedía el peso límite en 65 kg; al retirar 12 cajas el nuevo peso está 19 kg debajo del límite. Halle el peso de cada caja si todas pesan igual.

A) 10

B) 12

C) 9

D) 7

RESOLUCIÓN :