RAZONAMIENTO MATEMÁTICO UNI EJERCICIOS RESUELTOS PDF
PREGUNTA 1 :
¿Qué figura es discordante?
RESOLUCIÓN :
Cada figura tiene 4 regiones simples a excepción de la alternativa C, que tiene 3 regiones simples.
Rpta. : "B"
PREGUNTA 2 :
En la malla 5×5 mostrada en la figura, 15 celdas contienen X y 10 celdas están vacías. Se pide determinar el mínimo número de X que deben moverse a las celdas vacías de modo que cada fila y cada columna contenga exactamente tres X.
A) 4
B) 2
C) 3
D) 1
E) 5
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 3 :
Halle el término que continua la sucesión:
1 ; 4/9 ; 3/14 ; 8/65 ; 5/63 ; a/b ; …
Dé como respuesta a+b.
A) 229
B) 249
C) 220
D) 228
E) 225
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 4 :
Las tres primeras figuras de un patrón son mostradas a continuación. Halle el número de cuadrados que componen la figura 25.
A) 51
B) 45
C) 43
D) 55
E) 47
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 5 :
Halle el valor de X+Y en:
A) 30
B) 40
C) 48
D) 32
E) 28
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 6 :
A) 7/8
B) 3/2
C) 3/4
D) 4/3
E) 5/6
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 7 :
Manuel rinde un examen que tiene en su primera parte 30 preguntas y en la segunda parte, 50. Él contestó exactamente el 70% de las preguntas de la primera parte de forma correcta, asimismo el 40% de las preguntas de la segunda parte en forma correcta. El porcentaje de todas las preguntas que Manuel contestó en forma correcta es aproximadamente
A) 53
B) 60
C) 57
D) 51
E) 58
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 8 :
La siguiente tabla de frecuencias obtiene la cantidad de votos a favor y en contra acerca de un referéndum en una población de 710 personas agrupadas por rango de edad en años. Señale la alternativa que presenta la secuencia correcta después de determinar si la proposición es verdadera (V) o falsa (F).
I. El porcentaje de personas total que están a favor del referéndum y cuya edad es al menos de 61 años es del 36%.
II. El porcentaje de personas que están en contra y en el rango de 26 a 60 años es de 22% redondeado al entero más próximo.
III. Si los votos válidos excluyen a los indecisos entonces el porcentaje de los votantes de 18 a 25 años es del 21 % de los votos válidos aproximadamente.
A) FFF
B) FVF
C) VVV
D) FVV
E) VFV
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 9 :
Dados los operadores:
a♥b=ab+ba; (a+b) par
a♥b=ab; (a+b) impar
Halle el valor de E= (2♥1)♥(1♥3)
A) 30
B) 36
C) 32
D) 28
E) 26
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 10 :
La siguiente gráfica muestra el número de postulantes (en cientos) a una universidad durante el periodo 2011 a 2021. En base a ello, señale la alternativa que presenta la secuencia correcta después de determinar si la proposición es verdadera (V) o falsa (F).
I. El porcentaje de disminución de postulantes del año 2019 al 2020 es del 37%, aproximadamente.
II. De acuerdo al gráfico solo hay dos periodos anuales cuando el número de postulantes ha aumentado.
III. El promedio de postulantes entre los años 2011 y 2015 es de 3960.
A) FFF
B) FVV
C) FVF
D) VVV
E) VFV
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 11 :
Se tiene la siguiente tabla infinita de números, donde los números en cada fila forman una sucesión aritmética y los de cada columna también forman una sucesión aritmética. Se pide determinar el número en la fila 50 y columna 40.
A) 4090
B) 3260
C) 3480
D) 3680
E) 3800
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 12 :
Se desea conocer la cantidad de partidos que ganó, una selección sudamericana cualquiera, en las eliminatorias donde participaron todas las selecciones, con la información brindada:
1. La cantidad total de puntos que obtuvo fue 31.
2. Ganó de local tanto como de visitante y no ganó dos veces a una misma selección.
A) Falta información.
B) Ambas informaciones son necesarias.
C) Cada información por separado es suficiente.
D) Solo la primera información es necesaria.
E) Solo la segunda información es necesaria.
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 13 :
Se desea conocer cuántas vocales tiene el primer nombre de un postulante, que tiene ocho letras, con la información brindada:
1. Las consonantes y las vocales están intercaladas.
2. La cantidad de consonantes excede al de vocales en dos.
A) Cada información por separado es suficiente.
B) Solo es suficiente la segunda información.
C) Solo es suficiente la primera información.
D) Son necesarias ambas informaciones.
E) Falta información.
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 14 :
Calcule el mayor número de dos dígitos tal que si invertimos los dígitos (decenas en unidades y unidades en decenas) el nuevo número es 75% mayor al número original.
Indique como respuesta la suma de los dígitos del número.
A) 3
B) 9
C) 6
D) 12
E) 10
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 15 :
Dados los operadores definidos mediante:
21▲22=6
32▲13=10
12▲31=4
23▲32=17
13▼11=2
24▼21=2
39▼12=4
79▼22=4
Halle el valor de:
E={99▼[18▲30]}
A) 9
B) 17
C) 5
D) 39
E) 44
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 16 :
Se desea conocer las dimensiones a, b y c de un triángulo, con la información brindada:
1. Es un triángulo equilátero de área 𝔸 conocida.
2. Es un triángulo rectángulo e isósceles de perímetro P conocido.
A) Solo la segunda información es necesaria.
B) Falta información.
C) Solo la primera información es necesaria.
D) Cada información por separado es suficiente.
E) Ambas informaciones son necesarias.
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 17 :
Antonio, Eduardo, Julio y Víctor fueron a cenar en compañía de sus esposas y cada uno se sentó junto a su esposa. En el restaurante ocuparon una mesa redonda y se sentaron de modo que cumplían las siguientes condiciones:
✎ Frente a Antonio se sentaba Julio.
✎ A la derecha de la esposa de Antonio se sentaba Eduardo.
✎ No había dos hombres juntos.
Con estas condiciones, quién se sentaba entre Antonio y Víctor.
A) Esposa de Antonio
B) Esposa de Eduardo
C) Julio
D) Esposa de Julio
E) Esposa de Víctor
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 18 :
Deseamos conocer si el área del círculo X es mayor que el área del círculo Y.
I. El radio del círculo X es menor que el radio del círculo Y.
II. La longitud de la circunferencia del círculo X es mayor que la longitud de la circunferencia del círculo Z.
Con la información brindada, selecciona la mejor respuesta:
A) Se necesita usar tanto I y II para resolver el problema.
B) I por sí solo es suficiente para resolver el problema.
C) II por sí solo es suficiente para resolver el problema.
D) Con cada hecho en forma independiente se puede resolver el problema.
E) Aparte de I y II se necesita información adicional para resolver el problema.
RESOLUCIÓN :
I. Radio de x<Radio de y → Con dicha información sí se puede determinar qué área de las dos es la mayor.
II. 2pRx > 2pRz → Aquí menciona al círculo z que no tiene que ver con lo solicitado.
Por lo tanto, para obtener lo pedido es suficiente I.
Rpta. : "B"
PREGUNTA 19 :
Dado el cubo: ¿Cuál de los siguientes cubos es discordante con la figura dada?
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 20 :
Sea el evento de extracción secuencial de bolillas sin reposición. Se desea conocer la probabilidad de sacar la cuarta bolilla de color rojo de una urna que contiene bolillas de cuatro colores: rojo, azul, negro y blanco, cuyas cantidades son 3; 1; 1 y 1, respectivamente, con la información brindada:
1. En las primeras tres extracciones, había dos bolillas de igual color.
2. Las tres primeras bolillas extraídas fueron de colores iguales.
A) Solo la primera información es necesaria.
B) Solo la segunda información es necesaria.
C) Cada información por separado es suficiente.
D) Ambas informaciones son necesarias.
E) Falta información.
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 21 :
Cuando se dobla el cubo de la figura, establecer cuál(es) de los sólidos 1 a 5 se producen:
A) 1, 3
B) 4
C) 1, 2
D) 4, 5
E) 3, 4
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 22 :
Seis dados están colocados en el piso como se muestra. En cada dado el 1 es opuesto al 6, el 2 al 5 y el 3 al 4. Halle la máxima suma posible de los números en las 21 caras visibles.
A) 74
B) 78
C) 80
D) 89
E) 76
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 23 :
Sabiendo que a y b son enteros positivos. Determine la cantidad de posibles pares (a; b) que cumplen a³+2ab=2013
A) 5
B) 3
C) 6
D) 2
E) 4
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 24 :
Daniel compra dos tipos de juguetes: carros de carrera y algunos helicópteros. Paga un total de S/201 soles. Compra juguetes enteros y no hay fracciones de ninguno de ellos. Cada carrito costó S/.19 soles y cada helicóptero costó S/.17 soles. Calcule el número total de juguetes que compró Daniel.
A) 11
B) 10
C) 12
D) 13
E) 9
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 25 :
El rango de una lista de números es la diferencia entre el mayor número y el menor número de la lista. Por ejemplo el rango de la lista 1, 5, 1, 6, 3 el rango es 6 – 1= 5 ya que 6 es el mayor y 1 el menor. Si la lista 11, 5, a, 13, 10 tiene como rango 12. Determine la suma de todos los posibles valores que tiene a.
A) 20
B) 16
C) 18
D) 21
E) 17
RESOLUCIÓN :
Datos:
rango = mayor valor – menor valor =12
Tenemos 11; 5; a; 13; 10
• Si a es el mayor, entonces en 5; 10; 11; 13; a rango=a – 5= 12 ⇒ a=17
• Si a es el menor, entonces en a; 5; 10; 11; 13 rango=13– a= 12 ⇒ a=1
Por lo tanto, la suma de valores de a es 17 +1= 18
Rpta. : "C"
PREGUNTA 26 :
En la siguiente figura, el arreglo de la izquierda es formado de acuerdo a una determinada regla que es válida para las filas/columnas. Aplicar el mismo criterio para el arreglo de la derecha y establezca el valor que debe ir en el casillero vacío.
A) 1
B) 4
C) 3
D) 2
E) 5
RESOLUCIÓN :
En cada columna la casilla inferior menos la casilla central, dividido entre 2, da la casilla superior.
Rpta. : "C"
PREGUNTA 27 :
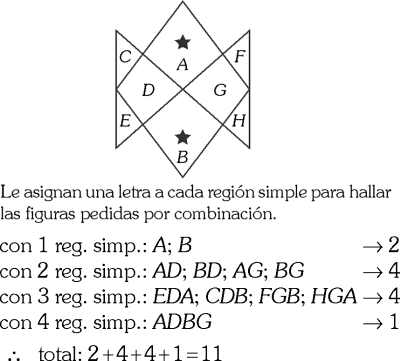
¿Cuántos cuadriláteros pueden contarse en la siguiente figura que contengan al menos una estrella negra?
A) 6
B) 7
C) 11
D) 10
E) 5
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 28 :
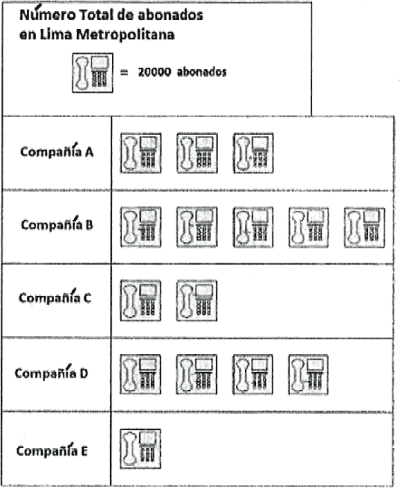
El siguiente pictograma representa el total de abonados que tienen diversas compañías telefónicas en Lima. En base a ello señale la alternativa que presenta la secuencia correcta, después de determinar si la proposición es verdadera (V) o falsa (F).
I. Del total de abonados en Lima, el porcentaje de más abonados que tiene la compañía A con respecto a la compañía C es del 50% aproximadamente.
II. Las compañías A y B registran al 60 % de todos los abonados.
III. Las compañías A, C y E en conjunto tienen el 50% de todos los abonados.
A) VFF
B) VVF
C) FVF
D) FVV
E) FFF
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 29 :
¿Qué figura continúa?
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 30 :
¿Qué figura continúa?
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 31 :
Se define a@b = a + b –100.
Determinar si cada proposición es verdadera (V) o falsa (F).
I. El elemento neutro en esta operación es 100.
II. El elemento inverso de 100 es 200.
III. Para todo a, b, c se cumple que
(a@b)@c =a@(b@c)
A) VFF
B) VVF
C) FFV
D) VVV
E) VFV
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 32 :
Se dan las siguientes proposiciones:
B: Bernardo ingresó a la FIEE
C: Carlos ingresó a la FIEE
D: David ingresó a la FIEE
Se pide formalizar la siguiente proposición:
“Carlos ingresó a la FIEE si es que David no lo hizo, pero si David ingresa entonces Bernardo no ingresará”
A) (∼ D → C) ∨ (D → ∼ B)
B) (D → ∼ C) ∧ (B → ∼ D)
C) (C → ∼ D) ∧ (∼ B → ∼ D)
D) (∼ D → C) ∧ (D → ∼ B)
E) (C → ∼ D) ∨ (D → ∼ B)
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 33 :
Halle el valor de x en
A) 15
B) 34
C) 18
D) 28
E) 13
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 34 :
El siguiente pictograma representa el número de viviendas construidas en Lima durante los años del 2018 al 2020. En base a ello, señale la alternativa que presenta la secuencia correcta después de determinar si la proposición es verdadera (V) o falsa (F).
I. El porcentaje de disminución de viviendas del año 2018 al 2020 es del 28,67% aproximadamente.
II. El total de viviendas construidas entre los años 2018 a 2020 es de 320 000.
III. El número de viviendas construido el 2020 es la mitad de las construidas el 2018.
A) FFF
B) FVV
C) FVF
D) FFV
E) VFV
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 35 :
En este juego suponga que se tienen n platos que están igualmente espaciados en una mesa circular. Lenin desea ubicar un regalo en cada uno de k platos, de forma que los platos vecinos no tengan regalo. Definimos a f(n, k) como el número de formas en las cuales podemos colocar los regalos y por ejemplo f(6;3) = 2 como se muestra en la figura. Se pide determinar f(7;3).
A) 5
B) 8
C) 10
D) 6
E) 7
RESOLUCIÓN :
Rpta. : "E"
