GEOMETRÍA UNI EJERCICIOS RESUELTOS PDF
PREGUNTA 1 :
Los puntos F, M, A y G son colineales y consecutivos.
Si
FG= 27
FM=x – y
MA=x+y
AG=2y – x
Calcular el menor valor de x sabiendo que el valor de y es entero.
A) 11
B) 9
C) 27
D) 1
E) 13
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 2 :
Se desea diseñar un molde como se muestra en la figura siguiente:
Sobre el diámetro de un semicírculo de centro O, se toman segmentos AB, BO, OD y DE de igual longitud, los cuales son diámetros de las semicircunferencias F, G, H e I. Si el diámetro del semicírculo mayor es 2R entonces la medida de la longitud total de dichas semicircunferencias menores es
A) 2𝛑R
B) 𝛑R/2
C) 𝛑R2
D) 𝛑R
E) 3𝛑R/4
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 3 :
De la figura mostrada:
se tiene que BD es bisectriz del ángulo ABE y BE es bisectriz del ángulo ABC.
Si x+y+z = 70, determine el valor de xy+z
A) 204
B) 100
C) 202
D) 200
E) 102
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 4 :
Los lados de un triángulo ABC inscrito en una circunferencia miden:
AB= 12, AC= 10 y BC=8
Por B se traza una recta tangente a la circunferencia que corta a la prolongación del lado AC en M. Redondee el valor de BM.
A) 27
B) 12
C) 14
D) 10
E) 9
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 5 :
Un hacendado compra un terreno en forma de hexágono regular de área total 18√3 m². Luego se cerca el terreno que se encuentra dentro del polígono que se obtiene al unir los puntos medios de los lados consecutivos del terreno original. Una vez cercado el terreno, contrata a un pintor para pintar la parte exterior del cerco que tiene 2 m de altura. Sabiendo que 1 galón de pintura alcanza para 4 m², determine la cantidad de galones que se necesitan para pintar lo solicitado por el hacendado.
A) 3√3
B) 18
C) 9
D) 15
E) 18√3
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 6 :
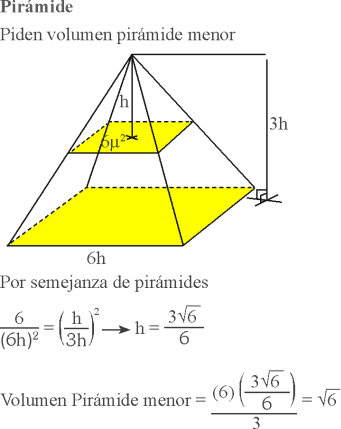
Dada una pirámide de base cuadrada, se traza un plano paralelo a la base consiguiéndose así una pirámide menor tal que su base cortante tiene área de 6 unidades cuadradas. Si la relación de alturas entre las pirámides es de 1 a 3 y el lado de la base de la pirámide mayor es el doble de su altura, determine el volumen de la pirámide menor.
A) 5√6/3
B) 8 √6/3
C) 2√6/3
D) √6
E) 4√6/3
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 7 :
Determine el volumen (en cm³) de un tronco de prisma recto cuyas bases son un triángulo equilátero FED y un triángulo rectángulo isósceles ABC. Además, una cara lateral es un rectángulo de lados 6√2 cm y 12 cm, tal que las aristas laterales son mayores que las aristas de las bases.
A) 224
B) 242
C) 262
D) 252
E) 432
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 8 :
Se ubican los puntos A y B, uno a cada lado de un plano 𝛑, de modo que la distancia de estos hacia el plano están en la relación de 1 a 3, respectivamente. Si la proyección del segmento AB sobre el plano mide 24 unidades y el ángulo que forma AB con el plano 𝛑 es de 53°, determine AB (en unidades).
A) 40
B) 30
C) 20
D) 15
E) 60
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 9 :
El desarrollo de la superficie lateral de un cono de revolución es un sector circular de radio 10 cm y un ángulo central de medida 216°. Determine el volumen del cono original (en cm³).
A) 92𝛑
B) 96𝛑
C) 76𝛑
D) 128𝛑
E) 81𝛑
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 10 :
Un tetraedro regular se proyecta sobre un plano perpendicular a una arista. Si la longitud de la arista del tetraedro es 8, determine el área de dicha proyección.
A) 16√2
B) 8√2
C) 12√2
D) 16√3
E) 9√2
RESOLUCIÓN :
Rpta. : "A"
