RAZONAMIENTO MATEMÁTICO RESUELTO DE INGRESO UNIVERSIDAD

PREGUNTA 1 :

Jael y Ana Lucía gastaron en la compra de libros 360 soles entre ambos, si Jael gastó el cuádruplo que Ana Lucía, aumentado en 20 soles, ¿cuál es la diferencia del dinero gastado por ambos? 

A) 214 

B) 208 

C) 224 

D) 258 

E) 178 

RESOLUCIÓN :

Ana gasta: x

Jael : 4x+20 

Por condición: 

x+4x+20=360 

⇒ x=68 

diferencia de lo gastado por ambos: 

(4×68+20)–68=224 

Rpta. : "C"

PREGUNTA 2 :

Calcula el valor de x en la siguiente distribución: 

A) 80 

B) 6 

C) 10 

D) 40 

E) 7 

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 3 :

En la figura mostrada ABCD es un cuadrado, siendo E, F, G, H, puntos medios. Halla la diferencia entre el número total de triángulos y cuadrados. 

A) 12 

B) 6 

C) 7 

D) 18 

E) 8

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 4 :

En el 2005, la edad de mi padre era 9 veces mi edad; en el 2010, la edad de mi padre era el cuádruplo de mi edad. ¿Cuál es la edad actual de mi padre, si estamos en el 2017? 

A) 38 

B) 48 

C) 39 

D) 51 

E) 40 

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 5 :

Determina el número que continúa en la siguiente sucesión: 

–3 ; 0 ; 0 ; 0 ; 5 ; 22 ; ... 

A) 60 

B) 56 

C) 48 

D) 58 

E) 42

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 6 :  

¿Cuántas filas tendrá el arreglo triangular, formado por 120 monedas? 

a) 14 

b) 20 

c) 16 

d) 15 

e) 18 

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 7 :  

¿Qué hora marcan las manecillas del reloj que muestra la figura? 

a) 9 h 36 min 

b) 9 h 38 min 

c) 9 h 39 min 

d) 9 h 37 min 

e) 9 h 35 min 

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 8 :

Un alambre de L cm de longitud, se divide mediante un corte en dos partes de igual longitud, luego en cada parte se realizan nuevos cortes y se obtiene un número exacto de trozos; en la primera, 7 cortes de 2 cm de largo; y en la segunda, 3 cortes de 4 cm de largo. Si los cortes se hicieron de uno en uno y no se pudo doblar el alambre en ningún momento, halle la longitud del alambre. 

A) 34 cm 

B) 30 cm 

C) 20 cm 

D) 24 cm 

E) 32 cm 

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 9 :

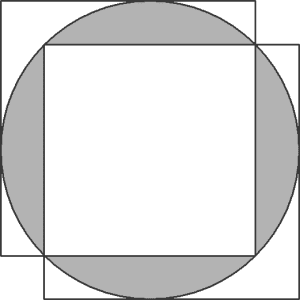
La figura muestra dos cuadrados iguales, que cubren un circulo. Si el área de la región sombreada es (9𝛑–18) cm². Halle el área de un cuadrado. 

A) 24 cm² 

B) 14 cm²

C) 20 cm²

D) 18 cm²

E) 16 cm² 

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 10 : 

El número de billetes de S/ 20 que tiene Bop es 40 veces el número de billetes de S/ 20 que tiene Pili; menos el cuadrado, del doble del número de billetes de S/ 20 que tiene Pili. ¿Cuál es la máxima cantidad de soles que podría tener Bop? 

A) 2000 

B) 2500 

C) 3000 

D) 3500 

RESOLUCIÓN :

Billetes de Abel = x 

Billetes de Boris = y 

x = 40y – (2y)²

x = – 4(y² – 10y) = 100 – 4(y – 5)²

x_MAX= 100 

Dinero de Bop = 20(100) = 2000 soles 

Rpta. : "A"

PREGUNTA 11 :

En la figura mostrada, MNPQ es un rectángulo y las medidas están dadas en centímetros. ¿Cuál es la menor longitud que debe recorrer la punta de un lápiz, sin separarla del papel, para dibujar dicha figura? 

A) 37 cm 

B) 39 cm 

C) 40 cm 

D) 41 cm 

E) 42 cm 

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 12 : 

En la figura ABCD es una mesa de forma rectangular, AB=80cm; BC=210 cm y M punto medio de CD. Si una hormiga se encuentra en el punto A y debe ir al punto M siguiendo la trayectoria indicada en la figura, ¿cuál es la longitud mínima, en centímetros, recorrida por la hormiga? 

A) 300 

B) 330 

C) 340 

D) 350 

RESOLUCIÓN :

En la figura se muestran los trazos que se deben realizar 

Rpta. : "D"

PREGUNTA 13 : 

De la operación mostrada, ¿por lo menos cuántas fichas numeradas deben ser cambiadas de posición para que el resultado sea el mínimo valor posible? 

A) 2 

B) 3 

C) 4 

D) 5 

RESOLUCIÓN :

En la figura se muestran las cuatro fichas que se mueven 

Rpta. : "C"

PREGUNTA 14 : 

En el mes de agosto de un cierto año hubo exactamente cinco martes, cinco miércoles y cinco jueves, ¿qué día de la semana fue 28 de agosto de dicho año? 

A) Jueves 

B) Viernes 

C) Domingo 

D) Lunes 

E) Martes 

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 15 :

Se tiene 3 engranajes A, B y C donde A con 24 dientes, está engranado con B que tiene 36 dientes y este a su vez está engranado con C que tiene 45 dientes. Si la diferencia entre el número de vueltas entre A y C es 175, ¿cuántas vueltas habría dado el engranaje B? 

A) 375 

B) 225 

C) 250 

D) 350 

E) 200

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 16 :

En una reunión, Anita, Bertha y Micaela tienen la siguiente conversación: 

I) Anita: Nací 24 años antes que Micaela y no superó los 35 años de edad 

II) Bertha: Tengo 20 años de edad y Micaela 10 años 

III) Micaela: Tengo 24 años de edad y soy menor que Bertha 

Si solo una de ellas está mintiendo, determine la suma de edades en años de Bertha y Micaela. 

A) 44 

B) 36 

C) 54 

D) 60 

E) 30 

RESOLUCIÓN :

I. Anita: Nací 24 años antes que Micaela y no supero los 35 años de edad. 

Micaela=x ; Anita=x+24 

→ V V 

II. Bertha: Tengo 20 años de edad y Micaela 10 años. 

Bertha=20; Micaela=10; Anita=34 

→ V (suponiendo)

 III. Micaela: Tengo 24 años de edad y sor menor que Bertha. 

F ∧ V ≡ F 

Se tiene: VVF 

VF (como es conjunción entonces toda una proposición es falsa) 

∴ 20+10=30 

Rpta. : "E"

PREGUNTA 17 :

En una reunión familiar donde participaron 2 padres, 2 hermanos, un tío y un sobrino. Cada uno lanzó 2 dados, obteniendo entre todos 40 puntos. Si todos excepto el tío obtuvieron el mismo puntaje cada uno, y la cantidad de personas reunidas es la mínima, ¿cuál es el mínimo puntaje que obtuvo el tío? 

A) 8 

B) 4 

C) 6 

D) 5 

E) 3 

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 18 :

Se tiene un examen de 350 preguntas de las cuales 50 son de matemática, suponiendo que a cada pregunta de matemática se da el doble de tiempo que a cada pregunta no relacionada con esta materia. ¿Cuánto se demorará un alumno en resolver las preguntas de matemática si el examen dura tres horas? 

A) 45 min 

B) 52 min 

C) 62 min 

D) 60 min 

E) 24 min 

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 19 :

Ocho amigos: Anaís, Blanca, Diana, Helga, Carlos, Ever, Franco y Guido se sientan alrededor de una mesa circular cuyos ocho asientos se encuentran distribuidos simétricamente, y se sabe que: 

– Anaís se sienta adyacente a Franco y Ever. 

– Diana no se sienta junto a Blanca. 

– Carlos se sienta al frente de Franco. 

– Helga se sienta al frente de Blanca. 

– Guido no se sienta junto a Carlos. 

¿Cuál(es) de las siguientes afirmaciones es (son) verdadera(s)? 

I) Al menos un hombre se sienta frente a una mujer. 

II) Al menos dos mujeres se sientan juntas. 

III) No hay dos mujeres que se sientan juntas.

A) Solo I 

B) Solo II 

C) Solo III 

D) I y II 

E) I y III 

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 20 :

Un turista llega a un pueblo alejado de nuestra civilización y observa en la entrada un cartel en el que se lograba leer lo siguiente:

 "Bienvenidos" 

– En total somos: 100 

– Hombres: 30 

– Mujeres: 60 

Sin embargo, el turista al querer comprobar el resultado logró contar 81. 

¿Cómo es posible esto? 

A) En dicho pueblo utilizan base 11 

B) En dicho pueblo utilizan base 6 

C) En dicho pueblo utilizan base 9 

D) En dicho pueblo utilizan base 5 

E) En dicho pueblo utilizan base 8 

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 21 :

Seis amigos eligen una ficha con numeración diferente entre seis fichas numeradas con los seis primeros números primos positivos. 

Se sabe que: 

• El número en la ficha de Carlos es igual a la semisuma de los números de las fichas de Paolo y Abel. 

• Mario tiene una ficha cuyo número es mayor que la de Luis. 

• Paolo tiene una ficha cuyo número es menor en cuatro unidades que la de Daniel. 

¿Cuánto suman los números de las fichas de Luis y Abel? 

A) 5 

B) 9 

C) 10 

D) 13 

E) 18 

RESOLUCIÓN :

Fichas: 2, 3, 5, 7, 11 y 13 

Si Paolo=3 y Daniel= 7, a Carlos no se le asigna ninguna ficha 

Luego: Paolo=7 y Daniel=11 

Entonces Abel=3, Carlos=5, Mario=13 y Luis=2. 

La suma de los números de las fichas de Luis y Abel=2+3=5 

Rpta. : "A"

PREGUNTA 22 :

Ana, Ben, Cam y Don llevan polos con una letra y un número en su espalda. Los números son 2; 4; 6 y 8, y las letras A; B; C y D. Además, se sabe que: 

– El número que va con la letra C es el doble del número de Cam. 

– La letra de Cam aparece en su nombre. 

– La dirección de Don es el número de Don menos el número de Ben. 

– El número de Ana es la dirección de Don. 

– La posición de la letra de B en en el alfabeto (por ejemplo C es 3) es mayor que el número de Ben. 

¿Cuál es el número y la letra de Ana? 

A) 8; A 

B) 2; B 

C) 6; B 

D) 6; A 

E) 4; B 

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 23 :

Las edades en años de Abel, Belinda, Claudio, Doris, Eleazar, son números consecutivos. Todos son mayores de 13 años, pero menores de 40 años, siendo las edades de las 2 mujeres números primos que corresponden a la mayor y menor edad de todos. Calcule la suma de edades en años, de Abel, Claudio y de Eleazar. 

A) 93 

B) 75 

C) 45 

D) 54 

E) 63 

RESOLUCIÓN :

B o D     19 (Primo) 

    A         20 

    C         21 

    E         22 

D o B     23 (Primo) 

Piden: 20+21+22=63 

Rpta. : "E"

PREGUNTA 24 :

Halle la suma de cifras del resultado al operar:  

A) 266 

B) 274 

C) 272 

D) 270 

E) 268 

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 25 :

Paloma tiene en su tienda entre 336 y 342 mecheros que no puede guardar en cajas del mismo número, salvo que los guarde todos juntos o de uno en uno. ¿Cuántos mecheros tiene exactamente Paloma en su tienda? 

A) 341 

B) 339 

C) 337 

D) 340 

E) 338 

RESOLUCIÓN : 

Número de palomas: N 

336 <N <342 

N={337, 338, 339, 340, 341} 

Como mencionan que no se pueden guardar en cajas del mismo número, podemos concluir que debe ser una cantidad prima (número primo), por lo que el único número que cumple es 337.

Rpta. : "C"

PREGUNTA 26 :

¿Cuál es la menor longitud que debe recorrer la punta de un lápiz para realizar el dibujo rectangular sin separar la punta del lápiz del papel?

A) 44 cm 

B) 47 cm 

C) 43 cm 

D) 45 cm 

E) 40 cm

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 27 : 

Un cuadrado se divide en cuatro cuadraditos. Uno de los cuadraditos se divide en otros cuatro cuadraditos y así sucesivamente. Después de 69 particiones. ¿Cuántos cuadrados se contabilizan en total? 

a) 226 

b) 317 

c) 327 

d) 387 

e) 277 

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 28 :

Se distribuyen tres grupos de igual número de fichas numeradas. Si los números del primer grupo de fichas suman 37 puntos; del segundo, 35; del tercero, 24 y si en total hay 4 fichas numeradas con el 11, 4 fichas numeradas con las 12 y 4 fichas numeradas con el 1, entonces el tercer grupo tiene 

A) solo una ficha con el 12. 

B) solo una ficha con el 1. 

C) tres fichas de igual valor. 

D) dos fichas con el 1. 

E) solo una ficha con el 11. 

RESOLUCIÓN :

Con los datos se tiene: 

Primer grupo, suma= 37: 12 + 12 + 12 + 1 

Segundo grupo, suma=35: 12 + 11 + 11 + 1 

Tercer grupo, suma=24: 11 + 11 + 1 + 1. 

Luego, el tercer grupo tiene dos fichas numeradas con el 1. 

Rpta. : "D"