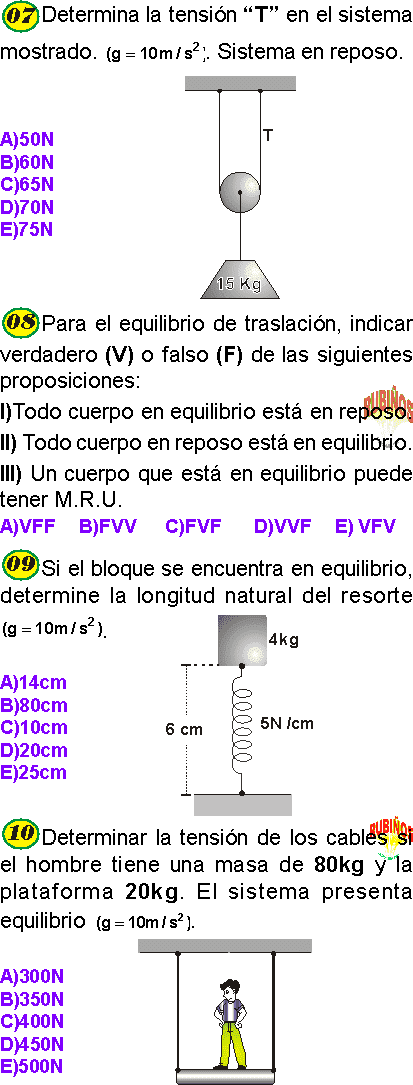
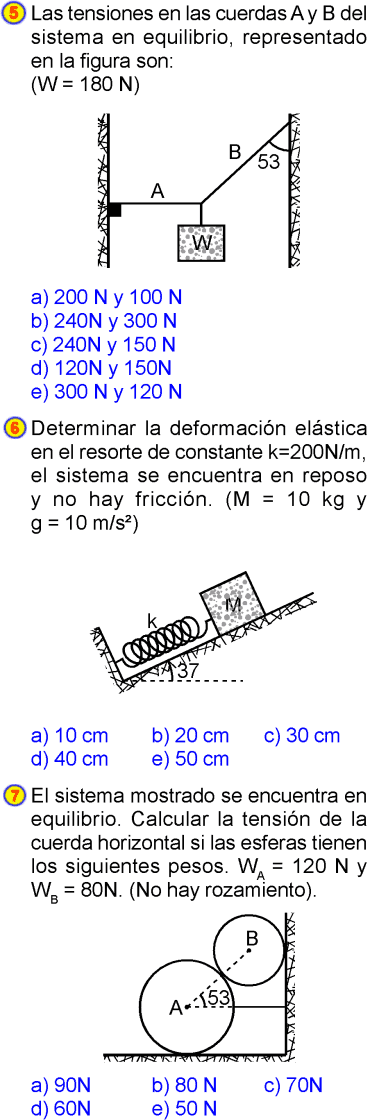
ESTÁTICA DE SECUNDARIA PROBLEMAS RESUELTOS PDF
En este capítulo estudiaremos las condiciones que deben cumplir las fuerzas que al ser aplicadas sobre un cuerpo lo mantengan en estado de equilibrio.
ESTÁTICA
Estudia las condiciones que deben cumplir los cuerpos (sistema) sobre el que actúan fuerzas para permanecer en “equilibrio mecánico”.
FUERZA
Es todo aquello capaz de provocar o acabar con un movimiento.
Toda fuerza es una magnitud vectorial ya que posee:
☛ Módulo
☛ Dirección
☛ Sentido
☛ Punto de aplicación
Unidades : Newton (N) en kg.m/s²
Medida de la fuerza : se mide con el Dinamómetro
¿ QUÉ MIDE LA FUERZA?
La fuerza mide en forma vectorial el grado de intensidad de una interacción.
PRIMERA LEY DE NEWTON (LEY DE LA INERCIA)
Basado en las observaciones de Galileo, Newton formuló lo que se conoce como la primera Ley de movimiento. "Un objeto en reposo o en movimiento con velocidad constante permanecerá indefinidamente en ese estado si ninguna fuerza actúa sobre el o si la resultante de todas las fuerzas que actúan es nula".
Es decir sólo es posible cambiar la velocidad de un objeto si una fuerza resultante actúa sobre él. Se denomina inercia a la propiedad de los cuerpos de oponerse a cualquier variación en su velocidad; el efecto de la inercia es diferente en los cuerpos con diferente masa. Es decir la masa es la cantidad de materia y está asociado directamente a la inercia que los cuerpos tienen.
TERCERA LEY DE NEWTON
LEY DE LA ACCCIÓN Y DE REACCIÓN:
“Si un cuerpo le aplica una fuerza a otro (Acción); entonces el otro le aplica una fuerza igual y en sentido contrario al primero (Reacción).”
Tener en cuenta que la acción y reacción no se anulan porque actúan en el mismo cuerpo.
No es necesario que haya contacto para que haya acción y reacción.
Si las superficies en contacto son lisas, las reacciones son perpendiculares a ellas.
Si las superficies en contacto son ásperas o hay articulaciones, las reacciones ya no son perpendiculares a las superficies en contacto.
FUERZA DE GRAVEDAD
Es aquella fuerza que mide la atracción gravitatoria que ejerce la Tierra a los cuerpos ubicados en su entorno.
La fuerza con que un cuerpo actúa sobre su apoyo o la suspensión por causa de la atracción gravitatoria se llama Peso (W).
TENSIÓN
Es aquella fuerza generada internamente en un cable, soga, barras, etc., cuando están estiradas.
El sentido de una tensión siempre indica a un corte imaginario.
COMPRESIÓN
Se presenta en los cuerpos rígidos y es aquella fuerza interna que se opone a la deformación por aplastamiento.
El sentido de una fuerza de compresión siempre se aleja de un corte imaginario
FUERZA ELÁSTICA
Es aquella fuerza que se manifiesta en el interior de los resortes cuando éstos experimentan deformaciones longitudinales elásticas.
EQUILIBRIO MECÁNICO
Es aquel estado físico en el cual un cuerpo mantiene su rapidez constante.
Existen dos casos:
EQUILIBRIO ESTÁTICO
Ocurre cuando el cuerpo se encuentra en reposo relativo.
EQUILIBRIO CINÉTICO
Ocurre cuando el cuerpo se mueve con movimiento rectilíneo uniforme.
FUERZA DE ROZAMIENTO
Es aquella fuerza que se opone al deslizamiento o posible deslizamiento de los cuerpos.
Existen dos tipos:
FUERZA DE ROZAMIENTO ESTÁTICO
Es la fuerza que se opone al intento de deslizar un cuerpo sobre una superficie debido a las mutuas asperezas entre ambos cuerpos.
FUERZA DE ROZAMIENTO CINÉTICO
Se presenta durante el deslizamiento de los cuerpos sobre las superficies ásperas
DIAGRAMA DE CUERPO LIBRE (D.C.L.)
Es un esquema donde se representan todas las fuerzas externas que actúan sobre un cuerpo, entre las fuerzas comunes tenemos:
☛ Peso (Hacia abajo)
☛ Normal (Reacción perpendicular de la superficie)
☛ Tensión (Cuerdas)
☛ Compresión (Barra)
☛ Fuerza rozamiento
Consiste en aislar imaginariamente al cuerpo en análisis de un sistema mecánico, indicando sobre él a todas las fuerzas externas que lo afectan.
PRIMERA CONDICIÓN DE EQUILIBRIO
Establece que si sobre un cuerpo la fuerza resultante es nula, se garantiza que este cuerpo se encuentra en equilibrio de traslación es decir en reposo o con M. R. U.
Cuando se tienen sólo tres fuerzas concurrentes y coplanares en el D.C.L., se puede aplicar el triángulo de fuerzas o la ley de los senos
Se establece que un cuerpo estará en equilibrio si la suma vectorial de todas las fuerzas es cero.
EQUILIBRIO DE PARTÍCULAS
Partícula es todo cuerpo (pequeño o no) en el cual podemos ignorar su movimiento de rotación.
De la primera Ley de Newton podemos deducir que si una partícula está en equilibrio sólo permanece así si la resultante de las fuerzas es nula.
Equilibrio es el estado de reposo o de movimiento con velocidad constante; físicamente son indistinguibles.
☛ Si sobre un cuerpo actúan tres fuerzas y este presenta equilibrio de traslación sin rotar, entonces dichas fuerzas deben ser no paralelas y concurrentes.
LEY DE LAMY:
En un cuerpo en equilibrio, sometido a la acción de 3 fuerzas coplanares y concurrentes, el módulo de cada fuerza es directamente proporcional al seno del ángulo que se le opone.
ESTÁTICA
La estática es la parte de la mecánica que estudia los cuerpos en estado de equilibrio sometidos a la acción de fuerzas. Ésta constituye una rama muy antigua de la ciencia, ya que algunos de sus principios fundamentales datan de la época de los egipcios y babilonios. Sin embargo, los principios en base a los cuales se ha desarrollado esta materia hasta alcanzar su forma actual se deben, principalmente, a Stevinus (1548-1620), quien fue el primero que empleó el principio del paralelogramo de fuerzas.
A lo largo de este capítulo trabajaremos, a no ser que se diga lo contrario, con una clase ideal de cuerpos físicos: los cuerpos rígidos. Un cuerpo rígido es aquel cuerpo ideal en el que la distancia entre sus partículas no se altera cuando éste se encuentra sometido a la acción de fuerzas externas, es decir, un cuerpo idealmente indeformable.
“DADME UN PUNTO DE APOYO Y MOVERÉ EL MUNDO”.
El principio de palanca es un concepto teórico estudiado en el aula, pero que se aplica diariamente a cada actividad que se realiza. Al abrir una botella de vino con un sacacorchos, al cortar un papel con una tijera, al utilizar una pinza o tenaza, etc. Sin ir más lejos, nuestro cuerpo utiliza para moverse diferentes tipos de palancas. Sin embargo, no se le da la importancia necesaria en la explicación del funcionamiento de la misma.
Ahora bien, ¿qué es una palanca?
Es una barra rígida que puede girar en torno a un punto de apoyo fijo. La longitud de la palanca entre el punto de apoyo y el punto de aplicación de la resistencia se llama brazo de resistencia y la longitud entre el punto de apoyo y el punto de aplicación de la fuerza se llama brazo de fuerza.
La función usual de una palanca es multiplicar una fuerza, es decir, que la pequeña fuerza aplicada en un extremo de una palanca a gran distancia del punto de apoyo, produzca una fuerza mayor que opere a una distancia más corta del punto de apoyo en el otro.
El empleo de la palanca está documentado desde el tercer milenio a.n.e. en sellos cilíndricos de Mesopotamia. En un manuscrito antiguo aparece la famosa cita atribuida a Arquímedes: “Dadme un punto de apoyo y moveré el mundo”.
EQUILIBRIO MECÁNICO
Se dice que un cuerpo se encuentra en equilibrio mecánico cuando su estado de movimiento como conjunto, respecto de cierto sistema de referencia, no cambia en el tiempo.
Se distinguen dos clases de equilibrio: equilibrio estático y equilibrio cinético. Se dice que un cuerpo se encuentra en equilibrio estático respecto de un sistema de referencia cuando su centro de masas, o centro de gravedad, se encuentra en reposo respecto de él.
Se dice que un cuerpo se encuentra en equilibrio cinético respecto de un sistema de referencia cuando su centro de masas, o centro de gravedad, se encuentra trasladándose con velocidad lineal constante (M.R.U.) y al mismo tiempo se encuentra rotando con una velocidad angular constante (M.C.U.) respecto de él. Si sólo se cumple la primera condición se dice que el cuerpo se encuentra en equilibrio traslacional y si sólo se cumple la segunda se dice que se encuentra en equilibrio rotacional.
FUERZAS
La noción de fuerza surgió al apreciar la tensión muscular (jalar o empujar un cuerpo).
Para elevar una piedra, desplazar un cuerpo, tensar una cuerda, etc. se necesita cierta tensión de los músculos, diferente en cada caso.
La fuerza es una magnitud vectorial que es una medida del grado de interacción, o acción mutua, que existe entre los cuerpos o entre sus partículas.
Ésta es la causa que origina que los cuerpos alteren, o tiendan a alterar, su estado de movimiento.
También es la causa que origina la deformación de los cuerpos reales. Por ejemplo, cuando una persona patea una lata, puede adquirir movimiento y también deformarse.
Según la ley de Hooke, la fuerza F necesaria para deformar linealmente un cuerpo deformable (resorte) es directamente proporcional a su elongación x (longitud deformada).
Matemáticamente: F = k.x
La naturaleza de las fuerzas que actúan sobre los cuerpos, que no son de escala microscópica, son de origen gravitatorio o electromagnético.
A continuación veamos algunos ejemplos.
Consideremos una persona que empuja una caja que se encuentra sobre una superficie áspera.
La naturaleza de la interacción entre la persona y la caja es de origen electromagnético (entras las moléculas de la mano de la persona y las de la caja se genera una repulsión eléctrica). La naturaleza de la interacción entre la caja y la superficie también es de origen electromagnético, en este caso, de atracción eléctrica.
Como segundo ejemplo consideremos un imán que ejerce una acción a distancia sobre unos clavos. La naturaleza de la interacción entre el imán y los clavos también es de origen electromagnético (entre las partículas de magnetita del imán y las de los clavos se genera una atracción magnética).
Usualmente las fuerzas se suman con el objetivo de reemplazarlas por una sola denominada fuerza resultante.
Al sumar dos fuerzas que tienen la misma dirección, el módulo de la fuerza resultante se obtiene sumando aritméticamente los módulos de cada una de ellas.
Al sumar dos fuerzas que tienen dirección opuesta, el módulo de la fuerza resultante se obtiene restando aritméticamente los módulos de cada una de ellas.