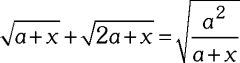ÁLGEBRA CAYETANO HEREDIA EXAMEN INGRESO UNIVERSIDAD UPCH RESUELTO PDF
PREGUNTA 1 :
PREGUNTA 2 :
Reduzca
322/5+(−27)1/3+163/4
A) 8
B) 9
C) 11
D) 7
E) 10
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 3 :
Simplifique
(√7+√5)2+(√7–√5)2
A) 2√7
B) 2√5
C) 7+√5
D) 24
E) 4
RESOLUCIÓN :
Desarrollando los binomios o en todo caso aplicando directamente legendre , se tiene lo siguiente :2√72+2√52=2(7+5)=24
Rpta. : "D"
PREGUNTA 4 :
Sabiendo que
a+b=5
ab=1
Halle a3+b3
A) 120
B) 110
C) 122
D) 115
E) 90
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 5 :
Siendo x∈ℤ, resuelva
A) {–1/2}
B) –1/12
C) {1/12}
D) 1/12
E) Ø
RESOLUCIÓN :
Se observa que x=–1/12 no pertenece a los enteros, razón por la cual la ecuación no tiene solución en los enteros (CS=∅).
Rpta. : "E"
PREGUNTA 7 :
Sabiendo que:
P(x+3)=2x+1
P(Q(x))=2x+3
Calcula: Q(P(1))
a) 4
b) 3
c) 1
d) 2
e) 5
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 8 :
Halle el resto en la división
A) – 1
B) – 2
C) – 3
D) 4
E) – 4
RESOLUCIÓN :
I) Por teorema del resto x=–1
II) R=2(–1)20+(–1)15+6(–1)7– (–1)2+4
=2 – 1– 6 – 1+4 =–2
Rpta. : "B"
PREGUNTA 9 :
Halle la mayor solución en
x2+3x–1=0
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 10 :
Si –5<x<–2
Halle el intervalo de variación de 5–x2
A) 〈–19;1〉
B) 〈–15;1〉
C) 〈1;19〉
D) 〈0;5〉
E) 〈2;8〉
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 11 :
Si a y b son las raíces de
x2–4x+4=0
Calcule a2+b2
A) 5
B) 7
C) 6
D) 8
E) 9
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 13 :
En el siguiente esquema de Ruffini:
Calcula a+b+c+d+e
A) 4
B) 3
C) 1
D) –1
E) 0
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 14 :
Halla el número de factores primos de
a4b – 9a2b3– 2a3b2+18ab4
siendo a y b números primos.
A) 11
B) 9
C) 4
D) 5
E) 3
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 15 :
Simplifique
A) x – 1
B) 2
C) 1
D) x
E) 5
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 16 :
Una empresa aceitera ha envasado 3000 litros de aceite en 1200 botellas de dos y de cinco litros. El número de botellas de cinco litros que se han utilizado es:
A) 200
B) 240
C) 300
D) 360
E) 420
RESOLUCIÓN :
Sea:
X: cantidad de botellas de 2 litros
Y: cantidad de botellas de 5 litros
De acuerdo a los datos tenemos:
Por lo tanto, se han utilizado 200 botellas de 5 litros.
Rpta. : "A"
PREGUNTA 17 :
Juan fabrica armarios de oficina y planea venderlos a S/350 la unidad. Él estima que la fabricación le genera costos indirectos fijos que ascienden a S/11200, a lo que hay que sumarle costos de producción de S/200 por unidad fabricada. ¿Cuántas unidades debe vender Juan para obtener una ganancia de S/4550?
A) 115
B) 105
C) 135
D) 125
E) 100
RESOLUCIÓN :
Precio venta = S/350 (c/u)
Costos fijos = S/11200
Costo de producción = S/ 200 (c/u)
Ganancia = S/ 4550
Número de armarios de oficina=x
Luego:
350.x =200.x+11200+4550
⇒ 150.x=15750
⇒ x =105
Entonces el número de unidades que se deben vender será: 105 armarios de oficina
Rpta. : "B"
PREGUNTA 18 :
Qué valor de x verifica la igualdad
A) 3a/2
B) −3a/2
C) 2a/3
D) −2a/3
E) −a/2
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 19 :
Hallar el valor de (m+1)2, si la ecuación mx2–4x+4(2–m)=0 tiene solución única.
A) 1
B) 4
C) 9
D) 0
E) 16
RESOLUCIÓN :
Se tiene mx2–4x+4(2–m)=0
Como tiene solución única
∴ (m+1)2=(1+1)2=4
Rpta. : "B"
PREGUNTA 20 :
Hallar el equivalente de
A) √5−1
B) √2+1
C) √5+√2
D) √5+1
E) √2−1
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 21 :
En un rectángulo su base mide “x” y su perímetro mide “2a”, entonces el valor que debe tomar su base es
A) –1<x<a
B) –1<x <a/2
C) a<x<2a
D) 0<x<a
E) a< x<0
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 22 :
La empresa TANOYE fabrica accesorios para iluminación. El costo de fabricación C y el número de unidades x se relacionan por la expresión:
¿Cuántos accesorios se deben producir para minimizar el costo?
A) 25
B) 30
C) 35
D) 40
E) 20
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 23 :
En el gráfico de las funciones logarítmicas:
Determina el valor de a+b.
A) 2+log2
B) 4+log4
C) 2+2log2
D) 4+log2
E) 4+2log3
RESOLUCIÓN :
Para determinar (a;b) según el gráfico, debemos igualar
f(x) =g(x)
log(x+2) = log(6–x)
→ x+2=6–x
⇒ 2x=4
⇒ x=2
Reemplazando
y=f(2)=g(2)
y=log4=log22=2log2
El punto en común es (2;2log2 )
∴ a+b=2+2log2
Rpta. : "C"


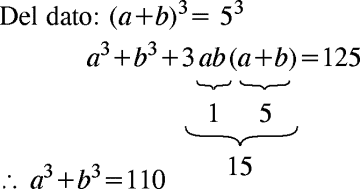




.png)