GEOMETRÍA UNHEVAL EXAMEN INGRESO UNIVERSIDAD VALDIZAN RESUELTO PDF
CONTENIDO TEMÁTICO DEL EXAMEN UNHEVAL DEL CURSO DE GEOMETRÍA
1. TRIÁNGULOS. PROPIEDADES BÁSICAS:
Definición .
Teoremas fundamentales
Clasificación de los triángulos.
2. LÍNEAS NOTABLES:
Bisectriz Interior.
Bisectriz Exterior.
Altura.
Mediana.
Mediatriz.
Teoremas.
Angulo determinado por las bisectrices de un ángulo interior y un ángulo exterior.
Ángulo determinado por las bisectrices de dos ángulos interiores.
Ángulo determinado por las bisectrices de dos ángulos exteriores
Triángulos rectángulos notables de 45°, 30° y 60°, 37° y 53°, 16° y 74°, 15° y 75°, 37°/2, 53°/2.
3. CONGRUENCIA DE TRIÁNGULOS:
Caso: (ALA). Ángulo - Lado - Ángulo.
Caso: (LAL). Lado - Ángulo - Lado.
Caso: (LLL). Lado - Lado - Lado.
Teorema de los puntos medios.
Propiedad de la Bisectriz.
Propiedad de la mediatriz.
Propiedad de la Mediana relativa a la hipotenusa.
4. POLÍGONOS:
Definición.
Clasificación.
De acuerdo a su región.
Polígonos convexos y no convexos.
De acuerdo a su número de lados: triángulo, cuadrilátero, pentágono, etc., de acuerdo a sus ángulos y a sus lados:
Polígono equilátero
Polígono equiángulo
Polígono regular:
Propiedades
número total de diagonales en un Polígono
Suma de ángulos internos en un polígono convexo
Medida de un Ángulo interno de polígonos equiángulos y regulares
Suma de ángulos externos en un polígono convexo
Número total de diagonales medias en un polígono.
5. CUADRILÁTEROS:
Definición.
Clasificación de los cuadriláteros convexos.
Trapecios:
Trapecio isósceles
Trapecio escaleno
Trapecio rectángulo.
Propiedades en el trapecio:
la mediana de un trapecio
el segmento que une los puntos medios de las diagonales de un trapecio
Paralelogramos: rombo, romboide, rectángulo, cuadrado.
6. CIRCUNFERENCIA I :
propiedades fundamentales en la circunferencia.
Ángulos en la circunferencia:
ángulo central
ángulo inscrito
ángulo semi - inscrito
ángulo interior
ángulo exterior.
7 . CIRCUNFERENCIA II :
cuadriláteros inscriptibles y circunscriptibles.
Teorema de Poncelet.
Teorema de Pitot.
8. PUNTOS NOTABLES:
Incentro:
Teoremas de Poncelet
Pitot y Steiner.
Excentro: propiedades.
Ortocentro:
Ortocentro para triángulos acutángulos, rectángulos y obtusángulos.
Baricentro : propiedades .
Circuncentro :
Circuncentro para triángulos acutángulos, rectángulos y obtusángulos.
9 . PROPORCIONALIDAD :
Definición y propiedades.
Teorema de Thales.
Teorema de la Bisectriz.
Teorema del incentro.
Teorema del excentro.
Teorema de Menelao.
10. SEMEJANZA DE TRIÁNGULOS:
Definición y propiedades.
Casos de semejanza.
11. PRISMA:
Definición y propiedades
Clasificación de un prisma recto.
Área lateral, total y volumen de un prisma recto.
12. CILINDRO RECTO:
Definición y propiedades.
Cilindro de revolución.
Área lateral, total y volumen de un cilindro de revolución.
13. PIRÁMIDE:
Definición y propiedades.
Clasificación.
Área lateral, total y volumen de una pirámide.
14. CONO RECTO:
Definición y propiedades.
Clasificación.
Área lateral, total y volumen de un cono de revolución.
15. ESFERA:
Definición y propiedades.
Área de la superficie esférica.
Volumen de la esfera
PREGUNTA 1:
En una recta se ubican los puntos consecutivos: L, O, P, E y Z.
Tal que LO=2(OP) y EZ = 3(PE).
Si EZ+LP=36 cm, halle OE.
A) 15 cm
B) 12 cm
C) 10 cm
D) 9 cm
E) 16 cm
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 2:
Calcule la medida del ángulo “x” del siguiente gráfico, siendo L1//L2
A) 15º
B) 30º
C) 45º
D) 60º
E) 75º
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 3:
Si el ángulo externo de un polígono regular mide 36º, calcule el mayor número de diagonales que se puede trazar:
A) 20
B) 28
C) 35
D) 44
E) 54
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 4:
En la figura, calcule el valor de “X”:
A) 59º
B) 60º
C) 45º
D) 36º
E) 10º
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 5:
Las diagonales de un rombo miden 12 y 16 cm. Halle la distancia que hay entre dos lados opuestos:
A) 9,4 cm
B) 9,8 cm
C) 9,7 cm
D) 9,6 cm
E) 9,5 cm
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 6:
Halle el área del triángulo rectángulo cuya hipotenusa se encuentra dividida en 5 y 12 cm y mantiene una circunferencia inscrita de radio “r”
A) 40 cm²
B) 50 cm²
C) 60 cm²
D) 70 cm²
E) 80 cm²
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 7 :
En la figura adjunta: si la medida del segmento AB es 8 cm y la medida del radio OM es 5 cm, entonces el área del rectángulo ABCD es
A) 40 cm²
B) 48 cm²
C) 56 cm²
D) 64 cm²
E) 72 cm²
RESOLUCIÓN :
Rpta. : "B"
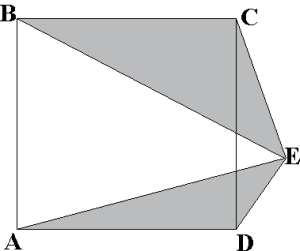
PREGUNTA 8:
La figura ABCD es un cuadrado de lado 5m. Calcule el área de la región sombreada.
A) 12,5 m²
B) 9,5 m²
C) 15,5 m²
D) 8,5 m²
E) 5,5 m²
RESOLUCIÓN :
pta. : "A"
PREGUNTA 9:
En la figura mostrada, halle el área de la región sombreada, si “O” es el centro:
A) 30𝜋 cm²
B) 25𝜋 cm²
C) 15𝜋 cm²
D) 40𝜋 cm²
E) 24𝜋 cm²
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 10:
Los catetos del triángulo rectángulo DBE miden “a” y “b”. si AD = DE = EC. Halle el área del triángulo ABC.
A) 3 𝑎. 𝑏
B) 2 𝑎. 𝑏
C) 1,5𝑎. 𝑏
D) 2/3 𝑎. 𝑏
E) 𝑎. 𝑏
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 11:
En la figura mostrada, el área de la región triangular ABC es 42 m². Si PC=2BP y AQ=2QC, halle el área de la región mostrada.
A) 2m²
B) 4m²
C) 3m²
D) 2,5m²
E) 3,5m²
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 12:
En el gráfico, calcule “x”
A) 5
B) 4
C) 3
D) 2
E) 1
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 13:
En el gráfico, AB =6m y BC =8m; D y E son puntos de tangencia. Halle el área de la región sombreada
A) 10m²
B) 16m²
C) 8m²
D) 6m²
E) 12m²
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 14:
Un acuarista elaboró un novedosos acuario, cuya base es un hexágono de 10 cm de arista, y una altura de 15 cm. Halle la cantidad de vidrio que utilizó:
A) (900 + 150√3) cm²
B) 800 cm²
C) 1800 cm²
D) 1000 cm²
E) 700√3 cm²
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 15:
En la figura dada, halle la ecuación de la recta L2 que pasa por el punto A(2;6) y es perpendicular a la recta L1.
A) 4x + 3y= 26
B) 3x + 4y = 26
C) 4x − 3y = 23
D) 3x − 4y = 23
E) 5x − y = 26
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 16 :
¿ Cuál es la ecuación de la recta que pasa por el origen y es perpendicular a la recta
3x–2y = 6 ?
A) 2x + 3y = 0
B) 3x + 2y = 1
C) 2x – 3y = 6
D) 3x + 4y = 2
E) 2x – 3y = 4
RESOLUCIÓN :
Rpta. : "A"
