MOVIMIENTO CIRCULAR UNIFORME EJERCICIOS RESUELTOS DE MCU – INGRESO UNIVERSIDAD
EJERCICIO 1
Un disco gira con una rapidez angular constante de 8prad/s, determine el número de revoluciones en 12 minutos.
A) 48
B) 36
C) 576
D) 816
E) 2880
EJERCICIO 2
Una partícula de 120 vueltas en 0,5min. ¿Qué frecuencia posee?
A) 1Hz
B) 2Hz
C) 6Hz
D) 8Hz
E) 4Hz
EJERCICIO 3
Una partícula de 5 vueltas en 0,2s. ¿Qué frecuencia posee (en Hz)?
A) 25
B) 10
C) 20
D) 8
E) 15
EJERCICIO 4
Una partícula gira con movimiento circular uniforme y con velocidad angular de 8𝛑rad/s. Para dar 80 vueltas se requiere:
A) 10s
B) 40s
C) 24s
D) 15s
E) 20s
EJERCICIO 5
Determine su frecuencia de rotación (en r.p.s.) de un cuerpo con M.C.U. y rapidez de 5prad/s.
A) 5/2
B) 3/4
C) 1
D) 2/3
E) 3/2
EJERCICIO 6
Determine la rapidez angular (en rad/s) de la manecilla del minutero de un reloj.
A) 𝛑/1800
B) 𝛑/3600
C) 𝛑/60
D) 𝛑/30
E) 𝛑/1200
EJERCICIO 7
Determine la rapidez angular (en rad/s) de la manecilla del horario de un reloj.
A) 𝛑/21600
B) 𝛑/7200
C) 𝛑/80
D) 𝛑/90
E) 𝛑/1800
EJERCICIO 8
De dos puntos diametralmente opuestos parten dos coches al encuentro con rapideces de 𝛑/5 y 𝛑/20 rad/s. Luego de qué tiempo se encuentran.
A) 4s
B) 6s
C) 2s
D) 5s
E) 8s
EJERCICIO 9
En una pista circular, un ciclista puede dar tres vueltas en un minuto y otro solo dos vueltas en un minuto. Si ambos pasan por dos puntos diametralmente opuestos simultáneamente y avanzan uno al encuentro del otro, determine en qué tiempo se encontrarían.
A) 2s
B) 6s
C) 4s
D) 5s
E) 8s
EJERCICIO 10
En un velódromo circular, dos ciclistas salen de puntos diametralmente opuestos con rapidez constante y uno a la persecución del otro. Si uno de los ciclistas da 6 vueltas por minuto y el otro 5 vueltas por minuto, ¿cuánto tiempo, después de la salida, el segundo alcanza al primero?
A) 10s
B) 32s
C) 25s
D) 15s
E) 30s
EJERCICIO 11
Una mosca está ubicada en un disco de 45RPM a proximidades del centro del disco. Determinar la rapidez angular de la mosca (en rad/s).
A) 3𝛑/4
B) 3𝛑/2
C) 3𝛑/8
D) 7𝛑/6
E) 8𝛑/3
EJERCICIO 12
Un disco cuyo radio es 10cm gira a razón de 75RPM. Determine la rapidez tangencial (en cm/s) de los puntos que se encuentran a 2cm del borde.
A) 4𝛑
B) 5𝛑
C) 10𝛑
D) 20𝛑
E) 0
EJERCICIO 13
Una partícula con movimiento circular uniforme gira alrededor de un punto fijo con una rapidez de 4𝛑 m/s, la distancia del punto a la trayectoria de la partícula es de 5cm. ¿Cuál será su rapidez en rad/s?
A) 20𝛑
B) 30𝛑
C) 50𝛑
D) 40𝛑
E) 80𝛑
EJERCICIO 14
Un insecto recorre el borde de una tapa circular con una rapidez de 0,25cm/s. ¿Qué longitud bordeara al cabo de 4s?
A) 2cm
B) 1cm
C) 2,5cm
D) 4cm
E) 8cm
EJERCICIO 15
Las hélices de una licuadora giran a razón de 300rad/s. Si realizan MCU determine la rapidez tangencial en m/s de un punto que esta a 5cm del eje de giro.
A) 18
B) 36
C) 24
D) 16
E) 15
EJERCICIO 16
Un punto gira sobre una circunferencia de 10cm de radio con una velocidad angular de 0,3rad/s. Determine su rapidez tangencial (en cm/s).
A) 4𝛑
B) 5𝛑
C) 6𝛑
D) 3𝛑
E) 8𝛑
EJERCICIO 17
La rueda de la fortuna es una de las mayores atracciones de una feria. Consiste de una rueda gigante en posición vertical con asientos unidos al borde y que gira alrededor de un eje horizontal perpendicular al plano de la rueda. Considere una rueda de 30m de diámetro que gira de manera uniforme empleando 20 segundos cada vuelta. Determine la rapidez lineal (en m/s) de un pasajero si este está ubicado al borde la rueda.
A) 7,5
B) 4,7
C) 2,3
D) 6,8
E) 3,2
EJERCICIO 18
Un muchacho parte del eje de giro de un disco que gira con 0,2rad/s en dirección de uno de sus radios con una rapidez de 15cm/s respecto al centro del disco. Determine su rapidez cuando se encuentra a 1m del eje (en cm/s).
A) 24
B) 15
C) 22
D) 23
E) 25
EJERCICIO 19
Un cuerpo se mueve en una trayectoria circular con rapidez constante. Si luego duplica su rapidez mientras viaja a lo largo de la misma trayectoria, su período cambia en un factor de:
A) 1/2
B) 1/4
C) 3/5
D) 2/3
E) 3/2
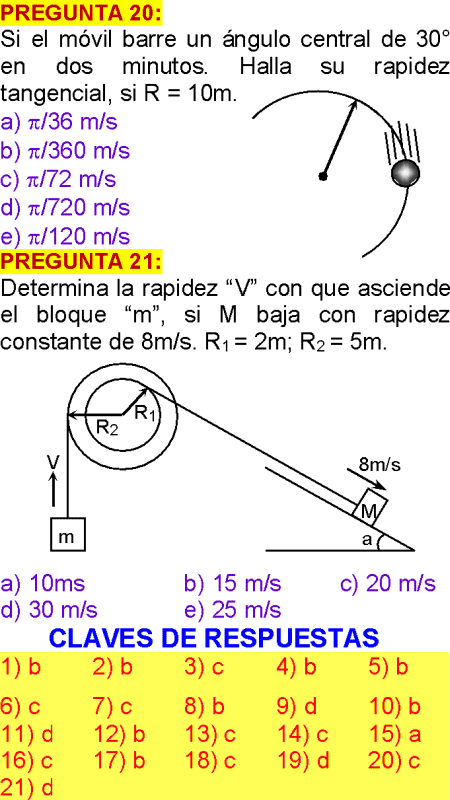
EJERCICIO 20
La hélice de un helicóptero se mueve de acuerdo a la ecuación θ = 20t, donde q se mide en radianes y t en segundos. Determina el número de vueltas que da la hélice en 1,6𝛑s.
A) 16
B) 24
C) 12
D) 4
E) 8
EJERCICIO 21
La velocidad angular de un disco de 3m de radio es de 24rad/s. Calcule el módulo de la velocidad tangencial (en m/s) de un punto del disco ubicado a 1m de su periferia en la dirección radial.
A) 48
B) 27
C) 24
D) 36
E) 45
EJERCICIO 22
La lavadora es un aparato electrodoméstico, cuyo uso se ha vuelto común en las familias para lavado de ropas. Ella cuenta con un tambor central grande de radio r=20cm que puede rotar debido a un motor eléctrico. Si el tambor rota con frecuencia de 20Hz en el centrifugado, determine la rapidez lineal de un punto del tambor (en m/s).
A) 4𝛑
B) 5𝛑
C) 6𝛑
D) 3𝛑
E) 8𝛑
EJERCICIO 23
Una partícula se mueve con MCU. Si la magnitud de la aceleración centrípeta es de 90m/s2 y el radio es de 10m. Halle la frecuencia de la partícula en Hertz.
A) 1,5𝛑 – 1
B) 4/𝛑
C) 2/𝛑
D) 1/𝛑
E) 3/𝛑
EJERCICIO 24
Un piloto de avión bien entrenado soporta durante tiempos breves, aceleraciones de hasta 8m/s2 veces la de la gravedad, sin perder el movimiento. Para un avión que vuela a 1800km/h, el radio de giro mínimo que produzca una aceleración que el piloto puede soportar es (en m): ... (g = 10m/s2)
A) 3125
B) 5275
C) 3805
D) 4225
E) 7525
EJERCICIO 25
En los juegos de azar un objeto de 0,5kg gira uniformemente en un círculo sobre una superficie horizontal sin fricción. El objeto se encuentra unido por una cuerda de 14cm al eje de giro. Si el objeto completa 3 revoluciones por segundo, la aceleración radial es:
A) 47,8
B) 44,5
C) 49,7
D) 47,5
E) 41,5
EJERCICIO 26
El disco de vinilo fue un medio de almacenamiento de sonido analógico muy usado en la década de los 80. Tenía un diámetro de 30cm y frecuencia 33 RPM. Este disco ha sido ya superado por los digitales, como el disco compacto de menor tamaño y mayor almacenamiento. Respecto al disco de vinilo, determine la rapidez tangencial, en cm/s, de un punto ubicado a 5cm del borde del disco.
A) 10𝛑
B) 11𝛑
C) 12𝛑
D) 13𝛑
E) 16𝛑
EJERCICIO 26
Un cilindro vacío de radio en su base 0,4m gira con una velocidad angular constante a 150r.p.s. respecto a su eje vertical. Se dispara un proyectil horizontalmente, de modo que pasa por el eje de rotación. Determine la máxima rapidez (en m/s) del proyectil (constante) para que atraviese al cilindro haciendo un solo agujero.
A) 120
B) 150
C) 180
D) 240
E) 160
EJERCICIO 27
Los satélites artificiales son objetos de fabricación humana que se han colocado en órbita alrededor de la Tierra y, dependiendo de su uso, tienen diferentes periodos orbitales. Por ejemplo, si para las empresas celulares con tecnología GPS el periodo orbital es de 14 horas, ¿cuál es la magnitud de velocidad lineal con la que gira el satélite (en m/s)? (RTierra= 6×106m).
A) 120
B) 150
C) 180
D) 100
E) 160
EJERCICIO 28
Un satélite terrestre realiza un MCU. El satélite gira alrededor de la Tierra a 644 km de la superficie terrestre. El tiempo que tarda en dar una vuelta (periodo) es de 98 minutos. Calcule aproximadamente la aceleración del satélite en m/s2. (RTierra= 6378 km)
A) 11
B) 10
C) 9
D) 7
E) 8
EJERCICIO 29
Respecto al movimiento circular uniforme (MCU), determine si las siguientes proposiciones son verdaderas (V) o falsas (F) y marque la alternativa correspondiente.
I. En el MCU no existe aceleración
II. En el MCU la velocidad lineal es constante
III. En el MCU la aceleración es constante
A) FFF
B) FVF
C) VFF
D) FFV
E) VVV
EJERCICIO 30
Respecto a las cantidades cinemáticas angulares, determine si las siguientes proposiciones son verdaderas (V) o falsas (F) y marque la alternativa correspondiente.
I. El desplazamiento angular es una cantidad vectorial.
II. La velocidad angular es perpendicular al plano de giro y su sentido se determina con la regla de la mano derecha.
III. La aceleración angular es siempre paralela a la velocidad angular.
A) VVV
B) VFV
C) VFF
D) FFV
E) FVF
EJERCICIO 31
Respecto de las cantidades cinemáticas angulares, determine si cada una de las siguientes proposiciones es verdadera (V) o falsa (F) y marque la secuencia correcta:
I. La velocidad angular tiene la misma orientación que el desplazamiento de la partícula.
II. La velocidad angular es un vector perpendicular al plano de rotación.
III. La aceleración angular es perpendicular a la velocidad angular.
A) VVV
B) VVF
C) FVV
D) FVF
E) FFV
EJERCICIO 32
Respecto a una partícula en movimiento circular, determine si cada una de las siguientes proposiciones es verdadera (V) o falsa (F) y marque la secuencia correcta:
I. La velocidad de la partícula es perpendicular a su posición.
II. La velocidad angular es perpendicular a la velocidad.
III. La aceleración angular y la velocidad angular siempre tienen la misma orientación.
A) VVF
B) VFF
C) FVF
D) VFV
E) VVV
PRACTICA BÁSICA
EJERCICIO 1 :
Una partícula con MCU tarda 12s en realizar tres vueltas, ¿qué tiempo tardará en realizar sólo una vuelta?
a) 10 s
b) 6
c) 5
d) 4
e) 9
EJERCICIO 2 :
Una partícula con MCU tarda 8s en realizar cuatro vueltas, ¿qué tiempo tardará en realizar sólo una vuelta?
a) 8 s
b) 2
c) 6
d) 4
e) 10
EJERCICIO 3 :
Una partícula con MCU realiza cinco vueltas en 45s, ¿cuál será su período?
a) 10 s
b) 16
c) 3
d) 9
e) 8
EJERCICIO 4 :
Una partícula con MCU realiza seis vueltas en 18s, ¿cuál será su período?
a) 6 s
b) 12
c) 3
d) 5
e) 9
EJERCICIO 5 :
Una partícula con MCU realiza 12 vueltas en 3s, ¿cuál será su frecuencia?
a) 10 RPS
b) 6
c) 5
d) 4
e) 9
EJERCICIO 6 :
Una partícula con MCU realiza 10 vueltas en 5s, ¿cuál será su frecuencia?
a) 5RPS
b) 1
c) 10
d) 6
e) 2
EJERCICIO 7 :
Una partícula con MCU tiene un período de 12s, ¿qué tiempo tardará en realizar media vuelta?
a) 8s
b) 2
c) 6
d) 4
EJERCICIO 8 :
Una partícula con MCU tiene una frecuencia de 5RPS, ¿qué tiempo tardará en realizar 30 vueltas?
a) 5s
b) 3
c) 20
d) 10
e) 6
EJERCICIO 9 :
Una partícula con MCU tarda 4s en realizar una vuelta, ¿qué tiempo tardará en realizar tres vueltas?
a) 8 s
b) 12
c) 6
d) 16
e) 10
e) 10
EJERCICIO 10 :
Una partícula con MCU tiene una frecuencia de 8RPS, ¿cuántas vueltas realizará en 15s?
a) 75 s
b) 30
c) 20
d) 90
e) 120
EJERCICIO 11 :
Se sabe que una partícula dio 16 vueltas en 8 segundos.
¿Qué ángulo giraría dicha partícula en 10 segundos?
a) 10𝛑rad
b) 20𝛑
c) 30𝛑
d) 40𝛑
e) 50𝛑
EJERCICIO 12 :
¿Qué ángulo giraría una hélice en 2 minutos si su velocidad angular es 3rad/s?
a) 300 rad
b) 320
c) 340
d) 360
e) 400
EJERCICIO 13 :
El aspa de un ventilador giró 360 vueltas en un minuto. ¿Qué ángulo giraría dicha aspa en 5 segundos?
a) 60𝛑rad
b) 40𝛑
c) 50𝛑
d) 180𝛑
e) 360𝛑
EJERCICIO 14 :
¿Cuál será la velocidad angular de la Tierra en rad/h al girar alrededor de su eje de rotación?.
a) 𝛑/6
b) 𝛑/12
c) 3𝛑/5
d) 𝛑/24
e) 𝛑/8
PREGUNTA 1 :
Dos móviles A y B parten de dos puntos diametralmente opuestos de una pista circular, desplazándose en sentido horario con velocidades angulares de 𝛑/2 y 𝛑/3 rad/s, respectivamente. El tiempo, en segundos, en que se encuentran es
A) 2
B) 1
C) 8
D) 4
E) 6
RESOLUCIÓN :
Rpta. : "E"
PRIMERA PRACTICA
PREGUNTA 1 :
Señala verdadero (V) o falso (F) según corresponda:
I) En el M.C.U. no existe aceleración.
II) En el M.C.U. la rapidez tangencial siempre es constante a un mismo nivel.
III) En el M.C.U. la rapidez tangencial es perpendicular a la rapidez angular.
a) VVV
b) FVV
c) FFF
d) VFV
e) FVF
Rpta. : "B"
PREGUNTA 2 :
Una partícula se mueve con M.C.U.; alrededor de una circunferencia de 2m de radio. Calcula la rapidez tangencial sabiendo que la partícula da 8 vueltas en 16s.
a) 𝛑m/s
b) 2𝛑m/s
c) 3𝛑m/s
d) 2m/s
e) 3m/s
Rpta. : "B"
PREGUNTA 3 :
Una partícula con M.C.U barre un ángulo de 81 𝛑rad en 9s. Si el radio es (6/𝛑)m ¿Cuál es su rapidez tangencial?
a) 12 m/s
b) 36 m/s
c) 54 m/s
d) 108 m/s
e) 72 m/s
Rpta. : "C"
PREGUNTA 4 :
Una partícula describe un arco de 40m con un M.C.U en 10s. Calcula su rapidez angular si el radio es de 10m.
a) 0,2 rad/s
b) 0,4 rad/s
c) 0,35 rad/s
d) 0,8 rad/s
e) 0,25 rad/s
Rpta. : "B"
PREGUNTA 5 :
Un cuerpo con MCU realizó 20 vueltas en 4 segundos. Halla su rapidez angular en rad/s.
a) 20𝛑
b) 10𝛑
c) 5𝛑
d) 16𝛑
e) 8𝛑
Rpta. : "B"
PREGUNTA 6 :
Una piedra de amolar rota con una rapidez angular constante. Un punto ubicado a 2cm de la periferia medidos en la dirección radial, posee una rapidez tangencial 1/5 menor que la que posee un punto ubicado en la periferia. ¿Cuál es el radio de la piedra?
a) 25cm
b) 55cm
c) 10cm
d) 12cm
e) 14cm
Rpta. : "C"
PREGUNTA 7 :
Un cuerpo realiza un M.C.U con un período de 11s. Si su rapidez tangencial es 4m/s, halla el radio de la circunferencia (𝛑 = 22/7)
a) 1m
b) 2
c) 3,5
d) 7
e) 11
Rpta. : "D"
PREGUNTA 8 :
Una partícula con M.C.U. posee una rapidez de 30m/s. Si el radio de la circunferencia que se describe es de 0,5m., halla su frecuencia de rotación en R.P.M.
a) 900/𝛑
b) 1800/𝛑
c) 200/𝛑
d) 360/𝛑
e) 3000/𝛑
Rpta. : "B"
PREGUNTA 9 :
Una estrella fugaz brilla en el cielo durante 3,14s., describiendo en ese tiempo un arco de 9°. ¿Cuál fue su rapidez en km/s si su distancia al observador es 80km.?
a) 1
b) 2
c) 3
d) 4
e) 5
Rpta. : "D"
PREGUNTA 10 :
Una partícula describe una circunferencia de 2m de radio, si la aceleración centrípeta es 8m/s². ¿Cuál es su frecuencia en R.P.M.?
a) 30/𝛑
b) 60/𝛑
c) 50/𝛑
d) 75/𝛑
e) 90/𝛑
Rpta. : "B"
PREGUNTA 11 :
Una partícula gira con M.C.U., de modo que su rapidez tangencial es 2,5 m/s y su rapidez angular es 14 rad/s. ¿Cuánto vale su aceleración centrípeta?
a) 25m/s²
b) 30 m/s²
c) 35 m/s²
d) 40 m/s²
e) 45 m/s²
Rpta. : "C"
PREGUNTA 12 :
En una pista circular se cruzan dos partículas con rapidez angular constante de 2 y 3rad/s. Halla el tiempo adicional suficiente para que los vectores rapidez tangencial de estas partículas formen un ángulo de 60°.
a) 0,2s
b) 0,4
c) 0,6
d) 0,8
e) 0,9
Rpta. : "D"
PREGUNTA 13 :
Un cubo de agua atado al final de una cuerda de 50 cm es girado en un plano vertical, entonces indique el valor de la velocidad lineal que debe adquirir para que la aceleración centrípeta sea igual a la aceleración de la gravedad.
( g=9,8 m/s²; √10≈3,2)
A) 2,24 m/s
B) 3,5 m/s
C) 2,1 m/s
D) 1,9 m/s
E) 1,2 m/s
Rpta. : "A"
PREGUNTA 14 :
Una esfera realiza MCU a razón de 15 RPM con una radio de 2 m. Respecto a ello, indique la secuencia correcta de verdad (V) o falsedad (F).
I. El periodo es de 2 s.
II. La rapidez angular es de 0,5𝛑 rad/s.
III. La rapidez lineal es de 𝛑 m/s.
A) FFV
B) FVV
C) FVF
D) VVF
D) VVV
Rpta. : "B"
PREGUNTA 15 :
En un velódromo circular, dos ciclistas salen de puntos diametralmente opuestos con rapidez constante y uno a la persecución del otro. Si uno de los ciclistas da 6 vueltas por minuto y el otro 5 vueltas por minuto, ¿cuánto tiempo, después de la salida, el segundo alcanza al primero?
A) 20 s
B) 22 s
C) 25 s
D) 40 s
D) 30 s
Rpta. : "E"
PREGUNTA 16 :
La lavadora es un aparato electrodoméstico, cuyo uso se ha vuelto común en las familias para lavado de ropas. Ella cuenta con un tambor central grande de radio r que puede rotar debido a un motor eléctrico. Si el tambor rota con frecuencia de 20 Hz en el centrifugado, determine la rapidez lineal de un punto del tambor.
(r =20 cm).
A) 8𝛑 m/s
B) 5𝛑 m/s
C) 6𝛑 m/s
D) 4𝛑 m/s
E) 4𝛑 m/s
Rpta. : "A"
PREGUNTA 17 :
Pera SAT-1 así se llama el primer satélite oficial del Perú, puesto en órbita el 15 de setiembre de 2016 con una duración de 10 años. Tiene una cobertura de todo el territorio peruano y de esta manera aporta en seguridad y defensa nacional, previsión de desastres entre otros. Su masa está alrededor de los 400 kg y órbita a 694 km de la Tierra dando 15 vueltas diarias a su alrededor. Con esta información determine la rapidez lineal del satélite.
(RTierra =6400 km)
A) 25420 km/h
B) 26450 km/h
C) 27858 km/h
D) 29475 km/h
E) 20445 km/h
Rpta. : "C"
PREGUNTA 18 :
La rueda de la fortuna es una de las mayores atracciones de una feria. Consiste de una rueda gigante en posición vertical con asientos unidos al borde y que gira alrededor de un eje horizontal perpendicular al plano de la rueda. Considere una rueda de 30 m de diámetro que gira de manera uniforme empleando 20 segundos cada vuelta. Determine la rapidez lineal de un pasajero si este está ubicado al borde la rueda.
A) 2,8 m/s
B) 3,5 m/s
C) 4,7 m/s
D) 5,6 m/s
E) 4,6 m/s
Rpta. : "C"
PREGUNTA 19 :
El disco de la muerte es un disco giratorio de 6 m de radio donde los niños se divierten caminando sobre el, que gira con 5 s de periodo. Determine la rapidez lineal en un niño que está a 1 m de la periferia.
A) 4,4 m/s
B) 5,36 m/s
C) 6,28 m/s
D) 7,8 m/s
D) 7,2 m/s
Rpta. : "C"
PREGUNTA 20 :
Los satélites artificiales son objetos de fabricación humana que se han colocado en órbita alrededor de la Tierra y, dependiendo de su uso, tienen diferentes periodos orbitales. Por ejemplo, si para las empresas celulares con tecnología GPS el periodo orbital es de 14 horas, ¿cuál es la magnitud de velocidad lineal con la que gira el satélite?
(RTierra =6×10⁶ m).
A) 755 m/s
B) 723 m/s
C) 736 m/s
D) 738 m/s
E) 747 m/s
Rpta. : "D"
PREGUNTA 21 :
Cuando un auto da una curva circular en una pista, existe un efecto a volcar en el auto, y este efecto aumenta si también aumenta la rapidez tangencial con que se da la curva. Si la máxima aceleración centrípeta que puede experimentar el auto sin volcar es 5 m/s², determine la máxima rapidez tangencial con que puede dar la curva circular. Considere que el radio de la curvatura de la trayectoria es de 20 m.
A) 8 m/s
B) 2 m/s
C) 20 m/s
D) 15 m/s
E) 10 m/s
Rpta. : "E"
PREGUNTA 22 :
El disco de vinilo fue un medio de almacenamiento de sonido analógico muy usado en la década de los 80. Tenía un diámetro de 30 cm y frecuencia 33 RPM. Este disco ha sido ya superado por los digitales, como el disco compacto de menor tamaño y mayor almacenamiento. Respecto al disco de vinilo, determine la rapidez tangencial, en cm/s, de un punto ubicado a 5 cm del borde del disco.
A) 10𝛑
B) 11𝛑
C) 12𝛑
D) 15𝛑
E) 18𝛑
Rpta. : "B"
PREGUNTA 23 :
En una feria de diversiones, el juego del carrusel para niños presenta un periodo de 8 s. Este periodo constante se logra debido a las rotaciones constantes que ejercen los motores eléctricos con las fajas de transmisión. Si un niño está en un caballito del carrusel a 2,5 m del eje de rotación, calcule la rapidez lineal que experimenta el niño en m/s.
A) 5𝛑/7
B) 5𝛑/4
C) 5𝛑/2
D) 3𝛑/2
E) 5𝛑/8
Rpta. : "E"
PREGUNTA 24 :
Una plataforma circular rota uniformemente respecto de su centro a razón de 20 vueltas por minuto. Determine su rapidez tangencial de un punto ubicado a 40 cm de la periferia del disco. Considere que el disco tiene 1 m de radio.
A) 0,4𝛑 m/s
B) 0,2𝛑 m/s
C) 0,1𝛑 m/s
D) 0,5𝛑 m/s
E) 0,3𝛑 m/s
Rpta. : "A"
PREGUNTA 25 :
El disco versátil digital, más conocido como DVD, es un tipo de disco óptico para almacenar datos. Es idéntico al de un disco compacto, aunque contiene hasta 15 veces más información y puede transmitirla a la computadora unas 20 veces más rápido que un CD-ROM. Si consideramos que su diámetro es de 120 mm y tiene una velocidad angular de 600 RPM, entonces la magnitud de la aceleración de un punto en su periferia será
A) 245 m/s²
B) 236,87 m/s²
C) 340,5 m/s²
D) 384,72 m/s²
E) 205 m/s²
Rpta. : "B"
SEGUNDA PRACTICA
PROBLEMA 1 :
Respecto a las cantidades cinemáticas angulares, responder verdadero (V) o falso (F).
I) La posición angular es un vector cuyo sentido se determina con la regla de la mano derecha.
II) La velocidad angular es un vector paralelo al plano de giro.
III) En el movimiento circular la aceleración angular siempre es paralela a la velocidad angular.
A) VVV
B ) VVF
C) FFV
D) FVF
E) FFF
PROBLEMA 2 :
Marque la secuencia correcta luego de determinar si la proposición es verdadera (V) o falsa (F).
I) En el movimiento circular el módulo del vector posición respecto al centro de la trayectoria permanece constante.
II) En el movimiento circular, la velocidad y la velocidad angular permanecen perpendiculares entre si.
III) Si una partícula se mueve en una circunferencia, su aceleración media no puede ser nula.
A) VVV
B) FVV
C) VFV
D) VVF
E) FFF
PROBLEMA 3 :
Un auto es capaz de recorrer uniformemente 200m en 5s, si el radio de sus llantas es 0,4m. Determinar su velocidad angular durante el movimiento.
A) 2rad/s
B) 20rad/s
C) 200rad/s
D)100rad/s
PROBLEMA 4 :
Los puntos periféricos de un disco se mueven con una rapidez de 10 m/s, en tanto que los puntos ubicados a 2m de la periferia se mueven con una rapidez de 6m/s. Determine el radio de la rueda (en m).
A) 1,5
B) 2,5
C) 3,5
D) 5
E) 7,5
PROBLEMA 5 :
Respecto a las cantidades cinemáticas angulares, identifique el número de proposiciones correctas:
I) Facilitan el estudio del movimiento circular.
II) El desplazamiento angular es igual a la longitud de arco.
III) La velocidad angular media es la rapidez con que cambia la posición angular en un intervalo de tiempo.
IV) La aceleración angular media es la rapidez con que cambia la velocidad de la partícula en un intervalo de tiempo.
A) Todas
B) 3
C) 2
D) 1
E) ninguna
PROBLEMA 6 :
Con respecto a las cantidades cinemáticas angulares se puede afirmar que:
I) Todas las cantidades cinemáticas angulares son vectoriales.
II) El sentido de la aceleración angular se obtiene con la regla de la mano derecha.
III) La velocidad angular y la aceleración angular son siempre colineales.
A) VVV
B) VVF
C) VFV
D) FFV
E) FFF
PROBLEMA 7 :
Respecto a las cantidades cinemáticas angulares, ¿cuáles de las siguientes proposiciones son verdaderas?.
I) El módulo del desplazamiento es proporcional al desplazamiento angular de la partícula.
II) La velocidad angular media es proporcional al desplazamiento angular.
III) Solamente en el caso de MCU se tiene que V=ω×r .
A) VVV
B) VVF
C) FVV
D) FVF
E) FFF
PROBLEMA 8 :
¿Cuántas de las siguientes proposiciones son verdaderas respecto al movimiento circular?
I) El desplazamiento angular es un vector perpendicular al plano de la trayectoria.
II) En ciertos movimientos circulares la aceleración centrípeta puede ser cero.
III) La velocidad angular determina el plano de movimiento.
IV) La magnitud del vector posición con respecto al centro de giro se mantiene constante.
V) La velocidad tangencial se define específicamente para los movimientos circulares.
VI) Siempre es válida la ecuación △S=R△θ
A) 6
B) 5
C) 3
D) 2
E) Ninguna
PROBLEMA 9 :
Una partícula se desplaza en una trayectoria circular de 2m de radio en donde su posición angular varía con el tiempo de acuerdo a la ecuación θ=2+2t .
Si θ se mide en radianes y t en segundos, determine:
I) Su desplazamiento entre t1=1s y t2=3s.
II) Su rapidez angular media en el mismo intervalo de tiempo.
A) 4 y 8
B) 3 y 6
C) 8 y 5
D) 8 y 2
E) 5 y 2
PROBLEMA 10 :
Un ciclista que viaja en la dirección N60° E a 35km/h, aplica los frenos deteniéndose luego de 4s. Determine la dirección del vector aceleración angular.
A) E30°S
B) E20°S
C) o30°S
D) S30°E
E) S60°E
CLAVES – RESPUESTAS : 1)C 2)D 3)D 4)D 5)C 6)D 7)E 8)B 9)D 10)E
¿Qué es el movimiento circular uniforme y sus características?
El MCU es aquel movimiento circunferencial en el cual el móvil recorre desplazamientos angulares iguales en tiempos iguales.
Este movimiento se desarrolla de esta forma debido a que experimenta una velocidad angular constante.
Se cumple:
☛ En intervalos de tiempos iguales, los recorridos son iguales.
☛ En iguales intervalos de tiempo, los ángulos barridos por el radio de giro son iguales
☛ Una partícula que desarrolla un M.C.U, posee una velocidad de módulo constante.
☛ Si dos o más partículas giran en base a un mismo centro, sus velocidades angulares serán iguales.
☛ El M.C.U. es aquel movimiento de trayectoria circunferencial en el cual la rapidez tangencial permanece constante.
Es fácil darse cuenta, que hay una semejanza entre el M.C.U. y el M.R.U., si cambiamos a θ por d y ω por V
Por eso para resolver los problemas, debemos considerar esa semejanza, y para ello graficaremos como si se tratara de un movimiento rectilíneo.
APRENDIZAJES ESPERADOS
☛ Conocer los elementos del movimiento circular uniforme
☛ Identificar el M.C.U. y las ecuaciones que se emplean en este movimiento.
☛ Describir el movimiento de rotación y su relación con el movimiento circunferencial.
En la naturaleza los diversos movimientos son por lo general curvilíneos y en particular circunferenciales, este tipo de movimiento lo observamos en las hélices de un helicóptero, en la rueda de la fortuna, en los engranes del motor, etc.
¿Qué es el movimiento circunferencial?
Es un fenómeno físico que se manifiesta cuando simultáneamente un cuerpo cambia de posición y de ángulo central respecto de un punto fijo denominado centro, permitiéndole describir una circunferencia como trayectoria.
¿Qué es el movimiento circular?
Es aquel movimiento efectuado por móvil que describe una trayectoria circular o parte de una circunferencia, como por ejemplo, la trayectoria descrita por una piedra que se hace girar atada al extremo de una cuerda.
MOVIMIENTO ROTACIONAL Y MOVIMIENTO CIRCUNFERENCIAL
El movimiento rotacional, lo experimentan los cuerpos al dar vueltas en torno a un eje que los atraviesa, el EJE DE ROTACIÓN.
Movimiento circunferencial lo experimenta solo un punto del cuerpo o una partícula, que al moverse en torno a un eje describe una trayectoria circunferencial.
Por ejemplo:
El movimiento de un satélite alrededor de la tierra, es aproximadamente un movimiento circunferencial
ELEMENTOS DEL MOVIMIENTO CIRCUNFERENCIAL
RADIO DE GIRO (R)
Su medida es igual al radio de la trayectoria circunferencial ( radio de curvatura ).
Su unidad de medida en el S.I. es el metro (m).
ÁNGULO DE GIRO (𝜽)
Es el ángulo barrido por el radio de giro de la partícula.
Su unidad de medida es el radián (rad).
RECORRIDO (𝑺)
Es la longitud de arco de circunferencia el cual coincide con el recorrido de la partícula. Su unidad de medida es el metro (m).
La relación matemática entre 𝑅, 𝜃 𝑦 𝑆 es:
𝑆 = 𝜃𝑅
VELOCIDAD TANGENCIAL
Es llamada también velocidad lineal. Es la velocidad que presenta el móvil en cada punto de su trayectoria.
La velocidad tangencial se representa por medio de un vector que siempre es tangente a la trayectoria. Al módulo de la velocidad tangencial se llama rapidez tangencial
RAPIDEZ ANGULAR
Magnitud física que mide el ángulo barrido por cada unidad de tiempo.
VELOCIDAD ANGULAR
Es la magnitud vectorial que nos indica:
Rapidez angular + Dirección
La velocidad angular se representa por medio de un vector perpendicular al plano de giro
La dirección de la velocidad angular se determina con la regla de la mano derecha.
PERIODO
Es el tiempo que emplea una partícula en realizar una vuelta.
Unidad de medida en el S.I.: segundo (s)
1 vuelta <>1 revolución<>1 ciclo.
FRECUENCIA
Es el número de vueltas que realiza una partícula, por cada unidad de tiempo.
Unidad de medida en el S.I.: Hertz o s–1
Otras unidades de frecuencia son RPS (revoluciones por segundo) y RPM ( revoluciones por minuto ).
Por ejemplo consideremos que una piedra gira con 30 RPM. Ello indica que da 30 revoluciones (vueltas) en un minuto
ACELERACIÓN CENTRÍPETA
Es la aceleración que posee todo cuerpo con M.C.U. está relacionada con el cambio de dirección de la velocidad tangencial y está dirigida hacia el centro de la trayectoria circular.
En un M.C.U. la velocidad en módulo se mantiene constante, sin embargo, continuamente cambia de dirección, por ello decimos que la velocidad es variable y debido a esta variación concluimos que el móvil experimenta aceleración.
MOVIMIENTO DE ROTACIÓN
Ahora consideremos un eje giratorio fijo en sus extremos, la polea únicamente podrá experimentar movimiento rotativo. En este caso únicamente los puntos periféricos (tangenciales) de la polea tendrán igual velocidad.
MOVIMIENTO DE TRASLACIÓN Y ROTACIÓN
Consideremos que la polea - rueda trasladándose sobre una pista áspera, en cada uno de los puntos periféricos (A, B y C), acá el centro de la polea de radio ‘‘R’’ se traslada con una velocidad ‘‘V’’ y ella gira con una velocidad angular .
Cuando un disco, polea, rueda o engranaje posee un movimiento de rotación uniforme con respecto a un eje perpendicular que pasa por su centro, todos los puntos rotan con la misma velocidad angular.