TRIGONOMETRÍA ADMISIÓN CATÓLICA DESARROLLADA
PREGUNTA 31 :
Se tienen dos ángulos que sumados son 5𝛑/4 rad y su diferencia es 75°. Determina el suplemento del mayor de los ángulos en radianes.
A) 𝛑/12 rad
B) 𝛑/6 rad
C) 𝛑/4 rad
D) 𝛑/3 rad
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 32 :
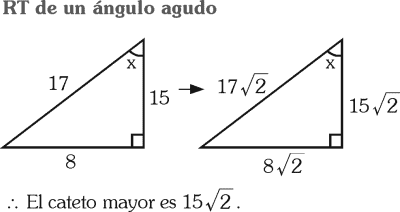
En un triángulo rectángulo, la tangente de uno de sus ángulos agudos es 8/15. Determina su cateto mayor si la hipotenusa es 17√2 .
A) 12√2
B) 10√2
C) 15√2
D) 8√2
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 33 :
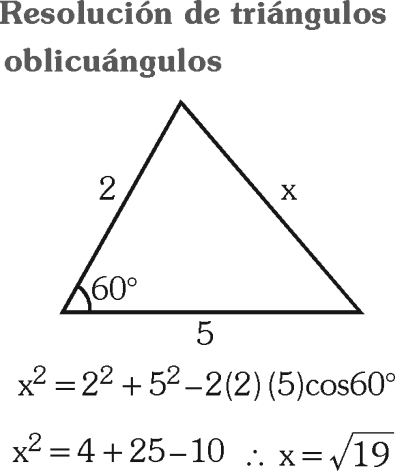
Del gráfico, determina “x”.
A) √11
B) √13
C) √17
D) √19
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 34 :
Calcula:
A) 1/11
B) 1/44
C) 19/44
D) 19/11
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 35 :
Si: cosx.ctgx=3
determina cscx – senx.
A) 1
B) 2
C) 3
D) 4
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 36 :
Si se cumple
ctgx+tgx+csc2x=4
Determina :
A) 1/7
B) 7
C) 3
D) 2
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 37 :
M=cos(θ)cos(2θ)cos(3θ)cos(4θ)csc(5θ)
Halla 64M, si θ=15°
A) √6
B) 1
C) 8√6
D) 8
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 38 :
Si 0 <x< 𝛑/2
calcula:
cos(x+𝛑)+cos(x+𝛑/2)+cos(x–𝛑)+tg(x+𝛑)cos(x+𝛑)
A) senx – 2cosx
B) 3senx
C) 2senx
D) –2senx – 2cosx
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 39 :
Halle el rango de la función
F(x)=sen²x+2senx+π
A) [π; π+3]
B) [π−1; π+3]
C) [π−1; π+4]
D) [π+1; π+3]
RESOLUCIÓN :
Agregando y quitando 1 :
F(x)=sen²x+2senx+1+π−1
⇒ F(x)=(senx+1)²+π−1
⇒ −1 ≤ senx ≤ 1
⇒ 0 ≤ senx+1 ≤ 2
⇒ 0 ≤ (senx+1)² ≤ 4
⇒ π ≤ (senx+1)²+π ≤ 4+π
⇒ π −1 ≤ (senx+1)²+π−1 ≤ 4+π−1
⇒ π−1 ≤ F(x) ≤ π + 3
Rpta. : "B"
PREGUNTA 40 :
Si x∈[40°;290°], indica el número de soluciones en dicho intervalo de:
2√3–2√3cos²x=sen2x
A) 1
B) 2
C) 3
D) 4
RESOLUCIÓN :
Ecuaciones trigonométricas
Factorizando 2√3 :
2√3(1–cos²x)=2senxcosx
⇒ 2√3sen²x=2senxcosx
I) senx=0 → x=0°, 180°, 360°
II) √3senx=cosx → tanx=√3/3
∴ x=30°; 210°
⇒ x1=180° ; x2=210° dos soluciones
Rpta. : "B"
