ANÁLISIS DIMENSIONAL EJERCICIOS RESUELTOS PDF
Los conceptos básicos de la Física se definen en función de las medidas, el objetivo de las teorías es el de establecer relaciones entre resultados de las medidas .
Iniciamos nuestro estudio de la física explicando algunas de las magnitudes físicas y algunas normas que han sido aceptadas para medirlas.
- CLIC AQUÍ Ver MAGNITUDES FÍSICAS EJERCICIOS RESUELTOS
- Ver FÓRMULAS DIMENSIONALES
- Ver PRINCIPIO DE HOMOGENEIDAD DIMENSIONAL
¿Qué es análisis dimensional?
Es la parte de la FÍSICA que estudia las relaciones entre las magnitudes fundamentales y derivadas, en el Sistema Internacional de Unidades, se considera siete magnitudes fundamentales.
¿Cuáles son las magnitudes fundamentales de la física?
Las magnitudes fundamentales son : longitud , masa , tiempo , temperatura , intensidad de corriente eléctrica , intensidad luminosa y cantidad de sustancia.
¿Cuáles son las magnitudes derivadas de la física?
Las magnitudes derivadas son : área , volumen , densidad , velocidad , aceleración , fuerza , trabajo , potencia , energía , etc.
¿Cuál es la importancia del análisis dimensional ?
☛ Sirve para expresar las magnitudes derivadas en función de las fundamentales.
☛ Se emplea para la deducción de nuevas fórmulas.
☛ Sirve para comprobar la veracidad de una fórmula física.
EJERCICIO 1
Indique verdadero (V) o falso (F) en cada proposición:
I) El calor y el trabajo mecánico tienen igual ecuación dimensional.
II) La velocidad angular y la frecuencia tienen la misma ecuación dimensional.
III) El peso y la masa tiene igual ecuación dimensional.
IV) El impulso y la cantidad de movimiento tienen diferente ecuación dimensional.
A) VVFF
B) FFVV
C) VFFF
D) FVFV
E) VFVF
Resolución
I. El trabajo y el calor según el S. I. se miden en joule por lo tanto tienen la misma ecuación dimensional. (verdadero)
II. A pesar que la unidad de la velocidad angular es rad/s y de la frecuencia es s–1 si tienen la misma ecuación dimensional por que el ángulo no es considerado cantidad física. (verdadero)
Rpta. : "A"
EJERCICIO 2
En el movimiento de un bote sobre agua, se ha determinado que la fuerza de resistencia que ejerce el agua sobre el bote es proporcional a su velocidad. Determine la ecuación dimensional de la constante de proporcionalidad.
A) LT–2
B) LT–1
C) MLT–2
D) MLT–1
E) MT–1
Resolución
Rpta. : "E"
PRIMERA PRACTICA
PREGUNTA 1 :
Respecto a las magnitudes físicas, indique cual si es fundamental.
A) área
B) energía
C) velocidad
D) temperatura
E) presión
Rpta. : "D"
PREGUNTA 2 :
Determine la veracidad (V) o falsedad (F) de las siguientes proposiciones.
I) Para medir la fuerza de atracción de la Tierra, es necesario especificar la dirección.
II) Las magnitudes escalares requieren modulo y dirección.
III) El tiempo transcurre en una determinada dirección.
A) VVV
B) VFF
C) VFV
D) FFV
E) FVF
Rpta. : "B"
PREGUNTA 3 :
Indique la secuencia correcta de verdadero (V) o falso (F).
I) Las magnitudes escalares tienen dirección.
II) La suma vectorial, es una suma numérica.
III) La suma de una magnitud escalar con una magnitud vectorial da por resultado una magnitud escalar.
A) FFV
B) FFF
C) FVV
D) VVV
E) VVF
Rpta. : "B"
PREGUNTA 4 :
De la siguiente relación de magnitudes físicas, ¿Cuántas son escalares?
• Fuerza
• Temperatura
• Tiempo
• Desplazamiento
• Densidad
A) 1
B) 2
C) 3
D) 4
E) 5
Rpta. : "C"
PREGUNTA 5 :
De la siguiente lista de magnitudes, señale cuantos son vectoriales.
• Temperatura
• desplazamiento
• Aceleración
• fuerza
• Energía
• densidad
• Velocidad
• volumen
A) 2
B) 6
C) 5
D) 3
E) 4
Rpta. : "E"
PREGUNTA 6 :
Se muestra una lista de magnitudes físicas.
• Velocidad
• Longitud
• Volumen
• Intensidad de corriente eléctrica
• Aceleración
• Masa
• Área
• Tiempo
Indique la secuencia correcta de verdad (V) o falsedad (F).
I. Solo 5 son escalares
II. Solo 2 son vectoriales
III. Solo 4 son fundamentales
A) VFV
B) VVF
C) FVF
D) FVV
E) FFV
Rpta. : "D"
PREGUNTA 7 :
La fórmula mostrada es dimensionalmente correcta. Indique las unidades de p.
A=B+pt
Donde: B es distancia (m), t es tiempo (s).
A) m/s²
B) (m/s)²
C) m/s
D) m.J
E) kg.m
Rpta. : "C"
PREGUNTA 8 :
La ecuación mostrada es dimensionalmente correcta.
Determine la magnitud A.
P=AB
Donde: P es N.s y B es m/s.
A) tiempo
B) longitud
C) masa
D) fuerza
E) aceleración
Rpta. : "C"
PREGUNTA 9 :
La ecuación mostrada es dimensionalmente correcta.
Determine x.
A=KBCx
Donde: A es longitud (m), K es un número, B es aceleración (m/s²)
A) tiempo
B) 1
C) longitud
D) 2
E) masa
Rpta. : "D"
PREGUNTA 10 :
Experimentalmente se ha determinado que la fuerza de sustentación que actúa sobre el ala de un avión, depende del área A del ala, de la densidad D del aire y de la rapidez v del avión. Halle el exponente de la rapidez en la ecuación que relaciona las magnitudes mencionadas.
A) –1
B) 0,5
C) 1
D) 2
E) 3
Rpta. : "D"
PREGUNTA 11 :
Determine el valor de la siguiente expresión x+y+z, si la ecuación
P=ρxgyhzes dimensionalmente correcta.
donde:
P=presión
ρ=densidad
g=aceleración de la gravedad
h=profundidad
A) 4
B) 3
C) 8
D) 2
E) 12
Rpta. : "B"
SEGUNDA PRACTICA
EJERCICIO 1 :
Al medir 8 kg, ¿qué magnitud física estamos utilizando?
A) energía
B) volumen
C) área
D) masa
EJERCICIO 2 :
No es una magnitud vectorial.
A) fuerza
B) densidad
C) velocidad
D) aceleración
E) desplazamiento
EJERCICIO 3 :
No es una magnitud escalar.
A) área
B) volumen
C) densidad
D) longitud
E) fuerza
EJERCICIO 4 :
Al medir 124 m, ¿ qué magnitud física estamos utilizando?
A) área
B) volumen
C) densidad
D) longitud
EJERCICIO 5 :
Al medir 120 s, ¿qué magnitud física estamos utilizando?
A) velocidad
B) tiempo
C) presión
D) energía
EJERCICIO 6 :
Toda magnitud física debe ser expresada mediante
A) solo un número
B) un ángulo
C) otra unidad de medida
D) solo una unidad de medida
E) un número y su unidad de medida
EJERCICIO 7 :
Es una cantidad fija de la misma naturaleza de la magnitud que se desea medir:
A) cantidad
B) magnitud física
C) número
D) magnitud derivada
E) unidad de medida
EJERCICIO 8 :
Señala las magnitudes físicas escalares.
I) masa
II) velocidad
III) energía
IV) densidad
A) I y II
B) Solo II
C) Solo IV
D) I, III y IV
E) III y IV
EJERCICIO 9 :
Indicar cuales son magnitudes físicas vectoriales:
I) volumen
II) velocidad
III) área
IV) desplazamiento
A) I y III
B) Solo II
C) Solo IV
D) II y IV
E) III y IV
EJERCICIO 10 :
No son magnitudes físicas derivadas.
I) volumen
II) velocidad
III) temperatura
IV) energía
A) Solo I
B) Solo III
C) I y II
D) I y IV
E) I, II y IV
EJERCICIO 11 :
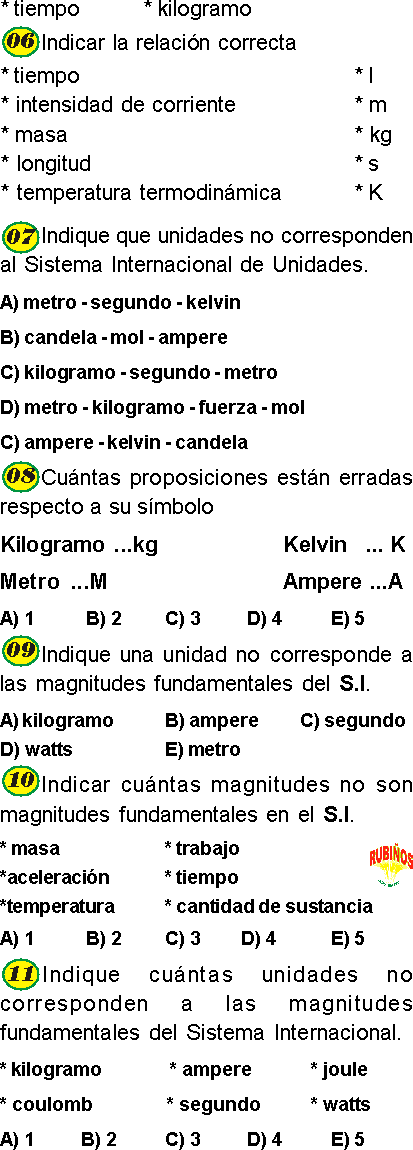
No son magnitudes fundamentales.
I) energía
II) longitud
III) potencia
IV) intensidad de corriente
V) cantidad de sustancia
A) Solo I
B) II y III
C) I y II
D) II, IV y V
E) I y III
EJERCICIO 12 :
Toda magnitud física escalar debe ser expresada mediante
I) un ángulo.
II) un número.
III) una dirección.
IV) una unidad de medida.
A) Solo I
B) Solo II
C) Solo III
D) Solo IV
E) II y IV
EJERCICIO 13 :
La temperatura del aula en el verano es 200 kelvin, ¿cuál es la representación correcta del símbolo de la unidad de medida?
A) 200 k
B) 200 kel
C) 200 K.
D) 200 K
E) 200
EJERCICIO 14 :
Kelvin La masa de un estudiante es 27 kilogramos, ¿cuál es la representación correcta del símbolo de la unidad de medida?
A) 27 kgs
B) 27 kilo
C) 27 Kg.
D) 27 kg
E) 27 kgr
EJERCICIO 15 :
Indica qué unidad(es) no corresponden al SI.
I) gramo
II) ampere
III) pulgada
V) kilogramo
V) libra
A) Solo I
B) II y IV
C) Solo IV
D) I III y V
E) III y V
EJERCICIO 16 :
Indica qué relación(es) son correctas en el Sistema Internacional.
I) kilogramo – kgs
II) candela – cd
III) ampere – A
IV) metro – mt
V) mol – moles
A) Solo II
B) Solo III
C) III y IV
D) II y III
E) I y IV
EJERCICIO 17 :
Indicar qué grupo(s) de unidades no corresponden al Sistema Internacional:
I) ampere, candela, metro
II) celsius, libra, pulgada
III) segundo, mol, kelvin
A)Solo I
B)Solo II
C)Solo III
D)Solo I y II
E)Solo II y III
EJERCICIO 18 :
Indica cuál(es) de las siguientes relaciones no son correctas según el SI:
I) presión – pascal – Pa
II) temperatura – celsius – C
III) longitud – metro – mts.
IV) potencia – coulomb – C
V) intensidad de corriente – ampere – A
A) solo II
B) solo III
C) solo V
D) II, III y IV
E) I, III y V
EJERCICIO 19 :
Indica qué relaciones están correctamente escritas en el SI.
I) 20 segundos – 20 s
II) 150 newton – 150 N
III) 5 moles – 5 mol
IV) 15 joule – 15 J
A) I y II
B) II y III
C) III y IV
D) I, II y IV
E) todas
EJERCICIO 20 :
¿Cuál de las siguientes unidades no corresponden al SI?
I) minuto
II) ohm
III) milímetro
IV) watt
V) volt
A) solo I
B) solo III
C) I y III
D) II y IV
E) II, IV y V
EJERCICIO 21 :
Indica qué magnitudes no son escalares.
I) masa
II) velocidad
III) energía
IV) densidad
A) solo I y II
B) solo II
C) solo IV
D) solo I , III y IV
E) solo III y IV
EJERCICIO 22 :
Toda magnitud física vectorial debe ser expresada mediante
I) un ángulo.
II) un número.
III) una dirección
IV) una unidad de medida.
A) solo I
B) I, III y IV
C) solo III
D) todas
E) solo II y IV
OBJETIVOS DEL APRENDIZAJE :
Al finalizar la unidad, el alumno será capaz de :
☛ Reconocer , diferenciar e interrelacionar las diferentes clases de magnitudes
☛ Conocer las magnitudes y el uso correcto del Sistema Internacional de Unidades
☛ Conocer reglas y propiedades para el uso correcto de las Ecuaciones dimensionales
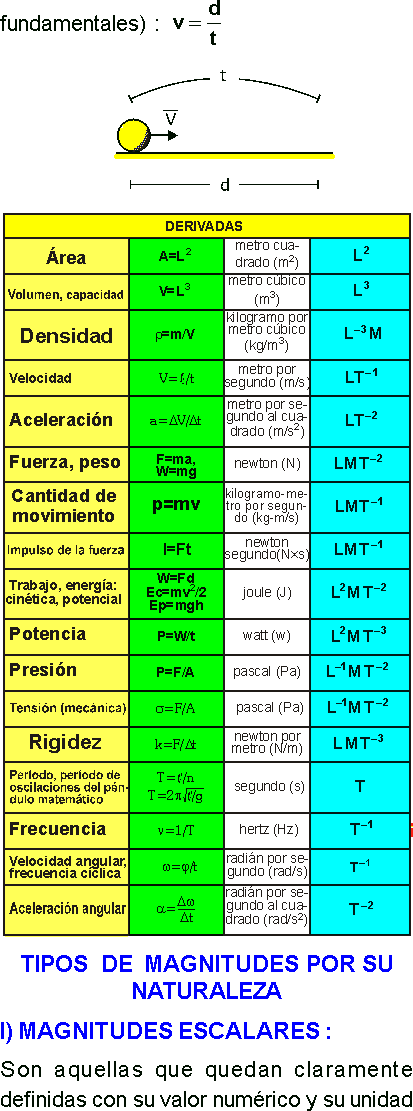
FÓRMULA DIMENSIONAL
Es aquella igualdad matemática que muestra la relación que existe entre una magnitud derivada y las magnitudes fundamentales.
La dimensión de una magnitud física se representa del siguiente modo:
Sea A la magnitud física.
[A]: se lee, dimensión de la magnitud física A.
FÓRMULAS DIMENSIONALES BÁSICAS
[Longitud] = L
[Masa] = M
[Tiempo] = T
[Temperatura] = θ
[Intensidad de la corriente eléctrica]=I
[Intensidad luminosa] = J
[Cantidad de sustancia] = N
[Número] = 1
[Área] = L2
[Volumen] = L3
[Densidad] = ML–3
[Velocidad] = LT–1
[Aceleración] = LT–2
[Fuerza] = MLT–2
[Trabajo] = ML2T–2
[Energía] = ML2T–2
[Potencia] = ML2T–3
[Presión] = ML–1T–2
[Período] = T
[Frecuencia] = T–1
[Velocidad angular] = T–1
[Ángulo] = 1
[Caudal] = L3T–1
[Aceleración angular] = T–2
[Carga eléctrica] = IT
[Iluminación] = JL–2
PRINCIPIO DE HOMOGENEIDAD DIMENSIONAL
En una fórmula física, todos los términos de la ecuación son dimensionalmente iguales.
CASOS ESPECIALES
PROPIEDADES DE LOS ÁNGULOS
Los ángulos son números, en consecuencia, la dimensión de los ángulos es igual a la unidad.
PROPIEDAD DE LOS EXPONENTES
Los exponentes son siempre números, por consiguiente la dimensión de los exponentes es igual a la unidad.
PROPIEDAD DE ADICIÓN Y SUSTRACCIÓN
En las operaciones dimensionales no se cumplen las reglas de la adición y sustracción.
L + L = L
M – M = M
FÓRMULAS EMPÍRICAS
Son aquellas fórmulas físicas que se obtienen a partir de datos experimentales conseguidos de la vida cotidiana o en el laboratorio de ciencias.
ECUACIONES DIMENSIONALES
Son aquellas relaciones de igualdad en donde algunas magnitudes físicas son conocidas y otras, o no lo son, o tienen dimensiones desconocidas.
Veamos los siguientes ejemplos:
• L³M[X] – L³[Y] = L³MT−¹
Incógnitas: [X], [Y] (Magnitudes)
• L4T3θ–2 =LsTrθ2r–u
Incógnitas: r, s, u (Números)
REGLAS IMPORTANTES
I) Las magnitudes físicas así como sus unidades no cumplen con las leyes de adición o sustracción, pero sí con las demás operaciones aritméticas.
Veamos los siguientes ejemplos:
• L²+L²+L² = L²
• LT–2 – LT–2=LT–2
II) Todos los números en sus diferentes formas con cantidades adimensionales, y su fórmula dimensional es la unidad.
Veamos los siguientes ejemplos:
[√2]=1
[Sen30°]=1
[2𝛑rad]=1
[Log5]=1
CANTIDAD ADIMENSIONAL:
Es aquella que carece de dimensiones, es decir el exponente de las magnitudes fundamentales en la fórmula dimensional es cero (0).
De este modo se tiene que la fórmula dimensional de una cantidad adimensional es:
[Cantidad adimensional] = 1
Entre ellas tenemos: los números reales, las funciones numéricas como las funciones trigonométricas, logarítmicas, exponenciales,... etc.
Asimismo los ángulos planos y los ángulos sólidos expresados en radianes y estereoradianes respectivamente, están en la lista de cantidades adimensionales.
INTRODUCCIÓN
Sabemos que la madre de la sabiduría es la curiosidad y todo aquel que se deleite con el mundo de la Física; deberá ser observado para comprender estos fenómenos .
Sin embargo una observación científica por lo general esta incompleta sí no se expresa de manera cuantitativa , así que para obtener tal información debe hacerse la medición de una cantidad física , por tanto, las mediciones conforman buena parte de la rutina de un físico experimental.
Lord Kelvin decía que nuestro conocimiento es satisfactorio sólo después de expresarlo en números.
Para la física y la química , en su calidad de ciencias experimentales , la medida constituye una operación fundamental .
Sus descripciones del mundo físico se refieren a magnitudes o propiedades medibles .
Las unidades , como cantidades de referencia a efectos de comparación , forman parte de los resultados de las medidas .
Cada dato experimental se acompaña de su error o al menos se escriben sus cifras de tal modo que reflejen la precisión de la correspondiente medida.
Se consideran ciencias experimentales a aquellas que por sus características y particularmente por el tipo de problemas de los que se ocupan , pueden someter sus afirmaciones o enunciados al juicio de la experimentación .
En un sentido científico la experimentación hace alusión a una observación controlada ,en otros términos experimentar es reproducir en el laboratorio el fenómeno en estudio con la posibilidad de variar a voluntad y de forma precisa las condiciones de observación .
La física y la química constituyen ejemplos de ciencias experimentales .