LOS VECTORES EN FÍSICA EJERCICIOS RESUELTOS PDF
¿Qué es un vector?
Es un ente matemático que gráficamente se representa por un segmento de recta orientado.
La física utiliza los vectores para representar las magnitudes vectoriales.
¿Para que sirven los vectores?
El estudio de los vectores tiene una gran relevancia , puesto que a través de ellos se representan las magnitudes vectoriales, las cuales nos permitirán describir y comprender mejor los fenómenos físicos.
En ese sentido, el concepto de vector se estableció para poder describir matemáticamente el espacio en el que vivimos todos los vectores, como la fuerza, velocidad y aceleración están relacionados con el espacio.
Todos los fenómenos físicos se desarrollan en el espacio; por ello, para describir correctamente un fenómeno físico se requiere necesariamente el uso de vectores.
APRENDIZAJES ESPERADOS :
☛ Representar algunos fenómenos físicos, empleando modelos vectoriales.
☛ Comprender y aplicar correctamente las reglas existentes para las operaciones con vectores.
☛ Conocer el método del triángulo y del polígono para calcular la resultante de un conjunto de vectores .
☛ Aprender la descomposición y composición rectangular de los vectores.
MÉTODOS PARA CALCULAR LA RESULTANTE
MÉTODO DEL PARALELOGRAMO
Se utiliza para calcular la resultante de dos vectores concurrentes y coplanares que tienen un mismo punto de origen.
Gráficamente se construye un paralelogramo trazando paralelas a los vectores.
El vector resultante se traza uniendo el origen de los vectores con la intercepción de las paralelas.
Módulo de R :
R² = A² + B² + 2ABCosα
MÉTODO DEL TRIÁNGULO
Se utiliza para calcular la resultante de dos vectores concurrentes y coplanares que están uno a continuación del otro. Gráficamente se construye un triángulo, trazando el vector resultante desde el origen del primer vector hasta el extremo del segmento vector.
Módulo de R :
R² = A² + B² – 2ABCosα
En el triángulo vectorial también se cumple la ley de senos.
a/senA =b/senB=c/senC
MÉTODO DEL POLÍGONO
Se utiliza para calcular la resultante de un conjunto de vectores concurrentes y coplanares.
Es un método grafico que utiliza escalas apropiadas y consiste en trazar los vectores uno a continuación del otro manteniendo sus características.
El vector resultante se traza uniendo el origen del primer vector con el extremo del último vector.
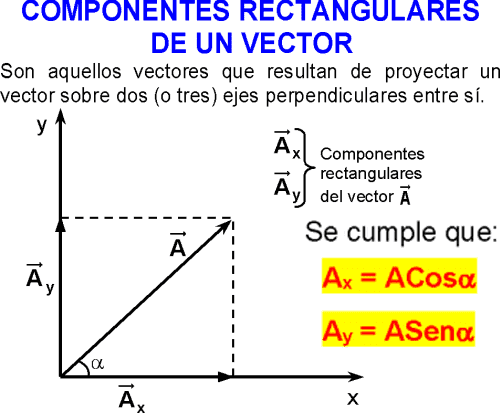
COMPONENTES RECTANGULARES DE UN VECTOR
Son aquellos vectores que resultan de proyectar un vector sobre dos (o tres) ejes perpendiculares entre sí.
Se cumple que:
Ax = ACosα
Ay = ASenα
MÉTODO DE LAS COMPONENTES RECTANGULARES
Permite calcular el módulo y la dirección de la resultante de un conjunto de vectores.
Pasos a seguir.
1° Se halla las componentes rectangulares.
2° Se calcula la resultante en cada uno de los ejes coordenadas (Rx ; Ry)
3° Se calcula el módulo de la resultante aplicando Pitágoras y su dirección aplicando la función tangente.
DEFINICIÓN DE VECTOR
Es un elemento matemático que se manifiesta a través de 2 características fundamentales: módulo y dirección.
REPRESENTACIÓN GRÁFICA
PROPIEDADES FUNDAMENTALES DE LOS VECTORES
I) La suma ó la diferencia de dos ó más vectores siempre dará como resultado otro vector.
II) Para que dos ó más vectores sean iguales necesariamente deben tener todos el mismo módulo, dirección y sentido.
III) Todo vector puede cambiar de sentido, cambiándole únicamente el signo.
IV) Todos los vectores colineales y/o paralelos, pueden sumarse y/o restarse como simples números reales, ya que poseen el mismo vector unitario.
V) Todos los vectores no paralelos ni colineales no se pueden sumar directamente puesto que la suma aritmética no es igual a la suma vectorial en este caso.
VI) El vector resultante de dos o más vectores no paralelos ni colineales se determina ubicando los vectores uno a continuación de otro, determinando estos una poligonal abierta que luego esta poligonal será cerrada por el vector resultante.
EJERCICIO 1 :
La suma de dos vectores mide 14 y la suma mínima mide 2. Calcula el módulo de los vectores.
a) 14 y 2
b) 7 y 7
c) 8 y 5
d) 6 y 8
e) 10 y 4
Rpta. : "D"
EJERCICIO 2 :
La suma de dos vectores es 16 y la suma mínima es 0. Calcula la resultante cuando formen 90°.
A) 8
B) 4
C) 8√2
D) 16
E) 16√2
Rpta. : "C"
EJERCICIO 3 :
La resultante de dos vectores que forman 90° es 10. Además, la suma máxima de ambos es 14. Calcula la suma mínima de los vectores si son enteros y pares consecutivos.
A) 4
B) 6
C) 2
D) 0
E) 8
Rpta. : "C"
EJERCICIO 4 :
Si la resultante máxima de dos vectores es 28 y la resultante mínima es 4. Calcula el módulo de la resultante cuando formen un ángulo de 90°.
A) 10
B) 8
C) 15
D) 20
E) 16
Rpta. : "D"
EJERCICIO 5 :
Si la resultante de dos vectores que forman 90° es 50u. Calcula la suma máxima de los vectores si además la resultante mínima de dichos vectores es 34 además son enteros y su cociente es 7/24.
A) 62
B) 31
C) 48
D) 14
E) 42
Rpta. : "A"
EJERCICIO 6 :
Si dos vectores que forman 90° dan como resultante “R”. Calcula R si la suma máxima de los vectores es 4u, y el producto de ambos vale 3 además son impares consecutivos.
A) 3
B) 1
C) √13
D) √7
E) √10
Rpta. : "E"
EJERCICIO 7 :
Determinar el vector resultante:
RESOLUCIÓN :
Rpta. : "B"
Ordinariamente usamos la palabra "modelo" para referirnos a una réplica en menor escala (digamos, de un ferrocarril) o a una persona que exhibe ropa (o se exhibe sin ropa).
En física, un modelo es una versión simplificada de un sistema físico que sería demasiado complejo si se analizase de forma detallada.
Al usar un modelo para predecir el comportamiento de un sistema, la validez de las predicciones está limitada por la validez del modelo. La predicción de Galileo respecto a la caída de los cuerpos corresponde a un modelo idealizado que no incluye la resistencia del aire. El modelo funciona bien para una bala de cañón, pero no para una pluma.
Algunas cantidades físicas, como tiempo, temperatura, masa, densidad y carga eléctrica, se pueden describir plenamente con un número y una unidad, pero muchas otras cantidades importantes tienen asociada una dirección y no pueden describirse por un solo número. Tales cantidades tienen un papel esencial en muchas áreas centrales de la física, como el movimiento y sus causas, y los fenómenos de la electricidad y el magnetismo. Un ejemplo sencillo es el movimiento de un avión: para describirlo plenamente, debemos indicar no sólo qué tan rápidamente se mueve, sino también en qué dirección.
Para ir de Lima a Cuzco, un avión debe ir al este, no al sur. La rapidez del avión combinado con su dirección constituyen una cantidad llamada velocidad. Otro ejemplo es la fuerza, que en física es un empuje o atracción aplicado a un cuerpo.
Para describir plenamente una fuerza hay que indicar no sólo su intensidad, sino también en qué dirección tira o empuja. Es verdaderamente importante que reconozcas que en nuestra naturaleza algunos fenómenos físicos requieren algo más que números y unidades físicas para quedar plenamente explicados.
Te preguntarás
¿Qué se puede usar, además de los números y unidades, para detallar los fenómenos?.
La respuesta es el vector, y las magnitudes físicas que lo necesitan se llaman magnitudes vectoriales , las mismas que tienen en esencia dos características especiales:
Tienen
dirección y sentido : Cuando decimos que un alumno experimenta un desplazamiento de 5m, debemos agregar desde dónde y hacia dónde. Sin estos datos no podríamos imaginar el movimiento.
No cumplen con las leyes de la adición de números reales :
Si decimos que dos personas empujan un mismo cuerpo con fuerzas iguales de 15 newtons, sin indicar la dirección y sentido de cada uno, el resultado puede ser variable.
Así por ejemplo:
Si se aplican los dos hacia un mismo lado, el resultado será equivalente a aplicar una fuerza de 30 newtons. Sin embargo, si estas fuerzas se aplican en una misma recta pero en sentidos opuestos, el resultado sería como no aplicar fuerzas. Así pues, la resultante de las fuerzas depende de la orientación de éstas.
HISTORIA
Las nociones de vectores están implícitamente contenidas en las reglas de composición de las fuerzas y de las velocidades, conocidas hacía el fin del siglo XVII.
Es en relación con la representación geométrica de los números llamados imaginario, como las operaciones vectoriales se encuentran por primera vez implícitamente realizadas, sin que el concepto de vector este aún claramente definido. Fue mucho más tarde, y gracias al desarrollo de la geometría moderna y de la mecánica, cuando la noción de vector y de operaciones vectoriales se concretó.
El alemán Grassman, en 1844, por métodos geométricos introdujo formalmente las bases del cálculo vectorial ( suma, producto escalar y vectorial).
El inglés Hamilton, por cálculos algebraicos, llegó a las mismas conclusiones que Grassman; empleó por primera vez los términos escalar y vectorial.
Hacia el final del siglo XIX , el empleo de los vectores se generalizó a toda la física.
Bajo la influencia de los ingleses Hamilton Stokes, Maxwell y Heaviside, y del americano Gibbs (quien utilizó la notación del punto para el producto escalar y del × para el producto vectorial), se amplió el cálculo vectorial, introduciendo nociones más complejas, como los operadores vectoriales: gradiente, divergencia y rotacional.
