ARREGLOS NUMÉRICOS EJERCICIOS RESUELTOS PDF RAZONAMIENTO LÓGICO MATEMÁTICO
Los problemas sobre distribuciones numéricas consisten en ubicar en una gráfica determinada un conjunto de números (generalmente no se repiten) bajo condiciones particulares (sumas o productos constantes, garantizar sumas dadas, sumas máximas o mínimas, etc.).
El criterio de resolución es variado, dependerá de las condiciones que se brinden en el problema y de lo que se solicite hallar.
Así tenemos
☛ Parejas de números que siempre estén juntos o siempre separados, etc.
☛ Sumas o productos dados (u otras operaciones) para completar.
En algunos casos, en el problema se indicará los números por distribuir.
☛ Sumas o productos constantes o aquellos resultados que alcancen su máximo o mínimo valor sin necesidad de distribuir los números dados, sino mediante ecuaciones.
PREGUNTA 1:
Escriba en los cuadraditos de la figura los números enteros del 1 al 9, un número en cada cuadradito y, sin repetir, de tal manera que la suma de los números escritos en la fila y columna sea la misma e igual a 27. ¿Cuál es el número que se escribe en el cuadradito sombreado?
A) 9
B) 2
C) 3
D) 5
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 2 :
En el siguiente gráfico, distribuya los seis primeros números primos, de modo que las sumas en cada uno de los lados sean 21 ; 22 y 23. Halle (x+y+z).
A) 13
B) 16
C) 17
D) 15
E) 18
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 3 :
En los 12 cuadraditos pequeños se escriben todos los números enteros del 1 al 12, sin repetición, de modo que la suma de los cuatro valores escritos a lo largo de cada lado del cuadrado más grande sea la misma y la menor posible. ¿Cuál es el valor máximo de la suma de los números que están escritos en los cuadraditos sombreados?
A) 9
B) 7
C) 11
D) 3
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 4 :
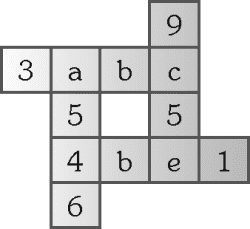
En el arreglo numérico que se muestra en la figura, se cumple que, al sumar los números de · las filas o columnas formadas por cuatro casillas, se obtiene siempre el mismo resultado. Halle el valor de b ÷ c
A) 7
B) 6
C) 5
D) 4
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 5 :
Los números del 1 al 7 pueden ocupar la posición de las letras una sola vez, de modo que: M+N+P=Q+R+S=M+X+S=P+X+Q=N +X+R=12 Halle X.
A) 2
B) 7
C) 5
D) 6
E) 4
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 6 :
En la figura, distribuya los números naturales del 1 al 9, uno en cada círculo y sin repetir, de modo que las cifras conectadas por un segmento sumen lo que se indica. Halle la suma de los dígitos ubicados en los círculos sombreados.
A) 10
B) 11
C) 12
D) 9
E) 8
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 7:
En cada círculo de la figura escriba un número entero del 2 al 11, sin repetir, de modo que en cada tres círculos dispuestos en línea recta y unidos por flechas, los números sumen lo mismo y sea lo menor posible. Determine la suma de los números escritos en los círculos grises.
A) 41
B) 45
C) 48
D) 40
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 8 :
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 9 :
Lewis observa que los catorce dígitos del número de su tarjeta de crédito, cumplen que la suma de tres dígitos consecutivos cualesquiera es 22. Además, observa que, de derecha a izquierda, el tercer dígito es 7, ¿cuál es el mínimo valor del último digito de su tarjeta de crédito?
A) 4
B) 3
C) 5
D) 6
E) 2
RESOLUCIÓN :
.png)



.png)















.png)
.png)
.png)





.png)


.png)

