MOVIMIENTO PARABÓLICO EJERCICIOS RESUELTOS PDF MPCL
¿Qué es movimiento parabólico y sus características?
Es aquel movimiento con aceleración constante, cuya trayectoria es una línea curva denominada parábola.
También podemos decir que este es un movimiento compuesto porque está formado por:
Eje X: MRU
Eje Y: MVCL (caída libre)
Si el vector gravedad es paralela al eje Y
Un chorro de agua saliendo de la toma de agua; las partículas incandescentes al momento de soldar ; el movimiento de una pelota en el básquet , entre otros. Aproximadamente, estas trayectorias curvas son parábolas y serán analizadas en este tema .
Veamos que ocurre al lanzar un proyectil horizontalmente
Si realizamos las consideraciones:
☛ Se desprecia la resistencia del aire, entonces diremos que el proyectil está en caída libre.
☛ La altura de lanzamiento es pequeña comparada con el radio de la tierra
☛ Cerca a la superficie terrestre, la aceleración de la gravedad , es constante en módulo y dirección (dirigida hacia el centro de la Tierra ): g=9,81 m/s²
Para fines prácticos, se asumirá : g=10 m/s²
Bajo estas condiciones el cuerpo describe una curva que coincide con una PARÁBOLA.
Por ello al movimiento del proyectil, se denomina MOVIMIENTO PARÁBÓLICO DE CAIDA LIBRE o MPCL
Análisis del movimiento
☛ Se recomienda analizar en dos proyecciones mutuamente perpendiculares.
☛ El movimiento del proyectil a lo largo de la horizontal es uniforme, es decir:
Vx=constante
Por ello usaremos: dx=Vx.t
☛ Simultáneamente, en la dirección vertical, ocurre un movimiento uniformemente variado puesto que se considera constante la aceleración de la gravedad.
Entonces se usarán las ecuaciones del movimiento de caída libre o MVCL
☛ Además la velocidad en cualquier instante es tangente a la trayectoria
☛ Según Galileo Galilei, el movimiento parabólico es el resultado de la unión de dos movimientos, los cuales se realizan independiente y simultáneamente.
¿Cuáles son las fórmulas del movimiento parabólico ?
Para resolver un problema de MPCL, no hay fórmulas, se utilizan las ya conocidas del MRU (en el eje X) y las del MVCL (en el eje Y), teniendo en cuenta que el tiempo es común en ambos ejes.
APRENDIZAJES ESPERADOS :
• Conocer las fórmulas del movimiento parabólico de caída libre.
• Establecer las características del movimiento parabólico para analizar adecuadamente el movimiento que realiza un proyectil.
• Establecer el método de análisis y las ecuaciones del movimiento parabólico de caída libre.
MOVIMIENTO PARABÓLICO DE CAÍDA LIBRE (M.P.C.L.)
Es aquel movimiento cuya trayectoria es una curva llamada parábola en donde la aceleración es constante.
Si un cuerpo se lanza en forma inclinada o se lanza en forma horizontal y se mueve cerca de la tierra despreciando la resistencia del aire , realiza un movimiento parabólico de caída libre en donde su aceleración de la gravedad es constante.
El M.P.C.L. puede ser descrito como un movimiento compuesto por:
I) Un movimiento vertical de caída libre (M.V.C.L.).
II) Un movimiento horizontal a velocidad constante (M.R.U.).
Ejemplo:
Un proyectil ha sido lanzado con una velocidad de 50 m/s y formando un ángulo de 37° con la horizontal.
Si despreciamos los efectos del aire y consideramos g= 10 m/s², determine:
𝑖) El tiempo de vuelo.
𝑖𝑖) El alcance horizontal del proyectil.
Resolución:
En primer lugar describamos el movimiento que experimenta el proyectil
Examinando la proyección vertical del movimiento parabólico encontramos que: tvuelo=6s y examinando la proyección horizontal del movimiento encontramos el alcance horizontal (d) del M.R.U.
Las ecuaciones vectoriales simplifica y reduce el número de ecuaciones, cuando el punto final del movimiento está por debajo del punto inicial, además recuerda que todo vector que está dirigido hacia arriba será positivo (+), pero si está hacia abajo, será negativo (–).
En un lanzamiento parabólico se comprueba que el máximo alcance horizontal se presenta cuando el ángulo de disparo es de 45°.
Podemos decir que el MPCL es la superposición de dos movimientos : un movimiento con velocidad constante (MRU) en la distancia inicial de lanzamiento y un movimiento de un cuerpo que cae libremente en la dirección vertical con aceleración g constante (MVCL)
TIRO PARABÓLICO A PARTIR DE UN PLANO INCLINADO
En esta situación se sugiere trabajar en direcciones paralelas y perpendiculares al plano inclinado, además utilizar el ángulo del plano inclinado (a) para descomponer la aceleración de la gravedad.
MOVIMIENTO EN DOS Ó MAS DIMENSIONES
Las ecuaciones para estos tipos de movimiento con aceleración constante, serán las misma que las ecuaciones vectoriales anteriores, pero el vector estará ubicado en más de una dimensión.
PROBLEMA 1 :
Se lanza un proyectil, de tal manera que su alcance (R) es el doble de su altura máxima (Hmáx).
Calcule el ángulo a con el que fue lanzado.
A) arc tan(1/4)
B) arc tan(1/3)
C) arc tan(3)
D) arc tan(2)
E) arc tan(4)
RESOLUCIÓN :
Rpta. : "D"
PRIMERA PRACTICA PROPUESTA
PREGUNTA 1 :
Desde una torre cuya altura es de 25m. se lanza una piedra con la rapidez V0=20m/s., formando con el horizonte un ángulo de 30º. Determina el tiempo en que caerá a tierra (valor aproximado).
a) 3s
b) 2,9s
c) 3,1s
d) 2,5s
e) 4,1s
Rpta. : "D"
PREGUNTA 2 :
Un cuerpo se deja caer desde una altura de 250m respecto al piso. Cuando está descendiendo a una altura de 125m un elemento curvo modifica su trayectoria, despidiéndola horizontalmente. Qué tiempo empleará en llegar al piso.
(g =10m/s²)
a) 5s
b) 7s
c) 9s
d) 8s
e) 10s
Rpta. : "E"
PREGUNTA 3 :
Una partícula se lanza con una rapidez inicial V0=15 m/s formando un ángulo de 53° con la horizontal. ¿En qué instante “t” su rapidez formará un ángulo de 45° con la horizontal?
(g = 10 m/s²)
a) t = 0,1 s
b) t = 0,2 s
c) t = 0,3 s
d) t = 0,4 s
e) t = 0,6 s
Rpta. : "C"
PREGUNTA 4 :
La rapidez de un proyectil en el punto más alto se su trayectoria parabólica es de 40m/s. si además su alcance es de 240m, determina su rapidez inicial.
(g = 10 m/s²)
a) 30m/s
b) 40m/s
c) 50m/s
d) 45m/s
e) 25m/s
Rpta. : "C"
PREGUNTA 5 :
Desde una superficie horizontal se lanza un cuerpo con una rapidez de 100 m/s con un ángulo de 37°. Halla el tiempo de vuelo, la altura y el alcance máximo.
(g =10 m/s²)
a) 12s, 180m, 960m
b) 6s, 180m, 430m
c) 13s, 150m, 300m
d) 18s, 280m, 500m
e) 24s, 210m, 450m
Rpta. : "A"
PREGUNTA 6 :
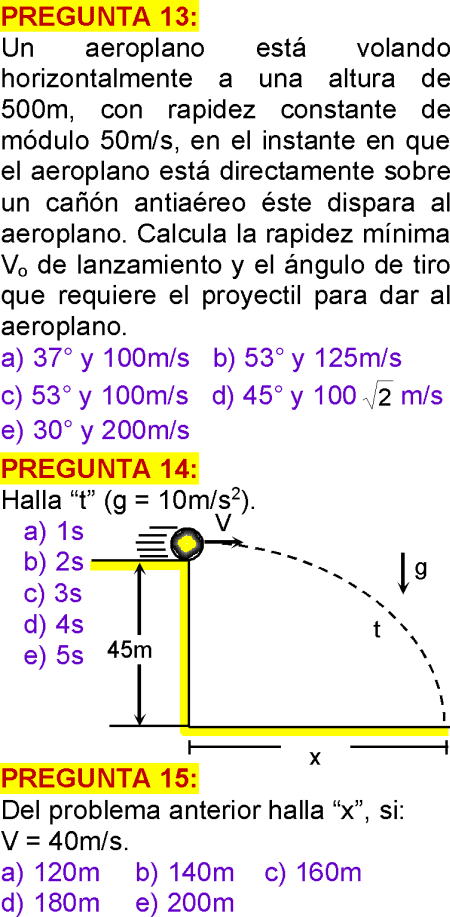
Un aeroplano está volando horizontalmente a una altura de 500m, con rapidez constante de módulo 50m/s, en el instante en que el aeroplano está directamente sobre un cañón antiaéreo éste dispara al aeroplano. Calcula la rapidez mínima V0 de lanzamiento y el ángulo de tiro que requiere el proyectil para dar al aeroplano.
a) 37° y 100m/s
b) 53° y 125m/s
c) 53° y 100m/s
d) 45° y 100 m/s
e) 30° y 200m/s
Rpta. : "B"
PREGUNTA 7 :
Dos objetos son lanzados horizontalmente en direcciones contrarias desde la misma vertical con rapideces de 20m/s y 30m/s y alturas de 80m y 45m respecto del piso respectivamente. ¿Qué distancia separa los puntos de impacto de los cuerpos en el piso?
a) 80m
b) 90m
c) 160m
d) 170m
e) 20m
Rpta. : "D"
PREGUNTA 8 :
Un cañón dispara un proyectil con una rapidez de 80√2m/s. ¿Cuál será la rapidez total del proyectil al cabo de 2 segundos, si el ángulo de lanzamiento fue 45°?
(g = 10 m/s²)
a) 80m/s
b) 60m/s
c) 70m/s
d) 100m/s
e) 120m/s
Rpta. : "D"
PREGUNTA 9 :
Un proyectil es lanzado con un ángulo de elevación de 37°. Si cuando ha ascendido las tres cuartas partes de su altura máxima, le falta 3s para llegar a su altura máxima. Calcula la rapidez de lanzamiento.
(g = 10 m/s²)
a) 50m/s
b) 60m/s
c) 70m/s
d) 80m/s
e) 100m/s
Rpta. : "E"
PREGUNTA 10 :
Un avión vuela horizontalmente con una rapidez de 150m/s a una altura de 78,4m sobre un barco que se mueve a 20m/s, en la misma dirección, pero en sentido opuesto. ¿A qué distancia del barco el avión debe soltar una bomba para que impacte en el barco?
(g = 10 m/s²)
a) 680m
b) 730m
c) 846m
d) 932m
e) 1043m
Rpta. : "A"
PREGUNTA 11 :
Dos esferas saliendo de la superficie horizontal de una mesa con rapideces de 3 y 8m/s; y caen al piso de tal manera que sus rapideces forman ángulos complementarios con el piso. Calcula la altura de la mesa.
(g =10 m/s²)
a) 1,2m
b) 1,5m
c) 1,8m
d) 2,0m
e) 0,8m
Rpta. : "A"
PREGUNTA 12 :
Desde un globo aerostático que asciende verticalmente con una rapidez de 6m/s, se lanza una piedra horizontal (respecto del globo) con una rapidez Vx = 5m/s. Si la piedra impacta en la superficie a 15m, de la vertical del globo, determina desde que altura se lanzó la piedra.
(g =10 m/s²)
a) 15m
b) 20m
c) 27m
d) 25m
e) 30m
Rpta. : "C"
PREGUNTA 13 :
¿Cuál es la diferencia entre las alturas máximas alcanzadas por un proyectil disparado con una rapidez V0 =2m/s, cuando varía su ángulo de tiro de 30° a 60°? El módulo de la rapidez de lanzamiento es constante.
(g = 10 m/s²)
b) 0,2m
c) 0,3m
d) 0,4m
e) 0,5m
Rpta. : "A"
PREGUNTA 17 :
En el movimiento parabólico no se cumple:
I. En la altura máxima la rapidez es cero.
II. La rapidez en todo instante es la suma vectorial de las rapideces de sus movimientos componentes.
III. El tiempo de vuelo, depende del ángulo de lanzamiento.
a) Sólo I
b) Sólo II
c) Sólo III
d) Sólo I y II
e) Todos
Rpta. : "A"
PREGUNTA 18 :
Un cazador inexperto apunta un objetivo, creyendo que el proyectil se movería en línea recta; para su sorpresa, luego de 0,50 s, el proyectil pasa por debajo del blanco a 2,5 m del piso. ¿A qué altura del piso estaba el blanco?
(g = 10 m/s²)
A) 2,8 m
B) 2,87 m
C) 3,0 m
D) 3,75 m
E) 3,9 m
Rpta. : "D"
PREGUNTA 19 :
De la composición de un movimiento uniforme y otro uniformemente variado resulta un movimiento cuya trayectoria es una parábola, y si además consideramos que solo actúa la fuerza de gravedad, el movimiento es de caída libre. Considere el lanzamiento de una esfera con una rapidez lo suficiente como para alcanzar un objetivo alejado horizontalmente 80 m y a 40 m por encima del piso. Si el ángulo de elevación es 37º, determine la rapidez de lanzamiento.
A) 20 m/s
B) 30 m/s
C) 40 m/s
D) 50 m/s
D) 45 m/s
Rpta. : "D"
PREGUNTA 20 :
Para lograr el máximo alcance en un tiro parabólico, se debe dar una dirección de 45° a la velocidad. Suponga este caso para el lanzamiento de un proyectil. Si se logra un alcance horizontal de 40 m, ¿cuánto es su altura máxima?
(g = 10 m/s²)
A) 5 m
B) 8 m
C) 10 m
D) 12 m
E) 15 m
Rpta. : "C"
PREGUNTA 21 :
La fuerza del aire puede dificultar el movimiento de los proyectiles, puesto que siempre actúa en dirección opuesta a la velocidad. Para tener una idea, un objeto que en caída libre logra un alcance de 2000 m, debido a la resistencia del aire solo logra desplazarse 200 m, es decir el 10 %. Suponga que un proyectil se lanza en caída libre con 100 m/s y un ángulo de elevación de 37º. Halle la relación entre su altura máxima y su alcance horizontal.
A) 3/10
B) 2/7
C) 3/16
D) 5/18
D) 7/13
Rpta. : "C"
PREGUNTA 22 :
En caída libre, los cuerpos se mueven única y exclusivamente por la acción de su peso o fuerza de gravedad. Si un objeto es lanzado horizontalmente desde el techo de un edificio de 31,25 m y logra impactar a 20 m del pie del edificio, ¿con qué rapidez se lanzó el objeto?
(g = 10 m/s²)
A) 6 m/s
B) 7 m/s
C) 6 m/s
D) 10 m/s
E) 8 m/s
Rpta. : "E"
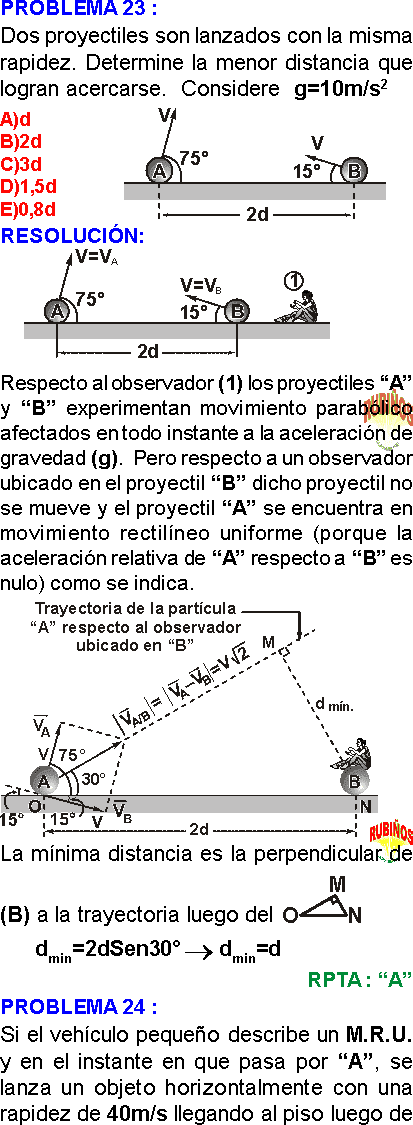
PREGUNTA 23 :
En Europa, la práctica de deportes de invierno suele ir acompañado de avalanchas y deslizamientos de nieve, por lo que, como medida de prevención, se diseñan y efectúan detonaciones controladas. Un cañón neumático lanza un proyectil sobre una zona de peligro. El cañón se mantiene formando un ángulo de 37° con la horizontal y el alcance máximo del proyectil es de 60 m. ¿Cuál es la velocidad del proyectil cuando sale del cañón?
(g = 10 m/s²)
A) 5 m/s
B) 15î +20k
C) 20î +15k
D) 25 m/s
E) 10î +25k
Rpta. : "C"
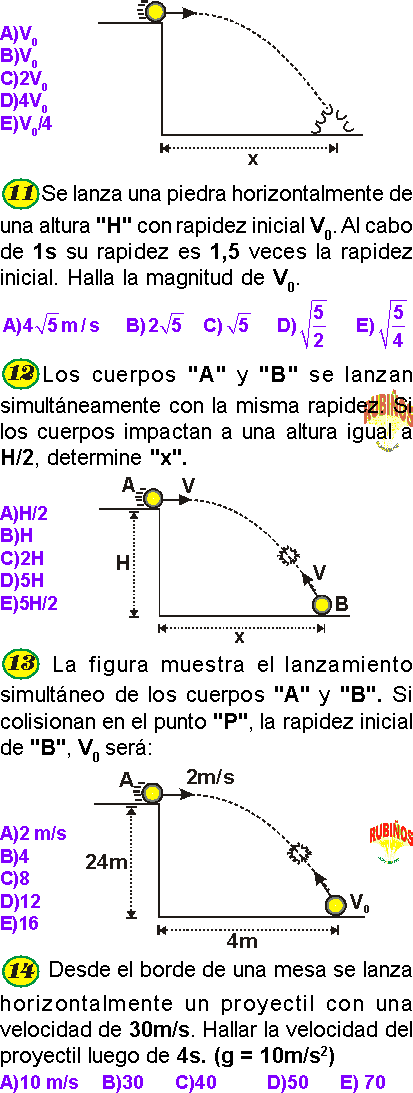
PREGUNTA 24 :
El piloto de un avión sabe que al soltar un proyectil, este por inercia saldrá con la velocidad que tiene el avión. Por ese motivo el proyectil debe ser soltado a una distancia adecuada del blanco objetivo. Un bombardero B-2 Spirit que sobrevuela con una velocidad de v = (300; 400)m/s suelta un proyectil impactando sobre un objetivo al cabo de 1,5 min. ¿A qué distancia del objetivo se soltó el proyectil?
A) 4500 m
B) 27 000 m
C) 4500√37 m
D) 3200√5 m
E) 3000√3 m
Rpta. : "C"
PREGUNTA 25 :
Cuando deseamos que un proyectil logre su máximo alcance horizontal, el ángulo de elevación de la velocidad inicial es de 45º. Es obvio que la velocidad de lanzamiento deberá procurar ser muy grande y además despreciar la resistencia del aire. Entonces un proyectil que logra un máximo alcance de 1 km, en caída libre debe ser lanzado con una velocidad de
A) (300; 400) m/s.
B) (500; 800) m/s.
C) (600; 600) m/s.
D) (70,7; 70,7) m/s.
E) (50,7; 60,2) m/s.
Rpta. : "D"
PREGUNTA 26 :
El récord mundial en lanzamiento de bala de 7,3 kg, lo ostenta el estadounidense Randy Barnes, campeón en los Juegos Olímpicos de Atlanta 1996. Su marca fue aproximadamente de 23 m como alcance horizontal máximo. Supongamos que la bala se lanza de tal modo que logre su máximo alcance, determine su rapidez de lanzamiento.
(g = 10m/s²)
A) 12 m/s
B) 15 m/s
C) 18 m/s
D) 15,5 m/s
Rpta. : "B"
PREGUNTA 27 :
Un error frecuente es considerar que en caída libre la trayectoria solo tiene que ser vertical. Sin embargo, en caída libre lo importante es que sobre el proyectil únicamente actúe la gravedad y con ello la trayectoria puede ser parabólica o hasta incluso circunferencial como es el caso de los satélites artificiales. Suponga que una esfera es lanzada horizontalmente del techo de un edificio de altura H, logrando impactar en el suelo luego de 3s con 50m/s. Halle la altura H y su rapidez de lanzamiento , respectivamente.
(g = 10m/s²)
A) 45 m; 40 m/s
B) 30 m; 30 m/s
C) 45 m; 30 m/s
D) 80 m; 40 m/s
E) 60 m; 60 m/s
Rpta. : "A"
PREGUNTA 28 :
De la parte superior de una torre de 5m de altura, se lanza horizontalmente una billa y cae al suelo en un punto situado a una distancia de 5m. Del borde de la torre. Calcule Tgθ donde θ es el ángulo que forma la velocidad de la billa con la horizontal en el instante en que ésta llega al suelo.
(g=10m/s²)
A) 0,5
B) 1/3
C) 2
D) 3
E) 4
Rpta. : "C"
PREGUNTA 29 :
Un joven que esta al nivel del suelo apunta con su escopeta directamente a un coco que cuelga de un árbol. En el instante que sale el disparo, el coco se desprende del árbol y cae. Considerando que el proyectil sale a 75m/s, que el joven esta a 9m de la vertical que pasa por el coco y que éste está a 12m del suelo, determinar la distancia en cm que cae el coco hasta ser impactado por la bala.
(g=10m/s²)
A) 10
B) 15
C) 20
D) 25
E) 30
Rpta. : "C"
PREGUNTA 30 :
Indicar cuales de las siguientes proposiciones son correctas con respecto al movimiento de proyectiles:
I) La altura máxima se produce cuando la velocidad en el eje vertical es máximo.
II) La velocidad en el eje x es constante.
III) La velocidad tiene la misma magnitud para dos instantes t1 y t2 en el que el proyectil se encuentra a la misma altura.
A) Sólo I
B) Sólo II
C) Sólo III
D) I y II
E) II y III
Rpta. : "E"
PREGUNTA 31 :
Una piedra es lanzada con una inclinación de 60° y una velocidad inicial de 40m/s. ¿Al cabo de qué tiempo se encontrará en un plano horizontal que contiene al punto de lanzamiento?
A) 7,61s
B) 6,71s
C) 6,17s
D) 7,06s
E) 6,81s
Rpta. : "D"
PREGUNTA 32 :
Un avión que vuela horizontalmente a razón de 90m/s deja caer una piedra desde una altura de 1000m. ¿Con qué velocidad (aproximada) llega la piedra a tierra si se desprecia el efecto del rozamiento del aire?
A) 140 m/s
B) 166,4 m/s
C) 230 m/s
D) 256,4 m/s
E) 345,6 m/s
Rpta. : "B"
PREGUNTA 33 :
Sobre un techo de un tren, que se mueve en línea recta horizontal y a velocidad constante, está parado un pasajero. El pasajero deja caer una piedra desde lo alto de su mano. ¿Cuál es la trayectoria de la piedra visto por este pasajero? (despreciando la fricción del aire).
A) Horizontal opuesta al movimiento del tren.
B) Vertical hacia abajo.
C) Horizontal en la dirección del movimiento del tren.
D) Describe una curva opuesta al movimiento del tren.
E) Describe una curva hacia el movimiento del tren.
Rpta. : "B"
PREGUNTA 34 :
Un cuerpo cae desde una altura de 19 pies con respecto al piso a una altura de 10 pies, éste choca elásticamente contra un plano inclinado de 30° respecto a la horizontal. Determinar el tiempo que emplea el cuerpo en tocar el piso desde que es soltado
(g=32 pies/s²)
A) 15
B) 2
C) 3
D) 4
E) 0,5
Rpta. : "B"
PREGUNTA 35 :
Un estudiante para medir la altura de un árbol, lanza una pelota desde una distancia horizontal de 42m mediante un aparato desde el suelo con un ángulo de elevación de 53°.Si él constata que el tiempo transcurrido entre el disparo y la llegada de la piedra a la punta del árbol es de 3s. ¿Cuál es la altura (en metros) del árbol?
(Asumir g=10m/s² y tg53°=4/3)
A) 7
B) 9
C) 11
D) 9,6
E) 15
Rpta. : "C"
Cuando uno patea una pelota, ¿qué determina dónde cae?, ¿cómo describimos el movimiento de una bala de cañón o el vuelo de una ave?
No podemos contestar estas preguntas usando las técnicas de capítulos anteriores donde las partículas se movían sólo en línea recta.
Tenemos que aceptar el hecho de que el mundo es tridimensional.
Para entender el vuelo curvo de una pelota de futbol , la órbita de un satélite o la trayectoria de un proyectil, necesitamos extender nuestras descripciones del movimiento a situaciones en 2 y 3 dimensiones.
Seguiremos usando las cantidades vectoriales desplazamiento, velocidad y aceleración pero ahora tendrá dos o tres componentes y no estarán todas en una misma línea.
Veremos que muchos movimientos importantes e interesantes ocurren en sólo 2 dimensiones, es decir, en un plano, y pueden describirse con dos coordenadas y dos componentes de velocidad y aceleración.
Consideramos un movimiento bidimensional durante el cual la aceleración permanece constante. Es decir supóngase que la magnitud y la dirección de la aceleración permanecen invariables durante el movimiento.
El movimiento bidimensional que tiene aceleración constante es equivalente a dos movimientos independientes en las direcciones x y y con aceleración constante ax y ay .
Un proyectil es cualquier cuerpo que recibe una velocidad inicial y luego, sigue una trayectoria determinada totalmente por los efectos de la aceleración gravitacional y la resistencia del aire. Una bola golpeada, un balón lanzado un paquete soltado de un avión y una bala disparada por un rifle son proyectiles. El camino que sigue un proyectil es su trayectoria.
Para analizar este tipo de movimiento, partiremos de un modelo idealizado que representa al proyectil como una partícula y realizamos las siguientes suposiciones:
El alcance es suficientemente pequeño como para despreciar la curvatura de la tierra.
La altura es suficientemente pequeña como para despreciar la variación de la gravedad con la altura.
La partícula tiene una aceleración de la gravedad constante en magnitud y dirección.(1* )
La velocidad inicial tiene un valor suficientemente pequeño como para despreciar la resistencia del aire.( 2* )
Para un proyectil de largo alcance, tal como el mostrado en la figura, donde todos los vectores y señalan hacia el centro de la tierra y varían con la altura. La trayectoria es en este caso, un arco de elipse, como se estudiará más adelante.
La trayectoria de un proyectil de largo alcance no es una parábola, sino un arco de elipse. Si tenemos en cuenta la resistencia del aire, la trayectoria deja de ser parabólica, como se muestra en la figura y el alcance disminuye.
Efecto de la resistencia del aire en el movimiento de un proyectil.
La figura es una simulación por computador de la trayectoria de una pelota con V0 , sin resistencia del aire y con una resistencia proporcional al cuadrado de la rapidez de la pelota.
(1* ) Esta aproximación es razonable siempre que el intervalo de movimiento sea pequeño, comparado con el radio de la tierra (6,4×10⁶m). En efecto, esta aproximación es equivalente a suponer que la tierra es plana a lo largo del intervalo del movimiento considerado.
( 2* ) Por lo general, esta aproximación no se justifica, en especial a altas velocidades.
Además, cualquier giro dado a un proyectil, lo que ocurre cuando un lanzador envía una bola curva, puede dar lugar a ciertos efectos muy interesantes asociados con fuerzas aerodinámicas.
Con estas suposiciones, encontramos que la curva que describe un proyectil (partícula), que llamaremos su trayectoria, siempre es una parábola.
MOVIMIENTO EN EL PLANO CON ACELERACIÓN CONSTANTE
En este movimiento se tiene que la aceleración media es igual a la aceleración instantánea, es decir no interesa el intervalo de tiempo en el cual se determina.
☛ Cada una de las cantidades que intervienen en las diferentes ecuaciones escalares tienen un signo que depende de su orientación con respecto a los ejes coordenados
☛ En general la trayectoria recorrida por el móvil es una parábola.
En el caso particular que la velocidad inicial sea paralela a la aceleración, la trayectoria será una línea recta.
