CAÍDA LIBRE EJERCICIOS RESUELTOS PDF
GUIA DE EJERCICIOS FÁCILES
PREGUNTA 1 :
Un cuerpo se lanza en forma vertical hacia arriba con una rapidez de 800m/s. Calcula el tiempo que demora en subir.
a) 12s
b) 16s
c) 10s
d) 80s
e) 9s
PREGUNTA 2 :
Un cuerpo se lanza verticalmente hacia arriba con una rapidez de 60m/s. Determina el tiempo de vuelo del cuerpo.
a) 18s
b) 16s
c) 14s
d) 12s
e) 10s
PREGUNTA 3 :
Un cuerpo es lanzado hacia arriba demorando en subir 2s. Calcula la rapidez con que se lanzó.
a) 10m/s
b) 20m/s
c) 30m/s
d) 40m/s
e) 60m/s
PREGUNTA 4 :
Un cuerpo es lanzado verticalmente hacia arriba con una rapidez de 30m/s. Calcula el tiempo de subida.
a) 2s
b) 4s
c) 5s
d) 3s
e) 6s
PREGUNTA 5 :
Un cuerpo al ser lanzado hacia arriba demora 5s en bajar. Determina el tiempo que demora en subir.
a) 4s
b) 5s
c) 3s
d) 2s
e) 10s
PREGUNTA 6 :
Un cuerpo se lanza verticalmente hacia arriba con una rapidez de 50m/s. Calcula el tiempo que demora en subir.
a) 8s
b) 7s
c) 6s
d) 5s
e) 4s
PREGUNTA 7 :
Una piedra se lanza desde el piso con una rapidez de 45m/s. Determina el tiempo que demora en regresar a tierra.
a) 4s
b) 9s
c) 8s
d) 4,5s
e) 7s
PREGUNTA 8 :
Un cuerpo se lanza en forma vertical hacia arriba con una rapidez de 40m/s determina el tiempo que demora en alcanzar el punto más alto de su trayectoria.
a) 8s
b) 10s
c) 6s
d) 4s
e) 2s
PREGUNTA 9 :
Un cuerpo demora en bajar 7s. Determina el tiempo que demora en regresar a tierra luego de haber sido lanzado verticalmente hacia arriba.
a) 6s
b) 7s
c) 10s
d) 12s
e) 14s
PREGUNTA 10 :
Un cuerpo se lanza verticalmente hacia arriba con una rapidez de 70m/s. Determina el tiempo de permanencia en el aire.
a) 10s
b) 12s
c) 14s
d) 16s
e) 18s
PREGUNTA 11 :
Un cuerpo se lanza verticalmente hacia arriba con cierta rapidez, si demora en el aire un cuerpo de 12s. Calcula la rapidez con la que fue lanzada.
a) 20m/s
b) 30m/s
c) 40m/s
d) 60m/s
e) 80m/s
PREGUNTA 12 :
Un cuerpo se lanza con una rapidez de 80m/s verticalmente hacia arriba. Determina el tiempo que demora en regresar a la tierra.
a) 10s
b) 12s
c) 14s
d) 16s
e) 18s
PREGUNTA 13 :
Una piedra ha sido lanzada desde el piso con una rapidez de 25m/s. Determina el tiempo que demora en subir.
a) 2,5s
b) 1,5s
c) 5s
d) 3,5s
e) 4,5s
PREGUNTA 14 :
Un cuerpo se lanza verticalmente hacia arriba demorando en bajar 6s. Determina el tiempo de permanencia en el aire.
a) 10s
b) 11s
c) 12s
d) 13s
e) 14s
PREGUNTA 15 :
Un cuerpo alcanza una altura máxima de 320. Determina con qué rapidez fue lanzado el cuerpo desde tierra. (g = 10m/s²)
a) 60m/s
b) 80m/s
c) 90m/s
d) 40m/s
e) 70m/s
PREGUNTA 16 :
Un cuerpo permanece en el aire por espacio de 18s. Calcula la rapidez con que se lanzó verticalmente hacia arriba.
a) 40m/s
b) 50m/s
c) 60m/s
d) 70m/s
e) 90m/s
PREGUNTA 17 :
Si un cuerpo permanece en el aire 10s desde que fue lanzado desde tierra. Halla la altura que alcanza. (g = 10m/s²)
a) 100m
b) 125m
c) 120m
d) 105m
e) 150m
PREGUNTA 18 :
Una piedra se lanza verticalmente hacia arriba con cierta rapidez si el cuerpo permanece en el aire 4s. Calcula la altura máxima.
(g = 10m/s²)
a) 5m
b) 25m
c) 45m
d) 20m
e) 30m
PREGUNTA 19 :
Un móvil es lanzado verticalmente hacia arriba con cierta rapidez si el cuerpo demora en el aire 14s. Calcula su altura máxima.
(g = 10m/s²).
a) 225m
b) 235m
c) 245m
d) 255m
e) 215m
PREGUNTA 20 :
Un cuerpo se lanza hacia arriba con 40m/s. Determina la altura máxima que alcanza el cuerpo. (g =10m/s²)
a) 60m
b) 160m
c) 80m
d) 90m
e) 70m
CLAVES – RESPUESTAS : 1)D 2)D 3)B 4)D 5)B 6)D 7)B 8)D 9)E 10)C 11)D 12)D 13)A 14)C 15)B 16)E 17)B 18)D 19)C 20)C
PROBLEMA 1 :
Se suelta una piedra desde una altura de 320 m. Si g=10m/s2, la distancia que recorre en el último segundo, es:
A) 77 m
B) 79 m
C) 73 m
D) 75 m
E) 71 m
RESOLUCIÓN :
Rpta. : "D"
PRACTICA PROPUESTA I
PREGUNTA 1 :
Un helicóptero que está descendiendo a una velocidad uniforme de 7m/s; deja caer una pelota verticalmente. Calcular la velocidad de la pelota en m/s; al final del primer segundo.
No considere la resistencia del aire. (g=10m/s²)
A) 7 m/s
B) 8 m/s
C)13 m/s
D)17 m/s
E) 15 m/s
Rpta. : "D"
PREGUNTA 2 :
Se lanza una piedra verticalmente hacia arriba desde el fondo de un pozo de 40m de profundidad con una rapidez inicial de 30m/s. ¿Qué tiempo debe transcurrir para que la piedra pase por el borde del pozo?
(g = 10m/s²)
a) 1s
b) 2s
c) 3s
d) 4s
e) 5s
Rpta. : "B"
PREGUNTA 3 :
Un cuerpo cae libremente en el vacío y recorre en el último segundo una distancia de 44,1m. Entonces, el cuerpo cae desde una altura en m de: ... ; (g=9,8 m/s²)
A) 142,5
B) 78,4
C) 122,5
D) 162,5
E) 172,5
Rpta. : "C"
PREGUNTA 4 :
Un objeto cae desde un globo aéreo que baja verticalmente con una rapidez de 15m/s. Determina la altura recorrida por el objeto luego de 10 segundos.
a) 650m
b) 640m
c) 630m
d) 620m
e) 610m
Rpta. : "A"
PREGUNTA 5 :
Un cuerpo cae libremente desde el reposo. La mitad de su caída lo realiza en el último segundo. El tiempo total, en segundos, de la caída es aproximadamente:.......... (g=10m/s²)
A) 3,41
B) 1,21
C) 2
D) 5
E) 8
Rpta. : "A"
PREGUNTA 6 :
Una piedra es lanzada verticalmente hacia arriba desde la azotea de un edificio con una rapidez de 30m/s. Otra piedra se suelta 4s después de lanzar la primera. ¿Qué tiempo se moverá la segunda piedra hasta que la primera logra pasarla?
a) 1s
b) 2s
c) 3s
d) 4s
e) 5s
Rpta. : "E"
PREGUNTA 7 :
Determina la altura de un edificio, sabiendo que un hombre, desde el borde de la azotea lanza una piedra verticalmente hacia arriba a 10m/s, esta llega a tierra luego de 8s.
a) 220m
b) 230m
c) 240m
d) 250m
e) 260m
Rpta. : "D"
PREGUNTA 8 :
Un cuerpo cae libremente y se conoce que recorre entre el momento que toca el piso y el antepenúltimo segundo de caída libre 300m. Halla el tiempo total de caída libre del cuerpo.
(g = m/s²)
a) 12s
b) 13s
c) 14s
d) 15s
e) 16s
Rpta. : "E"
PREGUNTA 9 :
Hallar la altura que alcanza un cuerpo que es lanzado hacia arriba si un segundo después del lanzamiento tiene una rapidez de 40m/s.
(g = 10m/s²)
a) 123m
b) 124m
c) 126m
d) 125m
e) 127m
Rpta. : "D"
PREGUNTA 10 :
Determina la altura máxima de un objeto que al alcanzar la quinta parte de dicha altura posee una rapidez de 20m/s. (g = 10m/s²)
a) 23m
b) 24m
c) 25m
d) 26m
e) 22m
Rpta. : "C"
PREGUNTA 11 :
Desde qué altura “H” se debe dejar caer un cuerpo, para que tarde 10s en recorrer los 13/49H que le falta para llegar al piso. (en metros)
a) 24600m
b) 24500m
c) 24700m
d) 24800m
e) 26800m
Rpta. : "B"
PREGUNTA 12 :
2 cuerpos A y B se encuentran en una línea vertical separados por una distancia de 100 metros, el cuerpo A (esta arriba) se deja caer y simultáneamente el cuerpo B (esta abajo) se lanza hacia arriba con una rapidez inicial de 50m/h. ¿En que tiempo se encontrarán dichos cuerpos? (g = 10m/s²)
a) 2s
b) 3s
c) 4s
d) 5s
e) 1s
Rpta. : "A"
PREGUNTA 13 :
¿Qué altura máxima alcanza un cuerpo lanzado desde tierra, si en el último segundo de ascenso recorre la mitad de la altura máxima? (en pies).
a) 32
b) 42
c) 34
d) 31
e) 41
Rpta. : "A"
PREGUNTA 14 : :
Desde el penúltimo piso de un edificio se deja caer una piedra al mismo tiempo que del último piso se lanza hacia abajo otra piedra con una rapidez inicial de 4m/s, la distancia entre cada piso es de 7m. Calcula al cabo de qué tiempo estarán separados las piedras 3m. Dar el tiempo mínimo (g = 10m/s²)
a) 4s
b) 3s
c) 2s
d) 1s
e) 5s
Rpta. : "D"
PREGUNTA 15 :
Del problema anterior Calcula en que tiempo estarán separados por segunda vez la distancia de 3m las 2 últimas piedras (t máximo)
a) 1,5s
b) 2,5s
c) 3,5s
d) 4,5s
e) 2s
Rpta. : "B"
PREGUNTA 16 :
Se lanzan verticalmente hacia arriba 2 cuerpos con la misma rapidez inicial de 100m/s. Después de cuanto tiempo se encontrarán a la misma altura si una se lanza 4s después de haber lanzado la primera. g = m/s².
a) 15s
b) 14s
c) 13s
d) 12s
e) 9s
Rpta. : "D"
PREGUNTA 17 :
Una piedra se lanza verticalmente hacia arriba desde el techo de un edifico con una rapidez inicial de 30m/s, otra piedra se deja caer 4s después que se ha lanzado la primera. Halla el tiempo en que después de soltar la segunda se encuentran ambas a la misma altura.
g = 10m/s²
a) 2s
b) 4s
c) 6s
d) 8s
e) 5s
Rpta. : "B"
PREGUNTA 18 :
Se lanza verticalmente hacia arriba 2 piedras con intervalo de 1s. la primera tiene una rapidez de 64 pies/s y la otra 112 pies/s. ¿A qué altura sobre el nivel del suelo se encontrarán ambas? (g = 32 píes/s²)
a) 61,44 pies
b) 48 pies
c) 64 pies
d) 46 pies
e) 40 pies
Rpta. : "A"
PREGUNTA 19 :
En cierto planeta se observa que un cuerpo cayendo cerca de la superficie, duplica su velocidad durante un recorrido de 90m en el que tarda 3s.
¿Podría ser este planeta la Tierra?
A) No. La aceleración es muy pequeña.
B) Falta más información para decidir.
C) No. La aceleración es muy grande.
D) Sí, podría ser la Tierra.
E) Se necesitarán cálculos muy complicados para decidir.
Rpta. : "A"
PREGUNTA 20 :
Un globo está ascendiendo y cuando tiene una rapidez de 48 pies/s y se encuentra a una altura de 128 pies, se lanza hacia abajo un lastre con una rapidez de 16 pies/s. ¿En cuánto tiempo el lastre llegará al suelo? (g = 32 pies/s²)
a) 3s
b) 6s
c) 2s
d) 1s
e) 4s
Rpta. : "E"
PREGUNTA 21 :
Lenin lanza una pelota con una velocidad de 15 j (m/s). ¿Cuánto tiempo tarda en regresar a su nivel de lanzamiento?. (g = –10 j m/s²)
a) 3 s
b) 4 s
c) 2 s
d) 1 s
e) 0,5 s
Rpta. : "A"
PREGUNTA 22 :
Un objeto es lanzado con una velocidad de 80 j (m/s). ¿Cuál es su velocidad después de 10 segundos? (g = 10 j m/s²)
a) –22 j (m/s)
b) –20 j (m/s)
c) –18 j (m/s)
d) –15 j (m/s)
e) –12 j (m/s)
Rpta. : "B"
PREGUNTA 23 :
Se lanza un objeto verticalmente hacia arriba con una rapidez inicial de 40 m/s; entonces, su velocidad (módulo y sentido) al cabo de 6 segundos es: (g = 10 m/s²)
a) 20j (m/s)
b) –30j (m/s)
c) 30j (m/s)
d) –20j (m/s)
e) 40j (m/s)
Rpta. : "D"
PRACTICA PROPUESTA II
PROBLEMA 1 :
Desde la azotea de un edificio se lanza verticalmente hacia arriba una esfera y luego de 3 s su rapidez se duplica. Determine la rapidez de lanzamiento. (g= 10 m/s²)
A) 5 m/s
B) 20 m/s
C) 2 m/s
D) 10 m/s
E) 12 m/s
PROBLEMA 2 :
Si luego de lanzar verticalmente hacia arriba una esfera, esta retorna a las manos en 1,20 s, ¿cuánto fue su recorrido total? ( g=10 m/s²)
A) 1,8 m
B) 2,5 m
C) 3,6 m
D) 4,5 m
D) 3,5 m
PROBLEMA 3 :
Una forma sencilla de conocer la altura de un edificio es calcular el tiempo de caída de un cuerpo y con este dato, usar alguna fórmula del MRUV. Si el tiempo de caída de un cuerpo soltado desde la azotea de un edificio fue de 5 s, ¿qué altura tiene el edificio? ( g= 9,8 m/s²)
A) 115,6 m
B) 122,5 m
C) 148,7 m
D) 170,4 m
E) 160,2 m
PROBLEMA 4 :
Una pelota se arroja verticalmente hacia arriba; alcanza su punto más alto y regresa. ¿Cuál de las siguientes afirmaciones es correcta?
A) La aceleración siempre está en la dirección del movimiento.
B) La aceleración siempre se opone a la velocidad.
C) La aceleración siempre está dirigida hacia abajo.
D) La aceleración siempre está dirigida hacia arriba.
E) En una línea horizontal que corte a la trayectoria de la pelota se cumple que la velocidad de subida es igual a la velocidad de bajada de la pelota.
PROBLEMA 5 :
Desde una altura de 100m se deja caer una partícula y al mismo tiempo desde el piso es proyectada otra partícula verticalmente hacia arriba. Si las dos partículas tienen la misma velocidad cuando se encuentran, ¿qué altura ha recorrido la partícula lanzada desde el piso? (g=10m/s²)
A) 60 m
B) 35 m
C) 50 m
D) 20 m
E) 75 m
PROBLEMA 6 :
Considere 2 esferas metálicas A y B. La esfera A se deja caer libremente desde una altura de 30m. En el mismo instante la esfera B, es lanzada hacia abajo desde una altura de 20m con velocidad constante VC en m/s ; para que ambas esferas caigan al suelo al mismo tiempo , VC es: (considere despreciable la resistencia del aire y asuma g=10 m/s²)
A) 10,2
B) 8,16
C) 5,42
D) 4,37
E) 2
PROBLEMA 7 :
En caída libre, todos los cuerpos, independiente de su masa, se mueven con la misma aceleración de la gravedad. Por eso, un martillo y una pluma caerían al mismo tiempo si son soltados desde una misma altura. Si una pluma en caída libre es soltada desde una altura de 2 m, ¿cuántos segundos empleará en recorrer la segunda mitad de su trayectoria?
( g=10 m/s²; √2 = 1,4).
A) 0,08√5
B) 0,01√3
C) 0,02√3
D) 0,03√2
E) 0,03√7
PROBLEMA 8 :
Desde el piso se lanzan pelotas verticalmente hacia arriba, cada 2 segundos, con velocidad de 196m/s. Calcular el número máximo de pelotas, todas en el aire al mismo tiempo que se pueden contar . (g = 9,8 m/s²).
A) 20
B) 15
C) 17
D) 19
E) 21
PROBLEMA 9 :
La aceleración de la gravedad en la Luna tiene un módulo que es la sexta parte de la aceleración de la gravedad en la Tierra. Entonces, si una esfera lanzada en la Tierra verticalmente hacia arriba recorre una máxima altura de 5 m, ¿qué altura máxima alcanzará esta misma esfera lanzada con la misma rapidez pero en la superficie de la Luna?
( g= 9,8 m/s²).
A) 25 m
B) 28 m
C) 30 m
D) 35 m
E) 45 m
PROBLEMA 10 :
En el año 2012, Félix Baumgartner se convirtió en el primer ser humano en lanzarse sin paracaídas desde una altura de 39 000 m y luego de 40 s logró obtener 1173 km/h superando la velocidad del sonido que es de 1130 km/h a esa altura. Hay que precisar, sin embargo, que debido a la fuerza del aire al cabo de un cierto tiempo alcanzó su velocidad límite cayendo a velocidad constante. Entonces si asumiéramos que Félix Baumgartner estuviera en caída libre, ¿cuál sería su velocidad final al cabo de 40 s? ( g= 9,8 m/s²).
A) 1230 km/h
B) 1325,7 km/h
C) 1411,2 km/h
D) 1520,6 km/h
E) 1400 km/h
PROBLEMA 11 :
Una pelota cae verticalmente al piso y rebota en él. La velocidad justo antes del choque es 0,9V. Si la pelota se deja caer desde un metro de altura, a que altura llegará después del primer bote?(g=9,8m/s²)
A) 0,90 m
B) 1,00 m
C) 0,95 m
D) 0,85 m
E) 0,81 m
PROBLEMA 12 :
Un globo se eleva desde la superficie terrestre a una velocidad constante de 5m/s. Cuando se encuentra a una altura de 360m, se deja caer una piedra. El tiempo, en segundos, que tarda la piedra en llegar a la superficie terrestre es:...;
(g=10m/s²).
A) 6s
B) 9s
C) 12s
D) 15s
E) 13s
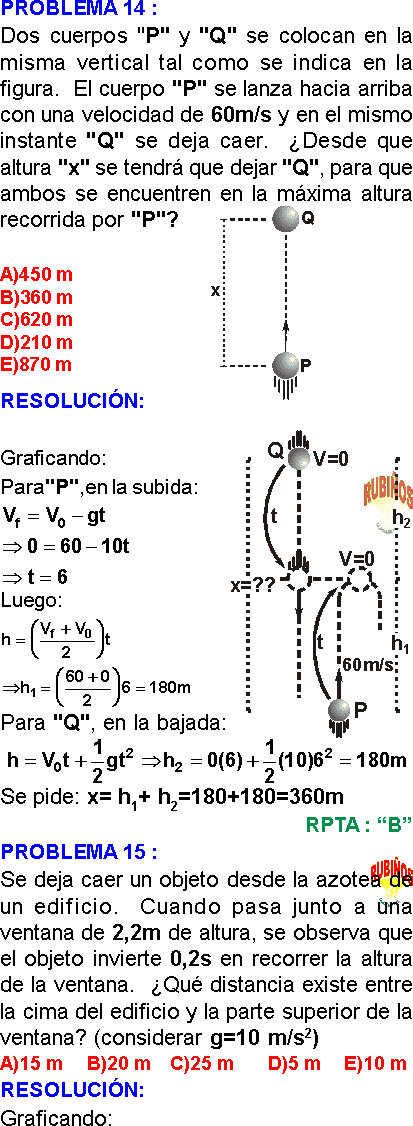
PROBLEMA 13 :
Se deja caer un objeto desde la azotea de un edificio. Cuando pasa junto a una ventana de 2,2m de altura, se observa que el objeto invierte 0,2s en recorrer la altura de la ventana. ¿Qué distancia existe entre la cima del edificio y la parte superior de la ventana? (considerar g=10 m/s²)
A) 15 m
B) 20 m
C) 25 m
D) 5 m
E) 10 m
PROBLEMA 14 :
Un paracaidista después de soltarse de un helicóptero suspendido en el aire cae en forma libre 80m, abre en ese instante su paracaídas disminuyéndole su rapidez a razón de 2m/s por cada segundo. ¿Cuánto tiempo demora su descenso?, si llega al suelo con una rapidez de 2m/s. (g=10m/s²)
A) 21s
B) 23s
C)17s
D) 26s
E) 14s
PROBLEMA 15 :
De la llave de un caño malogrado que está a 7,2m de altura , cae una gota de agua cada 0,1s; cuando está por caer la tercera gota, se termina de malograr el caño y sale un chorro grande de agua. ¿Cuál deberá ser la velocidad con la que sale el chorro para que alcance a la primera gota, en el momento preciso que ésta choca con el piso?
(considerar g=10m/s²)
A) 1,8 m/s
B) 2 m/s
C) 2,2 m/s
D) 2,4 m/s
E) 2,6 m/s
PROBLEMA 16 :
La Torre de Pisa, campanario de la catedral de Pisa, es uno de los íconos más significativos de toda Italia. Es una torre inclinada que mide aproximadamente 57 m, aunque su altura original era de 60 m. Hay una leyenda acerca del experimento que realizó Galileo Galilei en la Torre de Pisa, soltando dos objetos, uno pesado y el otro ligero, para comprobar que ambos caían al mismo tiempo. Considere el experimento realizado por Galileo, ¿luego de cuánto tiempo escuchó el sonido de impacto de la esfera con el piso?
( g=10 m/s²; Vsonido=340 m/s; √3 = 1,73)
A) 2,58 s
B) 2,79 s
C) 3,64 s
D) 4,72 s
E) 4,34 s
PROBLEMA 17 :
Un pasajero, que viaja horizontalmente en un tranvía suficientemente largo observa que un foco se desprende del techo del tranvía y llega al piso en 2s. Determinar la altura del tranvía, si en el momento de la caída del foco, disponía de una aceleración constante. (g=10m/s²)
A) 10 m
B) 20 m
C) 5 m
D)15 m
E) 40 m
PROBLEMA 18 :
Lenin con una pelota en la mano, está parado sobre una plataforma que sube con una aceleración constante de 3m/s². Si lenin lanza la pelota, verticalmente hacia arriba con una velocidad de 39m/s ¿qué tiempo debe esperar Lenin para volver a tener la pelota en sus manos? (g =10m/s²)
A) 3s
B) 6s
C) 9s
D) 12s
E) 13s
PROBLEMA 19 :
Un globo se eleva verticalmente con una velocidad constante de 10m/s, cuando este se encuentra a 15m del piso , se abandona un lastre ¿con qué velocidad y luego de cuántos segundos caerá el lastre al piso? ¿qué distancia separará en ese instante al globo? (g=10m/s²)
A) 10m/s; 5s y 28m
B) 8m/s; 2s y 4m
C) 17m/s; 5s y 60m
D) 9m/s; 5s y 62m
E) 20m/s; 3s y 45m
PROBLEMA 20 :
Indique las proposición(es) correcta(s) respecto de la caída libre de los cuerpos:
I) El valor de la aceleración de la gravedad es diferente en el Ecuador que en los polos.
II) Deben actuar otras fuerzas aparte del peso.
III) La aceleración de caída libre depende del volumen de los cuerpos.
A) Sólo I
B) Sólo II
C) Sólo III
D) Sólo I y III
E) Sólo I y II
PROBLEMA 21 :
Dentro de un ascensor que baja con una aceleración constante de 4m/s², se encuentra un niño con una moneda entre manos, la moneda es lanzada verticalmente hacia arriba con una velocidad de 2m/s. ¿Después de qué tiempo, la moneda tocará el piso del ascensor, si las manos del niño dista 1m del piso del ascensor.
A) 2s
B) 1s
C) 3s
D)1,5 s
E) 0,7s
CLAVES – RESPUESTAS : 1)D 2)C 3)B 4)C 5)E 6)B 7)A 8)A 9)C 10)C 11)E 12)B 13)D 14)B 15)C 16)C 17)B 18)B 19)E 20)A 21)B
MOVIMIENTO VERTICAL DE CAÍDA LIBRE–MVCL
¿Qué es el movimiento de caída libre?
El movimiento vertical de caída libre o MVCL es aquel de trayectoria recta y vertical donde su aceleración es constante, por ello es un caso particular del M.R.U.V.
Un cuerpo está en caída libre cuando solo influye la atracción de la gravedad.
Entonces usaremos sus mismas ecuaciones del MRUV, de modo que se cambia a=g.
¿Cuáles son las características de un movimiento de caída libre ?
Sus principales características son:
☛ Se desprecia la resistencia del aire y no influye la masa del cuerpo
☛ La trayectoria es rectilínea, vertical (dirigida hacia el centro de la tierra)
☛ Durante el movimiento la aceleración de la gravedad permanece constante
☛ Para alturas pequeñas con respecto al radio terrestre, el movimiento vertical cumple con las leyes del movimiento rectilíneo uniformemente variado. (MRUV)
APRENDIZAJES ESPERADOS :
☛ Reconocer las características de un movimiento de caída Libre.
☛ Describir el movimiento vertical de caída libre “MVCL” .
☛ Emplear las fórmulas del MRUV en la solución de problemas del MVCL.
☛ Describir las propiedades del movimiento vertical de caída libre en el análisis del movimiento.
☛ Utilizar las ecuaciones escalares y vectoriales del MVCL para determinar las variables cinemáticas.
☛ Aplicar los números de Galileo en los problemas donde se pida calcular recorridos, alturas y tiempos.
¿Cuándo los cuerpos están en caída libre?
Si despreciamos la resistencia del aire, es decir los cuerpos sólo son afectados por la atracción terrestre, entonces diremos que los cuerpos se encuentran en caída libre.
Galileo planteo que en ausencia del aire (vacío) la piedra y la pluma descienden en línea recta tal que para iguales desplazamientos se emplean tiempos iguales.
¿Qué es la gravedad ?
En las cercanías de la superficie terrestre los cuerpos al caer experimentan la misma aceleración, esta aceleración se conoce como la aceleración de la gravedad “g” la cual es constante y su valor es: g=9,8m/s²
Para fines prácticos g=10m/s²
¿Qué nos indica el valor g=10m/s²?
La aceleración nos indica que por cada 1s que transcurre la rapidez del cuerpo cambia en 10m/s.
¿POR QUÉ CAEN LOS CUERPOS?
La causa por la cual todos los cuerpos caen es por el hecho de que ellos se ven atraídos por la Tierra.
La intensidad de esta atracción es conocida con el nombre de peso, y éste es mayor en los cuerpos que poseen mayor masa; así, una piedra tiene más peso que una pluma, porque la masa de la piedra es mayor.
¿CUANDO UN CUERPO ESTA EN CAIDA LIBRE?
Se dice que un cuerpo está en caída libre cuando al moverse sólo se ve afectado de su propio peso. Esto ocurrirá únicamente en el vacío.
Si soltamos un cuerpo cerca de la superficie terrestre, éste caerá libremente, describiendo una trayectoria recta y vertical; si lanzamos oblicuamente un cuerpo, éste se encontrará en caída libre, pero describiendo una trayectoria parabólica.
Y si lanzamos un satélite al espacio vacío y alrededor de la Tierra, diremos que también está en caída libre, pero describiendo una trayectoria circunferencial.
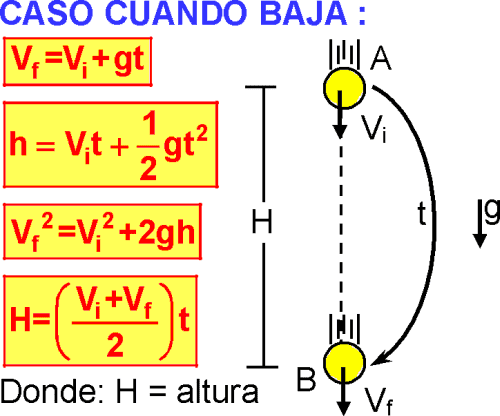
ECUACIONES ESCALARES DE LA CAÍDA LIBRE
Como el MVCL es un caso particular del MRÜV, en el cual ambos presentan trayectoria rectilínea y aceleración constante, se usarán las mismas ecuaciones del MRUV para el cálculo donde a=g y d=h.
ECUACIONES VECTORIALES DE LA CAÍDA LIBRE
Muchas veces cuando tenemos un cuerpo que asciende y luego desciende verticalmente, primero analizamos el ascenso y luego el descenso, resultando algunas veces muy tedioso, por lo que podemos abreviar el análisis del movimiento a través del uso de las ecuaciones vectoriales, las cuales se muestran a continuación.
¿Cuáles son las propiedades de un movimiento vertical de caída libre ?
Si despreciamos la resistencia del aire (en el vacío), todos los cuerpos caen simultáneamente, independientemente de su forma y masa (postulado establecido por Galileo respecto a la caída libre de los cuerpos). .
• Las trayectorias que describen los móviles son líneas rectas y verticales.
• A medida que descienden, la velocidad cambia; es decir, hay una aceleración, la cual es constante y recibe el nombre de aceleración de la gravedad
• En cada segundo de movimiento, el valor de la velocidad varía en una cantidad igual al valor de la aceleración.
• Si un cuerpo es lanzado verticalmente hacia arriba, el valor de su velocidad disminuye en 9,8 m/s en cada segundo.
• Para un mismo nivel horizontal, la rapidez de ascenso (subida) y de descenso (bajada) son iguales.
• Cuando un cuerpo es lanzado verticalmente hacia arriba y alcanza su altura máxima, en este instante su velocidad es cero, pero su aceleración es diferente de cero.
• En un MVCL, los tiempos de subida y de bajada son iguales para un mismo nivel en cualquier instante.
• Si un cuerpo se suelta desde cierta altura, en el primer segundo su recorrido es igual a la mitad del valor de la aceleración. En los siguientes segundos, el recorrido aumenta en el valor de la aceleración.
• Si un cuerpo es lanzado verticalmente hacia arriba, su recorrido en cada segundo disminuye en el valor de la aceleración, y en el último segundo de su ascenso, su recorrido es igual a la mitad del valor de la aceleración.
ATRACCIÓN TERRESTRE
La causa por la cual todos los cuerpos caen es por el hecho de que ellos se ven atraídos por la tierra.
La intensidad de esta atracción se denomina "peso", y éste es mayor en los cuerpos que poseen mayor masa.
ACELERACIÓN DE LA GRAVEDAD (g) :
Soltando una piedra sabemos que parte del reposo y que su rapidez va en aumento mientras cae.
La piedra acelera mientras cae debido a la atracción terrestre.
La aceleración que adquieren los cuerpos a causa de la atracción terrestre se llama aceleración de la gravedad (g).
La aceleración de la gravedad (g) tiene las siguientes características.
VARIACIÓN DE LA GRAVEDAD
La aceleración de la gravedad no es la misma en todos los lugares de la tierra; depende de la latitud y de la altura sobre el nivel del mar. "g" tiene un valor diferente en cada lugar de la Tierra. Cada cuerpo celeste tiene su propio valor para su aceleración de la gravedad.
Debe tener en cuenta que el cuerpo en caída libre experimenta una aceleración especial, la cual es conocida como "aceleración de la gravedad" y su valor, para nuestros problemas, será cerca de la Tierra , de 9,8 m/s². para facilidad de los problemas, a veces se toma el valor de la aceleración de la gravedad como 10m/s², pero es necesario que el problema lo especifique.
