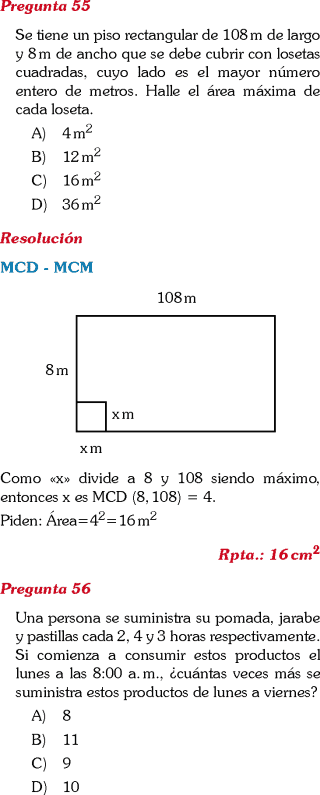
SIMULACRO CATÓLICA 2025 RESUELTO CLAVES INGRESO UNIVERSIDAD

PREGUNTA 1 :

La diferencia de dos números es 20; la diferencia de sus cuadrados también es 20. Encuentre la razón geométrica de menor a mayor, de dichos números.

A) 19

B) 9

C) 19/21

D) 17/19

Rpta. : "C"

PREGUNTA 2 :

Encuentre el M.C.D. de 32 ; 24 ; 72.

A) 6

B) 12

C) 8

D) 24

Rpta. : "C"

PREGUNTA 3 :

La piscina de un hotel tiene la capacidad de 2 000 000 litros. Si el costo del metro cúbico de agua es de 35 céntimos. ¿Cuánto cuesta llenar la piscina, en soles?

Nota: 1m³=1000L

A) 350

B) 7000

C) 700

D) 70

Rpta. : "C"

PREGUNTA 4 :

Una persona compra papa y maíz a S/.1 y S/.2, respectivamente, el kilo; si en total compra una tonelada y no gasta menos de S/.1200, ¿cuántos kilos de papa, como máximo, compró?

A) 900

B) 800

C) 700

D) 1000

Rpta. : "B"

PREGUNTA 5 :

En una progresión geométrica los tres primeros términos son x;x+1;x+5. Indique el 5to término.

A) 27

B) 81/4

C) 72/25

D) 27/8

Rpta. : "B"

PREGUNTA 6 :

Un número tiene como únicos factores primos a 2 y 3. La cantidad de divisores de la raíz cuadrada de dicho número es 12, y la cantidad de divisores de su cuadrado es 117. ¿Cuántos divisores tiene dicho número?

A) 24

B) 36

C) 35

D) 28

Rpta. : "C"

PREGUNTA 7 :

¿Cuántos números de cuatro cifras distintas se pueden escribir utilizando únicamente los dígitos: {0;1;2;3;4;5;6}?

A) 288

B) 360

C) 640

D) 720

Rpta. : "D"

PREGUNTA 8 :

Al tostar café se pierde el 20% del peso. Si se vende a S/ 9,2 el kilo de café tostado, ganando el 15 % del precio de costo del café, calcule el costo por kilo de café adquirido.

A) S/ 8,0

B) S/ 6,4

C) S/ 7,08

D) S/ 6,81

Rpta. : "B"

PREGUNTA 9 :

Un granjero tiene una vaca y una cabra. Si el peso de la vaca excede los 100 kg a los 2/3 del peso de la cabra; y que el peso de la cabra excede en 20 kg de la doceava parte del peso de la vaca. Calcule la suma de los pesos de la vaca y la cabra.

A) 160

B) 140

C) 150

D) 200

Rpta. : "C"

PREGUNTA 10 :

De las siguientes expresiones:

I. El máximo Común Divisor (M.C.D.) de 2 o más números, es el menor número que los divide exactamente.

II. El valor del M.C.D. de varios números es igual al producto de los factores primos comunes y no comunes elevados a sus menores exponentes.

III. Si se dividen varios números entre su M.C.D. Los cocientes son primos entre sí.

IV. Un conjunto de números de números tiene un M.C.D. igual a "D". Si cada uno de ellos se multiplica por una constante "n", entonces el M.C.D. de los números es igual a "n" veces "D". ¿Cuántas son falsas?

A) 4

B) 2

C) 3

D) 1

Rpta. : "B"

CLIC AQUÍ Ver SOLUCIONARIO DE NÚMEROS Y OPERACIONES PUCP

ESTADÍSTICA

PREGUNTA 11 :

Julia debe responder 8 de las 10 preguntas de un examen. ¿De cuántas formas puede elegir las 8 preguntas que responderá?

A) 90

B) 45

C) 60

D) 75

Rpta. : "B"

PREGUNTA 12 :

De un grupo de 15 alumnos, a 9 les gusta la matemática, a 4 solo letras y los que gustan de matemática y letras son tantos como los que no gustan de estos cursos. ¿Cuántos gustan de ambos?

A) 1

B) 3

C) 4

D) 2

Rpta. : "D"

PREGUNTA 13 :

En el siguiente cuadro se muestran las ganancias en millones de soles de 3 empresas de transporte en sus rutas: norte, centro y sur.

Calcule la ganancia de la empresa B en su ruta sur, en millones de soles.

A) 12

B) 14

C) 16

D) 18

Rpta. : "A"

PREGUNTA 14 :

El promedio de las edades de 50 personas es "x". Si a cada una de las edades de las personas se le aumenta 40 años, el nuevo promedio es "y". Indique la clave correcta.

A) x + 10 = y

B) 2x + y = 50

C) x – 10 = y

D) x + y = 50

Rpta. : "A"

PREGUNTA 15 :

Tres hombres y 4 mujeres van al cine y encuentran 7 asientos disponibles. ¿De cuántas maneras se pueden sentar, si las mujeres ocupan los lugares impares y María se quiere sentar en un extremo?

A) 24

B) 48

C) 72

D) 96

Rpta. : "C"

PREGUNTA 16 :

Con la información de la tabla, calcule el promedio del valor del producto en nuevos soles.

A) 38

B) 50,8

C) 60,5

D) 61,6

Rpta. : "C"

PREGUNTA 17 :

Se arrojan 2 monedas, una de 50 céntimos y otra de 1 sol. Calcule la probabilidad del evento: "Que salga por lo menos una cara". Entendiendo como "cara" al lado de la moneda que muestra la denominación.

A) 1/4

B) 3/4

C) 1/2

D) 1

Rpta. : "B"

PREGUNTA 18 :

Calcule el número de elementos del conjunto:

A={x∈ℕ/x+1 es impar, x<27/4}

A) 2

B) 3

C) 4

D) 5

Rpta. : "C"

PREGUNTA 19 :

En una urna se encuentran mezcladas 8 bolas azules, 8 bolas rojas, 5 negras y 5 verdes. Se extraen 3 bolas al azar una por una sin reposición. ¿Cuál es la probabilidad de que la primera bola extraída sea roja y las siguientes sean iguales pero no rojas?

A) 20/1950

B) 56/1950

C) 76/1950

D) 96/1950

Rpta. : "D"

PREGUNTA 20 :

En una bolsa hay 32 caramelos de piña, fresa y limón, las probabilidades de dichas cantidades son 0,25 ; 0,625 y 0,125 respectivamente. ¿Cuántos caramelos más de fresa que de piña hay?

A) 8

B) 12

C) 4

D) 10

Rpta. : "B"

CLIC AQUÍ Ver SOLUCIONARIO DE ESTADÍSTICA PUCP

ÁLGEBRA

PREGUNTA 21 :

Las edades de tres hermanos son 15 ; 17 y 33 años. ¿Dentro de cuántos años la edad del mayor será igual a la suma de los otros dos hermanos?

A) 4

B) 3

C) 2

D) 1

Rpta. : "D"

PREGUNTA 22 :

Factorice:

P(a;b)=4–a²–b²+2ab

A) (2 – a – b)(2 + a + b)

B) (2 + a – b)(2 – a + b)

C) (a + b + 2)(a + b – 2)

D) (4 + a – b)(4 – a + b)

Rpta. : "B"

PREGUNTA 23 :

Se sabe que la ecuación cuadrática x²–9x+b=0 tiene como raíz al número 2. Calcule la otra raíz.

A) 1

B) 5

C) 7

D) 11

Rpta. : "C"

PREGUNTA 24 :

Calcule el valor de:

A) 10

B) 12

C) 13

D) 15

Rpta. : "D"

PREGUNTA 25 :

Reduzca la expresión:

A) 2ⁿ

B) n

C) 2

Rpta. : "C"

PREGUNTA 26 :

Forme la ecuación cuadrática en “x” de raíces 5/3 y 3/10 .

A) 30x²+59x–15 = 0

B) 30x²–59x+15 = 0

C) 30x²+59x+15 = 0

D) 30x²–59x–15 = 0

Rpta. : "B"

PREGUNTA 27 :

Dada la función cuadrática f(x)=x²+2bx–5 con b>0. Calcule el valor de "b" si se sabe que f(b)=22.

A) 1

B) 2

C) 3

D) 5

Rpta. : "C"

PREGUNTA 28 :

Calcule el residuo de la división:

A) 8 – 9x

B) 9x – 8

C) 8x + 9

D) 9 – 8x

Rpta. : "D"

PREGUNTA 29 :

Dadas las siguientes rectas:

ℒ₁: y–x–2=0 ∧ ℒ₂: y–2x–m=0, calcule la variación de "m" para que las rectas se intersecten en un punto ubicado en el segundo cuadrante.

A) 〈1;5〉

B) 〈2;4〉

C) 〈3;5〉

D) 〈4;6〉

Rpta. : "B"

PREGUNTA 30 :

Resuelva la siguiente ecuación:

Rpta. : "D"

CLIC AQUÍ Ver SOLUCIONARIO DE ÁLGEBRA PUCP

GEOMETRÍA

PREGUNTA 31 :

Se tiene un rectángulo de perímetro igual a 30m y área igual a 36m². Calcule la diferencia de sus lados.

A) 10 m

B) 9 m

C) 6 m

D) 8 m

PREGUNTA 32 :

Se tiene un triángulo rectángulo cuyos lados están en progresión aritmética. Calcule la medida del menor ángulo de dicho triángulo.

A) 37°

B) 53°

C) 30°

D) 60°

PREGUNTA 33 :

En el gráfico, BC=10, DC=DE=4. Calcule el área del trapecio ABCE.

A) 36 u²

B) 50 u²

C) 70 u²

D) 56 u²

PREGUNTA 34 :

En un triángulo ABC, las longitudes de los lados AB y BC están en relación de 1 a 3. Se traza la bisectriz interior BD, si AD=1, calcule DC.

A) 1

B) 2

C) 3

D) 4

PREGUNTA 35 :

De gráfico calcule m∢ABCD, si AD=2CBC.

A) 80°

B) 60°

C) 30°

D) 90°

PREGUNTA 36 :

Del gráfico, calcule el área de la región sombreada (P, T, Q: Puntos de tangencia).

PREGUNTA 37 :

Se tiene un cubo cuya diagonal de una cara es 12. Calcule el área total de dicho cubo.

A) 400 u²

B) 200 u²

C) 432 u²

D) 462 u²

PREGUNTA 38 :

En el gráfico, calcule O₁O₂, si R=13u y r=10u.

PREGUNTA 39 :

Se tiene un tronco de cono de altura igual a 8m y radios de sus bases igual a 4m y 6m lleno de agua, y un cilindro de radio 20m y altura 57m. Calcule cuántos troncos de cono se necesitarán para llenar al cilindro.

A) 110

B) 110,5

C) 100

D) 112,5

PREGUNTA 40 :

Del gráfico calcule: DC – AD

A) 6

B) 7

C) 4

D) 5

CLIC AQUÍ Ver SOLUCIONARIO DE GEOMETRÍA PUCP

TRIGONOMETRÍA

PREGUNTA 51 :

Del gráfico, calcule el valor de tanθ, si senθ=3/5

A) 3/2

B) 2/3

C) 3/4

D) 5/6

Rpta. : "B"

PREGUNTA 52 :

Convierta 9°/𝛑 al sistema radial.

Rpta. : "D"

PREGUNTA 53 :

Reduzca la expresión:

A) 1

B) 2

C) 3

D) 4

Rpta. : "A"

PREGUNTA 54 :

Sabiendo que (4x+11) grados sexagesimales equivale a 3𝛑/20 radianes. Determine el valor de x.

A) 2

B) 3

C) 4

D) 5

Rpta. : "C"

PREGUNTA 55 :

Calcule el valor de:

A) 3

B) – 3

C) √2

D) –√2

Rpta. : "B"

PREGUNTA 56 :

Determine los cuadrantes donde es positiva la expresión:

A) IC ∨ IIC

B) IC ∨ IIIC

C) IIIC ∨ IIC

D) IIC ∨ IVC

Rpta. : "D"

PREGUNTA 57 :

La suma de las medidas de dos ángulos es 5𝛑/4 radianes y el mayor ángulo excede al menor en 75°. Calcule el suplemento del mayor ángulo en radianes.

A) 𝛑/3 rad

B) 𝛑/4 rad

C) 𝛑/6 rad

D) 𝛑/2 rad

Rpta. : "C"

PREGUNTA 58 :

Si a un sector circular, se le duplica su radio sin alterar el valor de su área. Calcule la relación de las medidas de los ángulos centrales.

A) 1

B) 1/2

C) 1/3

D) 4

Rpta. : "D"

PREGUNTA 59 :

Sea un triángulo ABC, como en el gráfico.

A) 4

B) 3

C) 2

D) 1

Rpta. : "A"

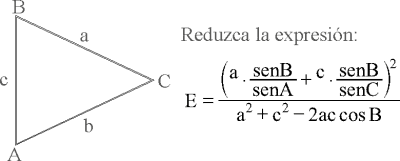
PREGUNTA 60 :

Reduzca la expresión:

Rpta. : "C"

CLIC AQUÍ Ver SOLUCIONARIO DE TRIGONOMETRÍA PUCP

LECTURA

TEXTO 1

Uno de los pilares sobre el que el sistema feudal sustentaba su ideología era el consenso. Este se basaba en la persuasión, la capacidad de convicción por parte del poder de que la realidad social respondía al orden natural de las cosas y a la voluntad divina. Dicho orden dividía a la población en tres estamentos. El primero, el pueblo llano, mayoritariamente campesino y siervo, formaba la amplia base de la pirámide social: obedecía, trabajaba, pagaba impuestos o efectuaba prestaciones. El segundo era la nobleza poseedora de las tierras, los feudos, que, a cambio de los tributos y del trabajo que recibía de sus siervos, los socorría y protegía de asaltantes e invasores. El tercero, la Iglesia, muchas veces también dueña de feudos, rezaba por las almas de todos los fieles y justificaba la conservación del orden social, mientras poseía y administraba, casi en exclusividad, la cultura y el conocimiento.

En la cúspide de la pirámide, se hallaba el rey, un noble al que todos los demás nobles debían vasallaje y quien también ejercía jurisdicción directa sobre determinadas tierras o ciudades, como cualquier otro noble. Estas relaciones conformaban lo que los historiadores han llamado pacto o contrato feudal, que tenía, no solo una naturaleza económica, sino también política. Cada estamento cumplía su papel social: el pueblo trabajaba, el clero rezaba y los nobles combatían. Iglesia y nobleza se apoyaban entre sí, legitimándose mutuamente en sus funciones y, de esta manera, promovían el consenso favorable al mantenimiento del orden social.

PREGUNTA 61 :

¿Qué es cierto sobre el rol de la nobleza en el sistema feudal según el texto?

A) La nobleza era poseedora de tierras y feudos, lo que le daba un poder absoluto.

B) Los nobles se dedicaban a combatir y, de esa forma, protegían al pueblo y al clero.

C) Los nobles eran vasallos del rey y cobraban tributo a los siervos a cambio de protegerlos.

D) La nobleza le pagaba tributo al rey y protegía a sus vasallos de los posibles invasores.

Rpta. : "C"

PREGUNTA 62 :

¿Cuál es la intención principal del texto?

A) Informar sobre el estancamiento de las clases sociales

B) Informar sobre la sociedad feudal

C) Describir la organización del sistema feudal

D) Criticar el orden del sistema feudal

Rpta. : "C"

TEXTO 2

La historia y la reflexión sobre la participación de las mujeres en política es larga; sin embargo, conviene iniciarla con algunas interrogantes: ¿por qué tendrían las mujeres que contar con paridad en los poderes políticos?, ¿las mujeres necesitan a mujeres para que las representen? Algunas autoras como Ann Phillips e Iris M. Young piensan que lo que se dice se puede separar de quien lo dice. Pese a ello, también se considera que la paridad significaría un cambio en la política: la creciente presencia de mujeres traería cambios sustanciales en las instituciones, las prioridades y en la cultura política. En este texto, definimos las cuotas de género, más conocidas como cuotas de participación por sexo o cuotas de participación de mujeres, como una forma de acción, cuyo objetivo es garantizar la efectiva integración de mujeres en cargos electivos de decisión de los partidos políticos y del Estado. Es una medida de carácter compulsivo, que exige incorporar mujeres en listas de candidaturas o en listas de resultados electorales, y transitorio, puesto que supone una vigencia sujeta a la superación de los obstáculos que impiden una adecuada representación de mujeres en los espacios de poder y representación política. Asimismo, es importante tener en cuenta que la idea central de los sistemas de cuotas es seleccionar mujeres para puestos en las instituciones de gobierno y garantizar que estas no queden marginadas de la vida política o tengan una presencia meramente decorativa [...] Hoy en día, los sistemas de cuotas buscan asegurar que las mujeres constituyan al menos una “minoría decisiva” del 30 al 40 %.

Hay toda una polémica a favor y en contra de esta medida discriminatoria, correctora de una escasez, temporal y justificada en cada contexto social y en nuestros días. Si bien es cierto que se trata de discriminación en positivo, es discriminación al fin y al cabo, y el debate se centra en la justicia, equidad y carácter democrático de dicha medida. De esta manera, pese a que existen una serie de argumentos a favor de esta idea (evitar la discriminación y fomentar la igualdad de oportunidades entre hombres y mujeres, permitir la presencia de las mujeres en la vida pública, visibilizar la discriminación de género y mantener el tema en la agenda política del país, y ampliar y profundizar la democracia misma), los argumentos en contra son más contundentes. Entre estos, tenemos, primero, la cuestionable idoneidad de los sujetos discriminados, ya que puede haber otros grupos en situación similar, políticamente subrepresentados, y puede tener lugar incluso una discriminación hacia los mismos. Segundo, va en contra del principio de la igualdad de oportunidades y resulta, por tanto, discriminatorio e, incluso, antidemocrático. Tercero, se minusvaloran los méritos, capacidades y preparación de las personas. Cuarto, se soslaya la libre competencia entre contendientes, y de elección por parte de los partidos y de la ciudadanía. Por último, puede tratarse de una mera medida de imagen o de “lo políticamente correcto”.

PREGUNTA 63 :

El hecho de que el autor coloque los argumentos a favor de las cuotas de género en política le sirven para

A) ilustrar que estos son falsos.

B) justificar que la cuota de género es antidemocrática.

C) demostrar que los argumentos en contra son más determinantes.

D) describir detalladamente la postura contraria.

Rpta. : "C"

PREGUNTA 64 :

¿Cuál es el significado más adecuado para el término “compulsivo” (subrayado en el texto)?

A) Psicótico

B) Obligatorio

C) Democrático