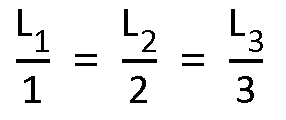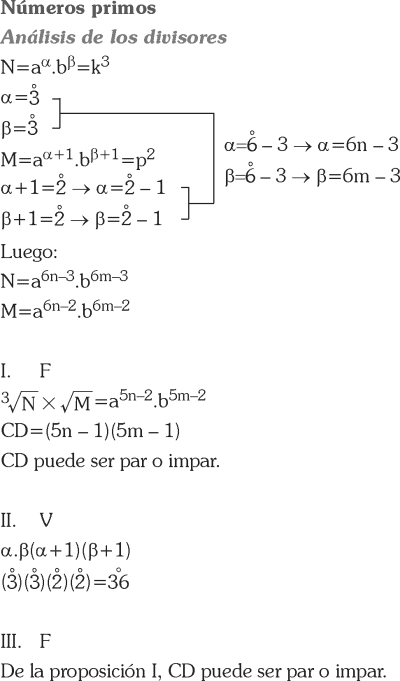UNI 2024-1 SEGUNDA PRUEBA CLAVES DE INGRESO UNIVERSIDAD DE INGENIERÍA SOLUCIONES DE MATEMÁTICA PDF
CLAVES – RESPUESTAS :
1)A 2)C 3)B 4)E 5)C 6)A 7)C 8)A 9)D 10)A 11)E 12)D 13)C 14)A 15)E 16)E 17)D 18)E 19)B 20)A 21)A 22)E 23)D 24)C 25)C 26)B 27)B 28)A 29)A 30)D 31)A 32)A 33)A 34)D 35)C 36)A 37)A 38)C 39)D 40)A
PREGUNTA 1 :
La suma de las cifras de los cuatro últimos dígitos de
A) 11
B) 13
C) 16
D) 17
E) 19
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 2 :
Se dispone de tres recipientes cúbicos cuyos lados de longitud L1, L2, L3 cumplen con la siguiente condición:
Se pretende distribuir 434 litros de agua entre los tres recipientes de modo que alcancen el mismo nivel o altura. Determine los litros de agua que recibe el recipiente de longitud L2.
A) 112
B) 120
C) 124
D) 136
E) 146
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 3 :
Se elige aleatoriamente un número entero de cinco cifras. Calcule la probabilidad que dicho número sea par y la suma de sus cifras sea 42.
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 4 :
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 5 :
Sea r el residuo de dividir
Determine cuáles de las siguientes proposiciones son verdaderas.
I) r=6, si n es par
II) r=6, si n es impar
III) r=2, si n es impar
A) solo I
B) solo II
C) solo III
D) I y II
E) I y III
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 6 :
Sea la fracción a/3 (a y 3 primos entre sí), con a > 0.
Al numerador le agregamos el número A∈ℕ y al denominador 2A, se obtiene una fracción equivalente que es la mitad de la fracción original, entonces la suma de todos los valores posibles de a es:
A) 4
B) 8
C) 9
D) 12
E) 15
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 7 :
Indique la alternativa correcta después de determinar si la proposición es verdadera (V) o falsa (F), según el orden dado:
I) Entre dos números racionales existe al menos un número irracional.
II) El número 𝛑 se puede expresar exactamente como un número racional r=22/7 .
III) La suma de dos números irracionales es un número irracional.
A) VVV
B) VVF
C) VFF
D) FVF
E) FFF
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 8 :
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 9 :
Sean a; b; c∈ℝ tales que 0<a<b <c y x1<x2. Siendo (x1;y1) y (x2;y2) soluciones del sistema de ecuaciones
y=ax2+bx+c
y=cx2+bx+a
entonces podemos afirmar que
A) x1, x2, y1, y2>0
B) x1, x2 <0; y1, y2>0
C) x1, x2 >0; y1, y2<0
D) x1<0; x2, y1, y2>0
E) x1 >0; y1, y2<0
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 10 :
Determine los puntos de intersección de la gráfica de la función definida por
f (x)=|x − 2|+x2 con la recta 3x–2y=–11
A) ( – 1; 2), (3; 9)
B) (1; – 4), (3; 10)
C) (–1; 4), (3; 10)
D) ( – 1; 1), (4; 9)
E) (1; – 4), (3; 12)
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 11 :
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 12 :
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 13 :
Considere la progresión aritmética
donde la suma de los tres primeros términos es mayor que 170. Si n es el menor posible, calcule la suma de los primeros 12 términos de esta progresión.
A) 1150
B) 1330
C) 1340
D) 1350
E) 1650
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 14 :
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 15 :
Sean las ecuaciones
y=x2–3x+4
y=mx+3
Determine los valores reales de m para que nunca se intersequen.
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 16 :
Si E=〈–∞;2] es el conjunto solución de la inecuación |x – a| ≤ |x – b| , 0<a<b, entonces el menor valor de (a+b)2 es:
A) 8
B) 10
C) 12
D) 14
E) 16
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 17 :
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 18 :
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 19 :
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 20 :
Al efectuar la división
el término independiente del cociente que resulta es
A) – 2n
B) – n
C) 0
D) n
E) 2n
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 21 :
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 22 :
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 23 :
En el ángulo triedro trirectángulo O - ABC; si las áreas de las caras OAB, OBC y OAC miden
respectivamente 𝕊, 2𝕊 y 3𝕊. Entonces el área de la región que determina un plano secante a las aristas y que pasa A, B y C es
A) 2S√2
B) 3S√2
C) S√14
D) 2S√3
E) S√15
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 24 :
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 25 :
La superficie lateral de un prisma recto regular triangular es un rectángulo cuya diagonal mide 12m y su altura 6√3m. Calcule el área total del sólido (en m2).
A) 38√3
B) 39√3
C) 40√3
D) 41√3
E) 42√3
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 26 :
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 27 :
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 28 :
Determine la longitud (en cm) del lado de un polígono regular inscrito en una circunferencia C de radio R cm si la longitud del lado de un polígono de doble número de lados inscrito en C es igual a R/2 cm.
A) √15R/2
B) √15R/3
C) √15R/4
D) √15R/5
E) √15R/6
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 29 :
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 30 :
La figura representa un cubo de arista a cm. Calcule el área (en cm²) de la circunferencia que pasa por los puntos P, Q, R, S, T, U; teniendo en cuenta que son puntos medios de las aristas.
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 31 :
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 32 :
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 33 :
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 34 :
RESOLUCIÓN :
PREGUNTA 35 :
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 36 :
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 37 :
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 38 :
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 39 :
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 40 :
Dada la ecuación general de la cónica : Ax2+By2+Cx+Dy+F=0 con A, B, C, D, F constantes arbitrarias, se tiene que:
I) Si A=B ≠ 0, entonces siempre tenemos la ecuación de una circunferencia.
II) Si B=0 y A ≠ 0, entonces siempre tenemos la ecuación de una parábola.
III) Si A.B<0 y D2– 4BF<0, entonces siempre tenemos la ecuación de una hipérbola.
Luego son verdaderas:
A) solo I
B) II y III
C) solo II
D) solo III
E) I y III
RESOLUCIÓN :
Rpta. : "D"
EJERCICIO 1 :