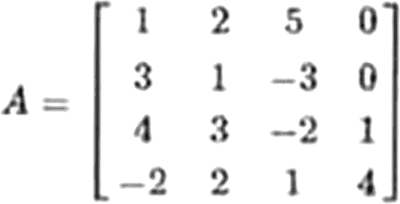UNI 2022 II SEGUNDA PRUEBA SOLUCIONARIO ADMISIÓN UNIVERSIDAD INGENIERÍA MATEMÁTICAS 2022-2 PDF
PREGUNTA 1 :
La fracción 1/17 como una expresión decimal de base 3 se puede escribir como:
A) 0,0021123...(3)
B) 0,0011202...(3)
C) 0,0183294...(3)
D) 0,0121234...(3)
E) 0,0021212...(3)
PREGUNTA 2 :
Se tiene una mezcla de agua con azúcar de concentración 0,75 gramos/litro que al agregar agua se obtiene un volumen de 1 litro de concentración 0,55 gramos/litro.
Halle la cantidad de agua que se agregó en litros.
A) 3/15
B) 1/15
C) 5/15
D) 2/15
E) 4/15
PREGUNTA 3 :
¿Cuántos números de 4 cifras de la base 7 son cuadrados perfectos?
A) 29
B) 33
C) 31
D) 30
E) 32
PREGUNTA 4 :
Calcule el menor valor de a + b + c sabiendo
es un cuadrado perfecto.
A) 9
B) 10
C) 7
D) 11
E) 17
PREGUNTA 5 :
Halle la cantidad de múltiplos de 30 que tiene la siguiente sucesión
24; 48; 72; 96; ...; 24 000 y dé como respuesta la suma de las cifras de dicha cantidad.
A) 9
B) 11
C) 10
D) 8
E) 12
PREGUNTA 6 :
¿Cuántas cifras, como mínimo, puede tener el número a3b4c–3 , si a, b, c tienen 4; 3; 4 cifras respectivamente?
A) 7
B) 5
C) 6
D) 4
E) 8
PREGUNTA 7 :
En un salón de clase de una localidad, los estudiantes son de una ciudad A o de una ciudad B.
Hombres Mujeres
Ciudad A 18 2
Ciudad B 70 10
Sea:
x = la probabilidad de que al escoger al azar un estudiantes, este sea mujer dado que es de la ciudad A.
y = la probabilidad de que al escoger al azar un estudiante, este sea hombre dado que es de la ciudad B.
Halle x+y.
A) 0,910
B) 0,875
C) 0,975
D) 0,925
E) 0,850
PREGUNTA 8 :
Usando interés simple, un capital de 12 000 soles en 2 años genera un interés de 600 soles, un capital de 6000 soles genera en 4 años un interés I.
Dé como respuesta la suma de las cifras de I.
A) 6
B) 3
C) 2
D) 4
E) 5
PREGUNTA 9 :
Sean a y b números enteros positivos tales que a<b
MCD(a; b) = 36
MCM(a; b) = 504
Indique, ¿cuántos pares (a; b) cumplen con estas condiciones?
A) 5
B) 3
C) 2
D) 4
E) 1
PREGUNTA 10 :
Las temperaturas medias en grados centígrados registradas en una ciudad durante el mes de junio fueron:
Halle la temperatura promedio en grados centígrados en el mes de junio.
A) 16
B) 15
C) 17
D) 14
E) 13
PREGUNTA 11 :
Luego de resolver la ecuación
A) 1
B) 3
C) 0
D) 2
E) Más de 3
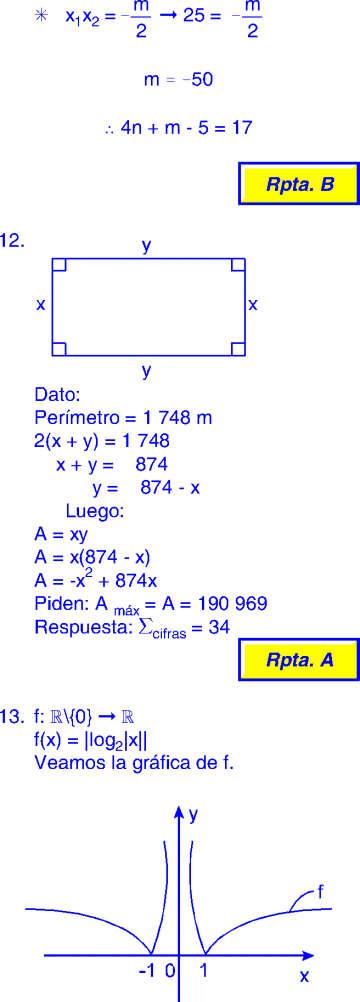
PREGUNTA 12 :
De la siguiente igualdad
(3x² – 5x+ 8)(x+ 8) = (3x+ 4)(x²+ 16) +ax(bx – c)
el valor de la suma de las cifras de (ac – ab) es:
A) 12
B) 10
C) 8
D) 9
E) 11
PREGUNTA 13 :
Sean m, n enteros,
(−x8 + 2√mx4 − 4m)m (x5 −m5 )m (x +n)n+1≤0
donde el conjunto solución es
〈– ∞; – 4] ∪ [5; + ∞〉.
Halle 2m+n.
A) –14
B) –13
C) –6
D) 3
E) 14
PREGUNTA 14 :
Dado el problema de programación lineal:
minimizar U(x; y) =x+y
sujeto a
6x+3y≥1200
2x+3y≥600
x≥0
y≥0
Entonces, el valor mínimo del problema dado es
A) 150
B) 350
C) 250
D) 300
E) 200
PREGUNTA 15 :
La suma de
A) 13/3
B) 11/3
C) 19/3
D) 8/3
E) 17/3
PREGUNTA 16 :
Dada la siguiente matriz:
Halle ∛det(A).
A) 0
B) – 3
C) – 2
D) 3
E) 2
PREGUNTA 17 :
Sea la función objetivo R(x; y) =5x+8y y el siguiente conjunto factible
Calcule el valor máximo de R.
A) 24
B) 20
C) 21
D) 22
E) 23
PREGUNTA 18 :
Sea f: ℝ → ℝ con regla de correspondencia
f(x) = – ax²+bx+ c con a>0
Halle el valor máximo que toma la función f.
A) (b² + 4ac)÷(4b)
B) (b² + 2ac)÷(4a)
C) (b² + 4ac)÷(2a)
D) (b² + ac)÷(4a)
E) (b² + 4ac)÷(4a)
PREGUNTA 19 :
Dado el siguiente sistema de ecuaciones lineales:
2x+3y – 5z =33
– 3x+y+2z = – 11
x+2y+4z = – 8
Halle el valor de x+y+z.
A) – 1
B) 0
C) – 2
D) 2
E) 1
PREGUNTA 20 :
En una tienda hay 63 personas y se tiene la siguiente información:
☛ 7 mujeres tienen 27 años.
☛ 18 mujeres no tienen 27 años.
☛ 16 mujeres no tienen 28 años.
☛ 11 hombres no tienen 27 ni 28 años.
¿Cuántos hombres tienen 27 o 28 años?
A) 32
B) 25
C) 31
D) 30
E) 27
PREGUNTA 21 :
Determine el punto de intersección que se encuentra más alejado del origen entre la recta
ℒ : x – 2y+4=0
y la parábola
ℙ : x² – 2y – 2= 0.
Dé como respuesta la suma de coordenadas.
A) 1
B) 13/2
C) –1
D) 15/2
E) − 11/2
PREGUNTA 22 :
Una empresa compra una computadora en 4000 dólares, después de cuatro años el valor de la computadora se espera que sea de 200 dólares. Si V es el valor de la computadora en el tiempo t (en años), entonces use la ecuación lineal que relaciona V y t para determinar el valor de V en dólares cuando t = 2.
A) 2150
B) 2200
C) 2000
D) 2050
E) 2100
PREGUNTA 23 :
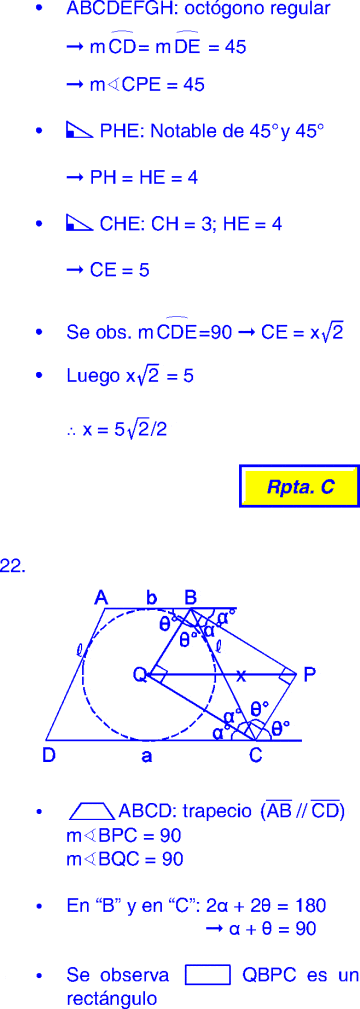
Determine el rango de la siguiente función:
PREGUNTA 24 :
Si x≥ 1, indique el valor de
A) 0
B) 1
C) 3
D) 2
E) 4
PREGUNTA 25 :
Si tan(x) = 3, calcule el valor de
M=13sen(3x) – 9cos(3x) +5
A) 8
B) 4
C) 7
D) 6
E) 5
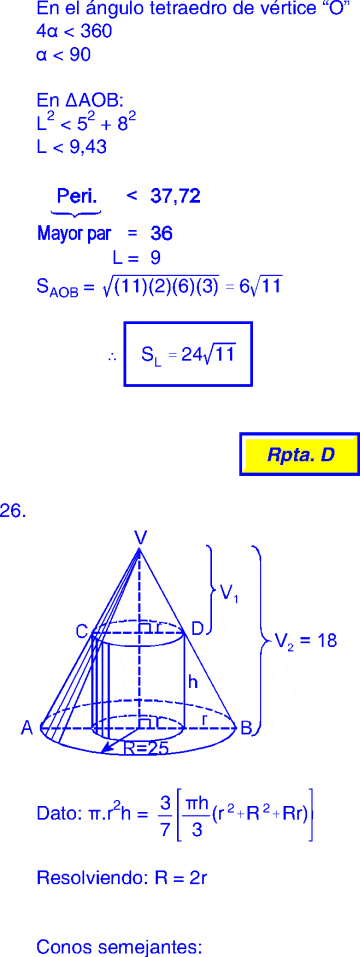
PREGUNTA 26 :
Determine el conjunto solución de la siguiente ecuación trigonométrica:
PREGUNTA 27 :
Sean S y C números reales que representan las medidas en grados sexagesimales y centesimales, respectivamente, para un mismo ángulo tal que
La medida del ángulo en radianes es:
A) 𝛑/30
B) 𝛑/60
C) 𝛑/50
D) 𝛑/20
E) 𝛑/40
PREGUNTA 28 :
En un triángulo ABC se cumple que m∢ACB= 60°, además
A) 5√3
B) 6√3
C) 2√3
D) 3√3
E) 4√3
PREGUNTA 29 :
Indique la alternativa correcta, después de determinar si la proposición es verdadera (V) o falsa (F) en cada uno de los siguientes enunciados.
I) sen160°< sen70°< sen50°
II) sen1<sen2<sen3
III) tan(sen2)>tan(sen1) > tan(sen3)
A) FVV
B) VVV
C) FFV
D) FFF
E) FVF
PREGUNTA 30 :
En la figura adjunta:
Si M y N trisecan al segmento AB, entonces el valor de
√13senθ+ √5senθ es:
A) 4
B) 2
C) 5
D) 3
E) 6
PREGUNTA 31 :
Un tetraedro regular se proyecta sobre un plano perpendicular a una arista. Si la longitud de la arista del tetraedro es 8, determine el área de dicha proyección.
A) 16√2
B) 8√2
C) 12√2
D) 16√3
E) 9√2
PREGUNTA 32 :
Se desea diseñar un molde como se muestra en la figura siguiente:
Sobre el diámetro de un semicírculo de centro O, se toman segmentos AB, BO, OD y DE de igual longitud, los cuales son diámetros de las semicircunferencias F, G, H e I. Si el diámetro del semicírculo mayor es 2R entonces la medida de la longitud total de dichas semicircunferencias menores es
A) 2𝛑R
B) 𝛑R/2
C) 𝛑R2
D) 𝛑R
E) 3𝛑R/4
PREGUNTA 33 :
Dada una pirámide de base cuadrada, se traza un plano paralelo a la base consiguiéndose así una pirámide menor tal que su base cortante tiene área de 6 unidades cuadradas. Si la relación de alturas entre las pirámides es de 1 a 3 y el lado de la base de la pirámide mayor es el doble de su altura, determine el volumen de la pirámide menor.
A) 5√6/3
B) 8 √6/3
C) 2√6/3
D) √6
E) 4√6/3
PREGUNTA 34 :
Un hacendado compra un terreno en forma de hexágono regular de área total 18√3 m². Luego se cerca el terreno que se encuentra dentro del polígono que se obtiene al unir los puntos medios de los lados consecutivos del terreno original. Una vez cercado el terreno, contrata a un pintor para pintar la parte exterior del cerco que tiene 2 m de altura. Sabiendo que 1 galón de pintura alcanza para 4 m², determine la cantidad de galones que se necesitan para pintar lo solicitado por el hacendado.
A) 3√3
B) 18
C) 9
D) 15
E) 18√3
PREGUNTA 35 :
Determine el volumen (en cm³) de un tronco de prisma recto cuyas bases son un triángulo equilátero FED y un triángulo rectángulo isósceles ABC. Además, una cara lateral es un rectángulo de lados 6√2 cm y 12 cm, tal que las aristas laterales son mayores que las aristas de las bases.
A) 224
B) 242
C) 262
D) 252
E) 432
PREGUNTA 36 :
Los puntos F, M, A y G son colineales y consecutivos.
Si
FG= 27
FM=x – y
MA=x+y
AG=2y – x
Calcular el menor valor de x sabiendo que el valor de y es entero.
A) 11
B) 9
C) 27
D) 1
E) 13
PREGUNTA 37 :
Se ubican los puntos A y B, uno a cada lado de un plano 𝛑, de modo que la distancia de estos hacia el plano están en la relación de 1 a 3, respectivamente. Si la proyección del segmento AB sobre el plano mide 24 unidades y el ángulo que forma AB con el plano 𝛑 es de 53°, determine AB (en unidades).
A) 40
B) 30
C) 20
D) 15
E) 60
PREGUNTA 38 :
De la figura mostrada:
se tiene que BD es bisectriz del ángulo ABE y BE es bisectriz del ángulo ABC.
Si x+y+z = 70, determine el valor de xy+z
A) 204
B) 100
C) 202
D) 200
E) 102
PREGUNTA 39 :
El desarrollo de la superficie lateral de un cono de revolución es un sector circular de radio 10 cm y un ángulo central de medida 216°.
Determine el volumen del cono original (en cm³).
A) 92𝛑
B) 96𝛑
C) 76𝛑
D) 128𝛑
E) 81𝛑
PREGUNTA 40 :
Los lados de un triángulo ABC inscrito en una circunferencia miden:
AB=12, AC=10 y BC=8
Por B se traza una recta tangente a la circunferencia que corta a la prolongación del lado AC en M.
Redondee el valor de BM.
A) 27
B) 12
C) 14
D) 10
E) 9
CLAVES-RESPUESTAS : 1)B 2)E 3)D 4)D 5)* 6)C 7)C 8)A 9)C 10)D 11)C 12)E 13)E 14)C 15)A 16)D 17)A 18)E 19)E 20)E 21)B 22)E 23)D 24)B 25)E 26)D 27)A 28)B 29)C 30)A 31)A 32)D 33)D 34)C 35)D 36)A 37)A 38)C 39)B 40)B
