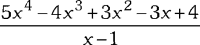TEOREMA DEL RESTO EJERCICIOS RESUELTOS PDF
TEOREMA DEL RESIDUO O DE DESCARTES
El objetivo es hallar el resto de una división sin efectuarla; este teorema se aplica por lo general cuando el divisor es de la forma , o también para cualquier expresión transformable a dicha forma.
PROCEDIMIENTO PARA APLICAR EL TEOREMA DEL RESTO
𝑖) El divisor se iguala a cero (x – m=0) Se iguala el divisor a 0 . Si el divisor es de primer grado, se despeja ‘‘x’’. Si el divisor es de grado mayor que 1, se despeja una expresión adecuada (por lo general, la mayor potencia de ‘‘x’’.
𝑖𝑖) Se despeja la variable (x=m) Se acomoda el dividendo, formando en él la expresión despejada anteriormente. Si el divisor es de primer grado, no es necesario realizar esto.
𝑖𝑖𝑖) Se reemplaza en el dividendo (P(m)) obteniéndose el resto.
Es decir se reemplaza el valor de ‘‘x’’ (si el divisor es de primer grado) o el valor de aquella expresión (si el divisor es de grado mayor que 1), en aquel dividendo.
Luego de efectuar las operaciones correspondientes, el resultado que se obtiene es el resto.
PROBLEMA 1 :
Halla el resto al dividir:
A) 3
B) 4
C) 5
D) 6
E) 2
RESOLUCIÓN :
Usaremos el teorema del resto.
x–1= 0 ⇒ x=1
Reemplazamos en el dividendo.
R= 5(1)4– 4(1)3 + 3(1)2 – 3(1) +4
⇒ R=5
Rpta. : "C"
PROBLEMA 2 :
Hallar el valor de «k» para que el polinomio: u³+v³+w³+kuvw sea divisible entre: u+v+w
A) 1
B) 0
C) –10
D) –2
E) –3
RESOLUCIÓN :
Utilizando el criterio del teorema del resto:
u+v+w=0 ⇒ u³+v³+w³=3uvw
(identidad condicional)
Reemplazando en la expresión propuesta:
3uvw+kuvw=0 (por ser divisible) ; de donde: 3uvw=–3uvw ⇒ k=–3
Rpta. : "E"
PROBLEMA 3 :
Cuál debe ser el valor de r para que el polinomio: 2x³+2x²y–xy+r sea divisible por: x+y
A) y
B) – y
C) 2y
D) y3
E) –y²
RESOLUCIÓN :
Por el teorema del resto:
x+y=0 ⇒ x=–y
Reemplazando en el polinomio:
2(–y)³ – 2(–y)²y– (–y)y+r=0...(por ser divisible)
De donde:
–2y³+2y³+y²+r =0 ⇒ r=–y²
Rpta. : "E"
PROBLEMA 4 :
Sea 2x³+ 10x²– 14x – 3 , ¿cuánto hay que aumentarle al coeficiente de x² para que la división entre (x–3) sea exacta?.
A) 11
B) 12
C) –10
D) –11
E) 12
Rpta. : "D"
PROBLEMA 5 :
El cociente de dividir un polinomio de tercer grado entre 2x–1es: x²+2x–3 y el resto al dividir dicho polinomio entre 2x+1 es 1.
Averigüe el resto que se obtiene al dividirlo entre 2x–1.
A) – 6,5
B) –15
C) 4,5
D) 3,5
E) 2,5
Rpta. : "A"
PROBLEMA 6 :
Un polinomio P(x) se ha dividido por 2x+1 y x–1 hallándose los residuos 6 y 3 respectivamente, entonces el resto de la división P(x)÷(2x+1)(x–1) es:
Rpta. : "–2x+5"