FÍSICA PRE SAN MARCOS SEMANA 1 SOLUCIONARIO SOLUCIONARIO PROBLEMAS RESUELTOS PDF
MAGNITUDES FÍSICAS
☛ su caracterización y representación matemática
VECTORES Y ESCALARES
☛ Análisis dimensional
☛ Adición y sustracción de vectores: métodos geométricos
ANÁLISIS DIMENSIONAL Y ADICIÓN DE VECTORES
FÍSICA: CIENCIA FUNDAMENTAL
La física se ocupa de la comprensión y descripción de los fenómenos naturales mediante principios físicos que son concordantes con las observaciones experimentales.
Un principio físico es una proposición que indica una propiedad general de un fenómeno natural. Se expresa con exactitud en la forma de una ecuación matemática llamada ecuación de la física. Las ecuaciones de la física constituyen la receta para diseñar instrumentos de medida que permitan la comprobación experimental del principio físico.
LA MEDICIÓN EN LA FÍSICA
La medición es una técnica mediante la cual asignamos un número a una propiedad física como resultado de compararla con otra similar tomada como unidad patrón.
A cada propiedad física medible se le asigna un nombre, llamado en general cantidad física.
En general, cuando se tiene una propiedad física medible se cumple la correspondencia:
EL SISTEMA INTERNACIONAL DE UNIDADES (SI)
Las mediciones se expresan en unidades convencionales. A un conjunto de unidades estándar se les llama sistema de unidades. En la actualidad, el sistema de unidades predominante en el mundo es el sistema métrico. La nueva versión del sistema métrico (MKS) se denomina Sistema Internacional de Unidades (SI).
Una cantidad física se considera fundamental cuando se define, de modo independiente, a partir de una propiedad física considerada universal. Por el contrario, se llama cantidad física derivada cuando se define en términos de una o más cantidades físicas fundamentales.
ANÁLISIS DIMENSIONAL
Es el procedimiento que permite comprobar si una ecuación de la física es dimensionalmente homogénea.
ECUACIÓN DIMENSIONAL
Es el resultado de examinar la homogeneidad de una ecuación. Indica las dimensiones fundamentales de un sistema de unidades.
PRINCIPIO DE HOMOGENEIDAD DIMENSIONAL
Establece una condición para que una ecuación sea dimensionalmente homogénea: Todos los términos de una ecuación de la física tienen la misma dimensión.
CLASIFICACIÓN DE LAS CANTIDADES FÍSICAS
CANTIDADES ESCALARES
Se describen indicando solamente su magnitud.
Por ejemplo, la temperatura de un cuerpo se describe con solo leer el número en la escala del termómetro.
Otros ejemplos de escalares son masa, presión, densidad, etc.
CANTIDADES VECTORIALES
Se describen indicando su magnitud, dirección y sentido. Por ejemplo, la velocidad de un cuerpo se describe, analíticamente, indicando la rapidez con que se mueve el cuerpo y su dirección. Otros ejemplos de vectores son fuerza, aceleración, desplazamiento, etc.
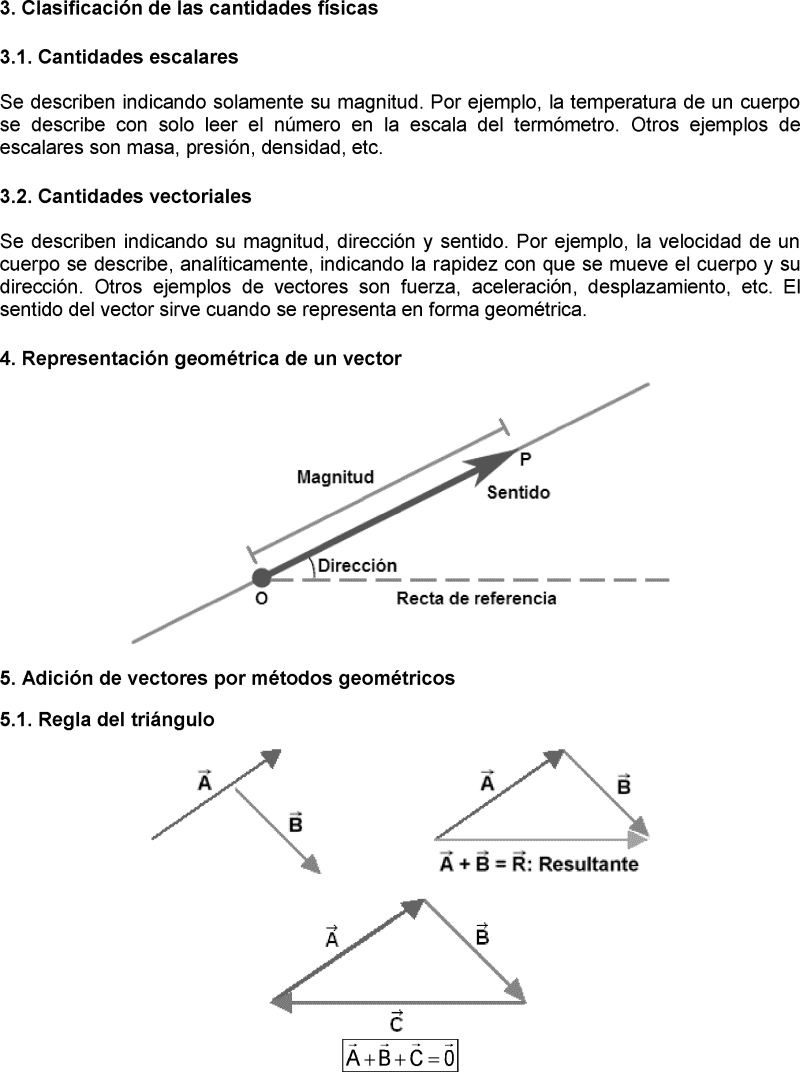
El sentido del vector sirve cuando se representa en forma geométrica.
TRASLACIÓN DE VECTORES
Los vectores graficados se pueden trasladar a cualquier lugar siempre que se conserven sus tres elementos: magnitud, dirección y sentido. En caso contrario, el vector que se traslada ya no es el mismo y, por consiguiente, la operación no es válida.
PREGUNTA 1 :
Un automóvil se desplaza en una trayectoria rectilínea de acuerdo con la ecuación dimensionalmente homogénea: v = a + bt + ct² , donde v : velocidad y t : tiempo.
Utilizando el análisis dimensional, indique la verdad (V) o falsedad (F) de las siguientes proposiciones:
I. La dimensión de a es LT−¹
II. La dimensión de b es LT−²
III. La dimensión de c es LT−³
A) VVF
B) VVV
C) FVF
D) FVV
PREGUNTA 2 :
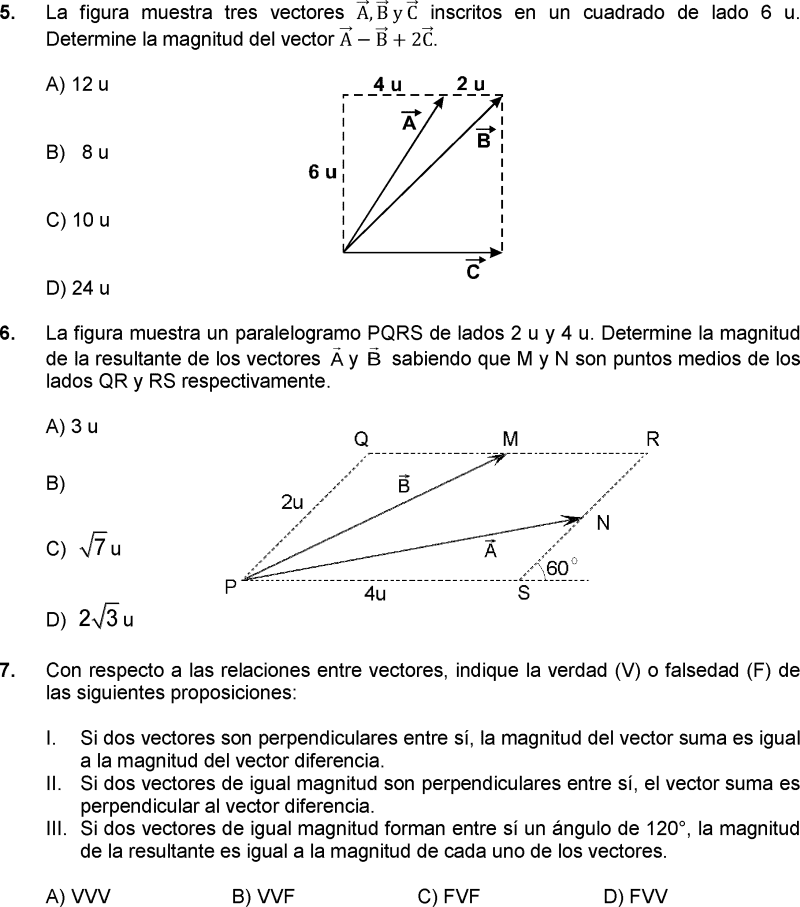
Con respecto a las relaciones entre vectores, indique la verdad (V) o falsedad (F) de las siguientes proposiciones:
I. Si dos vectores son perpendiculares entre sí, la magnitud del vector suma es igual a la magnitud del vector diferencia.
II. Si dos vectores de igual magnitud son perpendiculares entre sí, el vector suma es perpendicular al vector diferencia.
III. Si dos vectores de igual magnitud forman entre sí un ángulo de 120°, la magnitud de la resultante es igual a la magnitud de cada uno de los vectores.
A) VVV
B) VVF
C) FVF
D) FVV
*