PROBABILIDADES EJEMPLOS Y EJERCICIOS RESUELTOS PDF
PRACTICA
PREGUNTA 1 :
Al lanzar dos dados normales , ¿cuál es la suma que mayor probabilidad de ocurrencia tiene?
A) 12
B) 7
C) 13
D) 5
E) 6
PREGUNTA 2 :
Al lanzar una moneda 3 veces consecutivas, ¿cuál es la probabilidad de obtener tres sellos?
A) 1/2
B) 1/4
C) 1/8
D) 1/32
E) 1/5
PREGUNTA 3 :
En una urna se tiene fichas numeradas consecutivamente desde 1 hasta 20 . ¿Cuál es la probabilidad de que al extraer una ficha se obtenga un múltiplo de 3?
A) 0,1
B) 0,3
C) 0,7
D) 0,8
E) 0,5
PREGUNTA 4 :
Se lanzan 2 dados simultáneamente ¿Calcular cuántos elementos tiene el espacio muestral?.
A) 6
B) 12
C) 24
D) 36
E) 216
PREGUNTA 5 :
Determinar la probabilidad de que el resultado sea 7, al lanzar 2 dados?
A)7/36
B)1/6
C)3/5
D) 4/5
E) 9/17
PREGUNTA 6 :
Al lanzar 2 dados . ¿Cuál es la probabilidad de que el resultado de los 2 dados no sea 7?
A)1/6
B)2/7
C)5/6
D) 7/36
E) 29/36
PREGUNTA 7 :
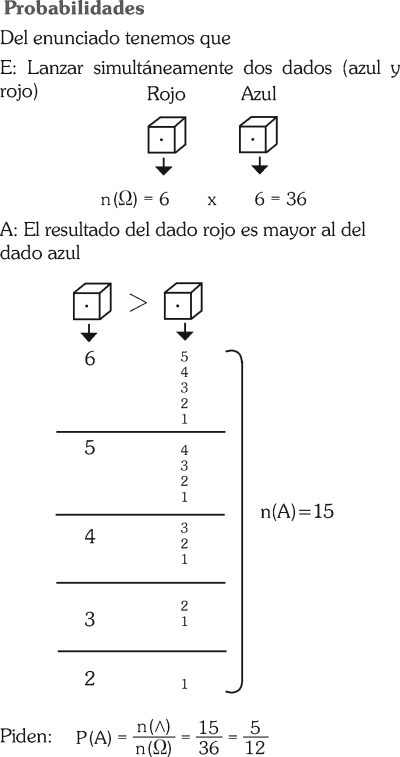
Al lanzar 2 dados , ¿Cuál es la probabilidad de que el resultado del primer dado sea mayor que el segundo?.
A)1/6
B)1/2
C)1/3
D) 1/30
E) 5/12
PREGUNTA 8 :
Determinar la probabilidad de que al extraer 2 cartas de una baraja , éstas sean corazones .
A)1/13
B)1/2
C)1/17
D) 3/28
E)4/27
PREGUNTA 9 :
En una caja hay 10 bolas numeradas del 1 al 10. Se extrae al azar una bola. ¿Cuál es la probabilidad que el número de la bola extraída no exceda de 10?
A) 0,25
B) 0,5
C) 1
D) 1/3
E) 2/11
PREGUNTA 10 :
Se quiere seleccionar un comité de 5 personas a partir de 7 mujeres y 6 varones ¿Qué probabilidad habría que el Comité esté integrado por 2 mujeres?
A)1/7
B)37/91
C)141/429
D)140/429
E)3/38
PREGUNTA 11 :
Se va ha seleccionar por lote un comité de 5 hombres, a partir de un grupo de 8 norteamericanos, 5 ingleses y 3 franceses. ¿Cuál es la probabilidad de que el comité esté compuesto por 2 norteamericanos , 2 ingleses y 1 francés?
A)3/5
B)7/13
C)5/26
D) 1/9
E)31/63
PREGUNTA 12 :
Si se lanza 5 veces un dado ¿cuál es la probabilidad de que las 5 caras que aparecen sean diferentes?.
A)7/23
B)31/32
C)1/32
D) 1/3
E) 5/54
PREGUNTA 13 :
De una baraja de 52 cartas, se sacan 3 naipes de uno en uno , y se devuelven después de cada extracción . ¿Cuál es la probabilidad de que todos sean tréboles?
A)1/4
B)1/13
C)1/16
D)1/64
E)1/21
PREGUNTA 14 :
Un artillero dispara a un blanco. Si la probabilidad de acertar un disparo es 0,01 ¿qué probabilidad tiene de no acertar?
A) 0,72
B) 0,81
C) 0,92
D) 0,7
E) 0,99
PREGUNTA 15 :
Sabiendo que la probabilidad de que ocurra un accidente en 1 km de una carrera es 1/3 ¿Cuál es la probabilidad de que ocurra encontrar al menos un accidente en 3 km de esa carretera?
A)1/3
B)1/27
C)8/27
D)2/3
E)19/27
PREGUNTA 16 :
Las probabilidades que tienen A , B y C de resolver un mismo problema son 1/2 ; 3/5 y 1/6 : respectivamente. Si intentan hacerlo los tres , determinar la probabilidad de que se resuelva el problema.
A)1/3
B)5/6
C)1/2
D) 1/6
E) 1/5
PREGUNTA 17 :
Si se arrojan 5 monedas, ¿Cuál es la probabilidad de obtener 3 sellos y 2 caras?
A) 0,5
B) 0,32
C) 0,3275
D) 0,1
E) 0,3125
PREGUNTA 18 :
A una señora embarazada le diagnosticaron que tendría cuatrillizos . ¿Cuál es la probabilidad que el día del parto nazcan 4 mujeres?
A)1/8
B)1/2
C)1/16
D)1/24
E)1/6
PREGUNTA 19 :
En una competencia atlética de 100 m intervienen, los atletas A , B , C , D y E. ¿Cuál es la probabilidad de que al finalizar B llegue luego de A ?.
A)1/12
B)1/3
C)1/4
D) 1/5
E) 3/4
PREGUNTA 20 :
En un concurso participan 7 alumnos y 8 alumnas, si deben haber 2 ganadores, ¿cuál es la probabilidad de que los ganadores sean una pareja mixta?
A) 8/17
B) 5/11
C) 7/13
D) 8/15
E) 4/9
PREGUNTA 21 :
En una caja hay 10 focos de los cuales 4 están en buen estado, una persona toma al azar 3 focos . Hallar la probabilidad de que por lo menos uno esté en buen estado.
A) 2/3
B) 1/12
C) 5/6
D) 1/6
E) 1/5
PREGUNTA 22 :
Considere un dado “trucado’, de tal forma que la probabilidad de que salga cierto número es inversamente proporcional al mismo. ¿Cuál es la probabilidad de que al lanzar 2 dados trucados idénticos, la suma de los números obtenidos sea 5?
A) 0,14
B) 0,24
C) 0,28
D) 0,34
E) 0,39
PREGUNTA 23 :
Hallar la probabilidad de que al lanzar tres dados , la suma de los números que se obtengan sea igual a 10 .
A)1/2
B) 0,25
C) 0,125
D) 0,75
E) 0,7
CLAVES – RESPUESTAS : 1)B 2)C 3)B 4)D 5)B 6)C 7)E 8)C 9)C 10)D 11)C 12)E 13)D 14)E 15)E 16)B 17)E 18)C 19)D 20)D 21)C 22)A 23)C
PROBLEMAS RESUELTOS
PREGUNTA 1 :
Si se lanza simultáneamente dos monedas; una de un sol y la otra de cincuenta céntimos, ¿cuál es la probabilidad de obtener al menos una cara?
A) 3/8
B) 1/4
C) 1/2
D) 1
E) 3/4
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 2 :
En un sorteo, el primer premio es de S/. 2 000 y el segundo premio es de S/. 1 000. Si se vendieron 100 boletos y Pepito compró 5 boletos, ¿cuál es la probabilidad de ganar S/. 3 000?
A) 1/125
B) 1/300
C) 1/100
D) 5/100
E) 1/495
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 3 :
Un juego consiste en lanzar dos dados. Si la suma de los puntajes es mayor que 10 o menor que 3, se gana un punto; en caso contrario se da un castigo.
Determina:
I. La probabilidad de ganar un punto.
II. La probabilidad de obtener un castigo.
III. La probabilidad de que la suma de los puntajes sea 7.
A) 1/8 ; 7/8 ; 1/6
B) 2/9; 7/9 ; 1/12
C) 1/9 ; 8/9 ; 1/6
D) 2/9 ; 7/9 ; 1/6
E) 2/9 ; 7/8 ; 5/6
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 4 :
Pepe y Ramón pueden acceder a las oficinas que se muestran pudiendo estar ambos en una misma oficina. Determina la probabilidad de que dos oficinas queden vacías.
A) 3I4
B) 3I5
C) 2I3
D) 1I3
E) 1I9
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 5 :
Se tienen cuatro figuras de papel y cada una se corta en tres partes. Todas las partes se ponen en una caja y se sacan al azar 3 de ellas. ¿Cuál es la probabilidad de que las tres sean de la misma figura?
A) 1/55
B) 3/22
C) 2/55
D) 4/33
E) 3/77
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 6 :
Pedrito quiere llamar a 8 amigos para preguntarles un dato. Si solo 2 de ellos saben el dato, ¿cuál es la probabilidad de no conseguir el dato, si se sabe que solo tiene saldo para 4 llamadas?
A) 5/21
B) 3/14
C) 3/7
D) 5/14
E) 7/8
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 7 :
En una caja hay 2 medias rojas y 2 medias azules. Si se extrae dos medias al azar, ¿cuál es la probabilidad de obtener dos del mismo color?
A) 1/5
B) 1/2
C) 1/4
D) 1/6
E) 1/3
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 8 :
Se lanzan dos dados, uno azul y uno rojo. ¿Cuál es la probabilidad de que el resultado del dado rojo sea mayor al del dado azul?
A) 5/24
B) 7/12
C) 11/12
D) 3/12
E) 5/12
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 9 :
Una urna contiene 7 llaves de las cuales solo una de ellas abre una puerta. Si las llaves se prueban una por una, sin reposición, ¿cuál es la probabilidad de que la llave elegida en el cuarto intento sea la que abre la puerta?
A) 0,28
B) 0,14
C) 0,32
D) 0,23
E) 0,55
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 10 :
En una heladería tienen 12 sabores diferentes entre los cuales se encuentran maracuyá y lúcuma. Si un cliente elige 8 sabores diferentes, ¿cuál es la probabilidad de que elija maracuyá y lúcuma entre sus 8 sabores?
A) 14/33
B) 7/11
C) 2/3
D) 3/4
E) 7/9
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 11 :
Si se tiene una caja con 24 monedas, conformadas por monedas de 5 céntimos, 10 céntimos y 20 céntimos. Además la probabilidad de extraer una moneda de 5 céntimos es 3/8 y la probabilidad que sea de 10 céntimos es 1/8. Halla la cantidad de monedas de 20 céntimos.
A) 10
B) 15
C) 8
D) 11
E) 12
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 12 :
Una ruleta se ha dividido en 6 partes iguales. ¿De cuántas maneras se podrá ubicar un smartphone y las frutas piña, plátano, mango, sandía y papaya en la ruleta, con la condición que las frutas mango y papaya no están ubicados de manera contigua?
A) 68
B) 72
C) 80
D) 64
E) 81
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 13 :
En un examen las notas pueden ir desde cero hasta diez. Si tres alumnos dan dicho examen, calcule la mayor y la menor de las siguientes probabilidades:
I. Que los tres saquen la misma nota.
II. Que los tres saquen notas diferentes.
III. Que dos saquen notas iguales y otro diferente.
A) II es la menor
B) I es la mayor
C) III es la menor
D) II es la mayor
E) III=II
RESOLUCIÓN :
Rpta. : "D"
PROBLEMAS PROPUESTOS CON RESPUESTAS AL FINAL
PREGUNTA 1 :
De 100 pacientes examinados respecto a las enfermedades asma y neumonía se sabe que 20 padecen asma, 32 padecen neumonía y 8 padecen ambas enfermedades. Si se selecciona un paciente al azar, ¿cuál es la probabilidad de que no padezca estas enfermedades?
A) 0,56
B) 0,44
C) 0,62
D) 0,54
E) 0,55
PREGUNTA 2 :
Para el examen final de estadística I, se tiene un problema que dice: En una urna se tienen 12 fichas con numeración par y 8 con numeración impar. Si se escoge al azar tres fichas, ¿cuál es la probabilidad de que las tres sean impares?
A) 7/95
B) 14/285
C) 28/57
D) 13/315
E) 11/284
PREGUNTA 3 :
La probabilidad de aprobar Comunicación es del 0.80, la de aprobar Matemáticas del 0.75 y la de aprobar Inglés es del 0.70. Calcule la probabilidad de desaprobar solo uno de los cursos mencionados.
A) 0,422
B) 0,427
C) 0,430
D) 0,425
E) 0,448
PREGUNTA 4 :
Si se tiene fichas numeradas del uno al cuarenta, de las cuales se extrae al azar una y resulta par, ¿cuál es la probabilidad de que sea múltiplo de tres?
A) 0,18
B) 0,24
C) 0,27
D) 0,30
E) 0,42
PREGUNTA 5 :
El informe del SENAMHI sobre el fin de semana largo especifica: la probabilidad de que llueva; nieva o haya neblina es de: 0,40; 0,35 y 0,25 respectivamente, según esto la probabilidad que ocurra un accidente cuando llueva, nieva o haya neblina es de 0,30; 0,20 y 0,10 respectivamente. ¿Cuál es la probabilidad de que ocurra un accidente el fin de semana largo?
A) 0,60
B) 0,625
C) 0,215
D) 0,720
E) 0,845
PREGUNTA 6 :
Se desea escoger al azar un comité de 5 personas de un grupo conformado por 6 varones y 4 mujeres. ¿Cuál es la probabilidad de que en dicho comité estén por lo menos dos mujeres?
A) 31/42
B) 37/43
C) 33/41
D) 31/47
E) 32/43
PREGUNTA 7 :
Para la elaboración de placas de autos se tiene cinco vocales y 10 dígitos. Si se escoge al azar cinco caracteres diferentes para elaborar una placa, ¿cuál es la probabilidad que los tres primeros sean vocales y las dos últimos sean dígitos?
A) 15/143
B) 5/1008
C) 15/1001
D) 15/901
E) 1/42
PREGUNTA 8 :
La probabilidad de comprar una camisa es de 5/11 y la de comprar un par de pantalones es de 4/11 y la de comprar los dos artículos es de 2/11. ¿Cuál es la probabilidad de no comprar ambos artículos?.
A) 7/13
B) 3/41
C) 4/11
D) 13/28
E) 2/11
PREGUNTA 9 :
Tres caballos Andrés, Blanco y Carmelo participan en una carrera donde no hay empates. El suceso “Andrés vence a Blanco” se designa por AB, el suceso “Andrés vence a Blanco, el cual vence a Carmelo” como ABC, y así sucesivamente.
Se sabe que P(AB) = 2/3, P(AC) = 2/3 y P(BC) = 1/2.
Además P(ABC) = P(ACB), P(BAC) = P(BCA) y P(CAB) = P(CBA).
Calcular P(A venza).
A) 1/3
B) 5/9
C) 2/9
D) 2/3
E) 3/5
PREGUNTA 10 :
Un monedero contiene 2 monedas de 5 soles y 3 de un sol, y otro contiene 4 de 5 soles y 3 de un sol. Si se elige un monedero al azar y se extrae una moneda, ¿cuál es la probabilidad de que sea de 5 soles?
A) 15/37
B) 12/35
C) 17/35
D) 17/37
E) 14/37
PREGUNTA 11 :
El 30% de los estudiantes de un Instituto juega el fútbol, el 40% juega el baloncesto y el 10% juega ambos deportes. Si se elige un estudiante al azar, halle el valor de verdad de las siguientes proposiciones:
I. La probabilidad de que no juegue fútbol ni baloncesto es 0,4.
II. Si juega fútbol, la probabilidad de que juegue baloncesto es 1/3.
III. El jugar fútbol y baloncesto no son sucesos independientes.
A) VVV
B) VVF
C) FVF
D) VFV
E) FVV
PREGUNTA 12 :
Se lanzan dos dados perfectos. ¿Cuál es la probabilidad de obtener 7 o 11 puntos en las caras superiores?
A) 11/36
B) 5/7
C) 7/9
D) 3/8
E) 2/9
PREGUNTA 13 :
En la asignatura de Cálculo I se ha decidido aprobar a aquellos que aprueben uno de los dos exámenes (parcial y final). Con este criterio aprobó el 85%, sabiendo que el parcial lo aprobó el 55% y el final el 40%. ¿Cuál hubiese sido el porcentaje de aprobados, si se hubiese exigido aprobar ambos exámenes?
A) 10 %
B) 30 %
C) 60 %
D) 5 %
E) 6 %
PREGUNTA 14 :
Para obtener la licencia de conducir es necesario aprobar el examen teórico como el práctico. Se sabe que la probabilidad de aprobar la teoría es 0,85, la parte práctica es 0,75 y que se apruebe las dos partes es de 0.66. Si se elige un candidato al azar. Determine la probabilidad de que haya desaprobado los dos exámenes.
A) 0,02
B) 0,06
C) 0,03
D) 0,18
E) 0,11
PREGUNTA 15 :
Un lote consiste de 12 objetos, 8 de los cuales se califican como E (éxito) y el resto se califican con F (fracaso). Si se escogen 4 objetos al azar, uno por uno sin reposición, la probabilidad de que tres sean E y uno F es:
A) 224/495
B) 124/595
C) 54/125
D) 334/595
E) 72/125
PREGUNTA 16 :
Dos máquinas A y B producen 100 y 200 tornillos respectivamente. Se sabe que A producen el 5% de defectuosos y B el 6%. Si se toma una pieza al azar y resulta defectuosa, halle la probabilidad que procede de A.
A) 3/29
B) 5/17
C) 15/83
D) 13/95
E) 217/300
PREGUNTA 17 :
En un aula hay seis niñas y diez niños. Si se escoge un comité de tres personas al azar, halle la probabilidad de:
─ Seleccionar tres niños.
─ Seleccionar exactamente dos niños y una niña.
─ Seleccionar por lo menos un niño. De cómo respuesta la suma de los resultados.
A) 3/14
B) 27/28
C) 27/56
D) 93/56
E) 29/42
PREGUNTA 18 :
En una rifa de 2000 boletos, se tiene como premios: 5 boletos de $ 20 cada uno, 2 boletos de $ 300 cada uno y un boleto de $ 600. Si los otros no obtienen premio alguno, calcule la probabilidad de ganar alguno de los premios.
A) 0,001
B) 0,004
C) 0,020
D) 0,005
E) 0,023
PREGUNTA 19 :
Un examen consta de 14 temas, se debe escoger un tema de dos elegidos al azar. Calcule la probabilidad de que un alumno que ha estudiado 5 temas, le toque al menos uno que sabe.
A) 13/81
B) 60/91
C) 11/91
D) 50/81
E) 6/13
PREGUNTA 20 :
La prevalencia de la diabetes es del 4%. La glucemia basal diagnostica correctamente el 95% de los diabéticos, pero da un 2% de falsos positivos. Diagnosticada una persona, ¿cuál es la probabilidad de que realmente sea diabética?
A) 16/25
B) 19/286
C) 64/125
D) 32/125
E) 1/25
CLAVES – RESPUESTAS : 1)A 2)B 3)D 4)D 5)C 6)A 7)C 8)C 9)B 10)C 11)A 12)E 13)A 14)B 15)A 16)B 17)D 18)B 19)B 20)B
