PRISMAS Y PIRÁMIDES PROBLEMAS RESUELTOS GEOMETRÍA DEL ESPACIO PDF
Continuando con el estudio de los sólidos geométricos, en esta sesión desarrollaremos lo referente al prisma, una figura de bastante uso en las edificaciones arquitectónicas, seguramente por su sencillez y rigidez al momento de la construcción, además de poder adoptar diferentes bases, ésta característica hace que el arquitecto pueda idear los más impresionantes e imponentes diseños.
Así mismo esta forma suele ser muy útil en la construcción de diques para la contención de las aguas de una cierta zona geográfica para su posterior uso. Entonces debemos tener en cuenta la importancia de esta forma geométrica en la realidad como también su frecuencia en los distintos exámenes de admisión.
SUPERFICIE PRISMÁTICA
Dada una línea poligonal plana no secante a sí misma y una recta secante al plano en algún punto de dicha poligonal; la superficie prismática se genera mediante el desplazamiento de la recta por todos los puntos de la poligonal, manteniéndose siempre paralela a dicha recta en su posición inicial.
A la poligonal se le denomina directriz y a la recta que genera la superficie, generatriz.
PRISMA
Llamaremos prisma , al sólido limitado por la superficie prismática cerrada y por dos planos paralelos secantes a dicha superficie.
Las generatrices que pasan por los vértices del plano directriz se llaman aristas.
El conjunto de generatrices que pasan por los puntos de un mismo lado de la generatriz forman una cara.
Los polígonos paralelos y congruentes ABCDE y A'B'C'D'E' se llaman bases y las distancias entre ellas aristas básicas.
Los lados de dichos polígonos se denominan aristas básicas, la distancia entre las bases en la altura del prisma. Las caras restantes se denominan caras laterales.
Notación: Prisma hexagonal. ABCDEF - A´B´C´D´E´F´
SECCIÓN TRANSVERSAL :
Es la sección plana determinada en el prisma por un plano paralelo a su base.
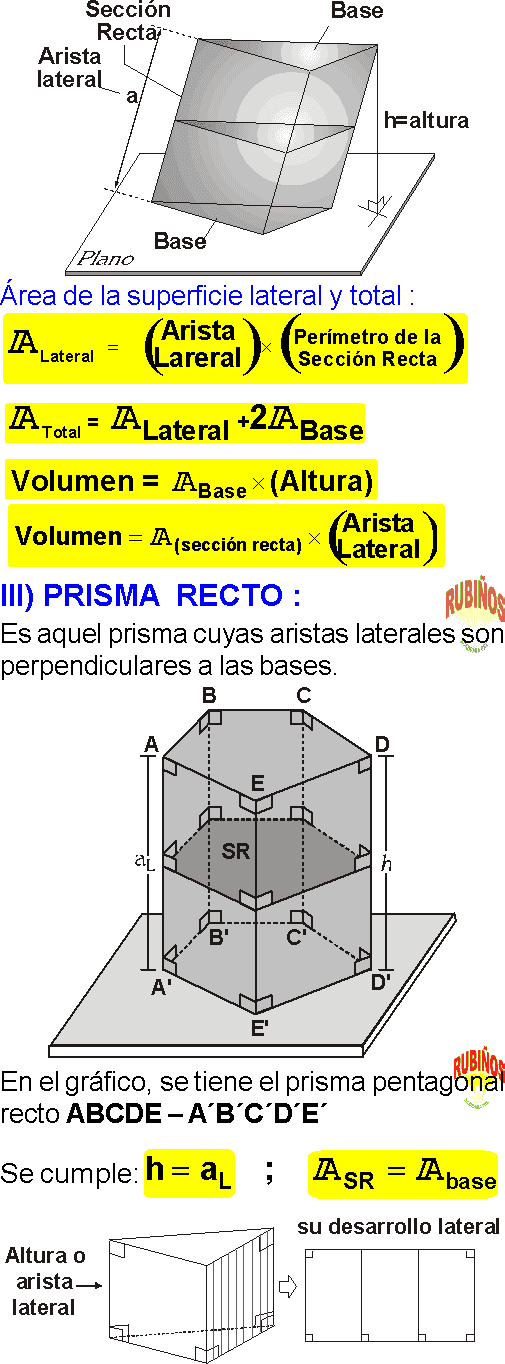
SECCIÓN RECTA :
Es la sección determinada en el prisma por un plano perpendicular y secante a todas sus aristas laterales.
DEFINICIÓN DE PRISMA :
Es aquel poliedro determinado por una superficie prismática cerrada y dos planos paralelos entre si y secante a todas las generatrices.
El prisma tiene dos caras paralelas y congruentes a las cuales se les denomina bases y la distancia entre estas es la altura del prisma, las otras caras son regiones paralelográmicas y estas son denominadas caras laterales.
Toda arista contenida en alguna base del prisma es denominada arista básica y el lado en común entre dos caras laterales es una arista lateral, todas las aristas laterales son paralelas y de igual longitud. Los prismas se nombran según el número de lados que tanga la base, por ejemplo: si tiene siete lados, se le denomina prisma heptagonal.
CLASIFICACIÓN
I) PRISMA REGULAR :
Es aquel prisma recto cuyas bases son regiones poligonales regulares.
II) PRISMA OBLICUO :
Es aquel prisma cuyas aristas laterales no son perpendiculares a las bases. .
SUPERFICIE PIRAMIDAL
Si se considera una línea poligonal plana denominada directriz y un punto exterior a dicho plano denominado vértice, entonces, una recta denominada generatriz que se mueve pasando por este punto y apoyándose constantemente sobre el polígono, genera una superficie denominada piramidal.
PIRÁMIDE
La pirámide es un poliedro limitado por un ángulo poliedro y un plano que corta todas sus aristas en puntos distintos del vértice.
La altura de la pirámide es la distancia del vértice al plano de la base.
Criterios análogos a los utilizados en prismas permiten también clasificar las pirámides en:
• Pirámides rectas y oblicuas
• Pirámides regulares e irregulares
• Pirámides de base triangular, cuadrangular, pentagonal, hexagonal, etc.
La pirámide es el sólido limitado por una superficie piramidal cerrada y un plano que interseca a todas las aristas de una hoja.
La región correspondiente al polígono de la sección se denomina base de la pirámide, el vértice de la superficie se denomina vértice o cúspide de la pirámide y la parte de superficie piramidal correspondiente a la pirámide se denomina superficie lateral de la pirámide.
Las pirámides se clasifican según número de lados de su base en pirámides triangulares, cuadrangulares , pentagonales, hexagonales, etc.
Si las bases están limitadas por un triángulo, cuadrilátero, pentágono, hexágono, etc.
También se clasifican en pirámides convexas y no convexas, según que la base sea convexa o no convexa.
*
*
EJERCICIO 1 :
Según los siguientes enunciados, indique la secuencia correcta de verdad (V) o falsedad (F) según corresponda.
I. Las bases de un tronco de prisma no pueden ser iguales.
II. La sección recta de un tronco de prisma es semejante a la base de dicho tronco de prisma.
III. El segmento que une los centroides de las bases no siempre se calcula como el promedio de un tronco de prisma, siempre es paralelo a las aristas laterales.
A) FFV
B) VVV
C) VVF
D) FVF
E) VFV
EJERCICIO 2 :
En un tronco de prisma cuadrangular cuya sección recta es cuadrada, la diagonal de esta sección es igual a 2 y la longitud de dos aristas laterales opuestas son iguales a 8 y 3. Calcule el volumen de dicho sólido.
A) 20√2
B) 11
C) 22√2
D) 32√2
E) 33√2
EJERCICIO 3 :
El área de la sección recta de un tronco de prisma triangular es 20 𝑢² y la distancia entre los centros de gravedad de las bases es 12. Calcule el volumen de dicho sólido.
A) 480 𝑢³
B) 120 𝑢³
C) 420 𝑢³
D) 120√2 𝑢³
E) 240 𝑢³
EJERCICIO 4 :
Las tres dimensiones de un paralelepípedo rectángulo suman 14. Si una de ellas es el doble de otra y el área total del prisma es máxima, determine la tercera dimensión de este sólido.
A) 3
B) 4
C) 5
D) 6
E) 7
EJERCICIO 5 :
Se tiene una pirámide cuadrangular regular en la cual una arista lateral y la altura forman un ángulo cuya medida es 30°. Calcular la medida del ángulo diedro que forma el plano de la base y un plano perpendicular a una arista lateral.
a) 45°
b) 53°
c) 37°
d) 60°
e) 30°
EJERCICIO 6 :
En una pirámide de base rectangular el pie de su altura es el punto de intersección de las diagonales, el área de la cara DVC es 5u², AD = 6u y el diedro que determina la cara AVB y la base mide 53°. Calcule el volumen de la pirámide.
a) 16 u³
b) 15
c) 12
d) 17
e) 18
EJERCICIO 7 :
Un tronco de pirámide equivalente a un hexaedro regular tiene como altura a la arista del hexaedro regular. Hallar el área total del hexaedro conociendo que el tronco de pirámide tiene por bases 1m² y 4m².
a) 13 m²
b) 9
c) 14
d) 15
e) 16
EJERCICIO 8 :
Una plancha rectangular de 3 por 5 a 4 m del piso, proyecta una sombra de 60 m² , por un foco que está encima y a "x" metros del piso. Calcular "x".
a) 5
b) 6
c) 7
d) 8
e) 9
EJERCICIO 9 :
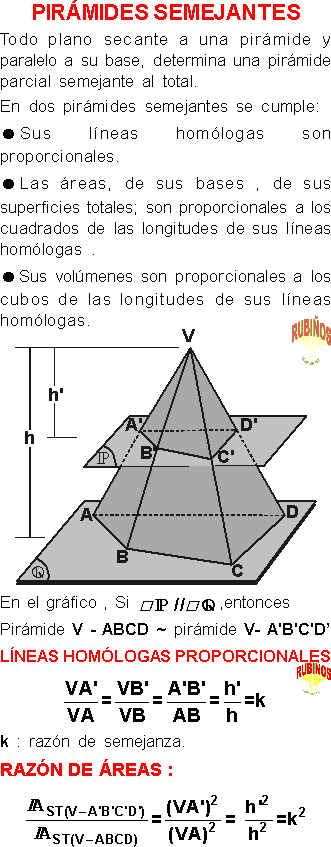
Se tiene una pirámide triangular de volumen 81 m³ y base 9 m². Calcular el volumen de la pirámide menor formada por un plano secante paralelo a la base y que determina una sección de 4 m².
a) 24 m³
b) 18
c) 16
d) 20
e) 27


































































































.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)

