MÍNIMO COMÚN MÚLTIPLO EJERCICIOS RESUELTOS DE MCM PDF
¿Qué es el mínimo común múltiplo ?
Es el menor múltiplo positivo común de varios números.
DEFINICIÓN
Dado un conjunto de cantidades se define el MCD de estas como aquel que cumple lo siguiente:
𝑖) Es un múltiplo común de las cantidades.
𝑖𝑖) Es el menor de estos múltiplos comunes.
Los múltiplos comunes de un conjunto de cantidades son múltiplos de su MCM.
El MCM es un número que contiene a los números.
EJERCICIO 1 :
El MCM de 9; 18 y 36 es :
A) 24
B) 36
C) 48
D) 54
E) 27
Rpta. : "B"
EJERCICIO 2 :
El MCM de 15 ; 75 y 90 es :
A) 5
B) 10
C) 15
D) 20
E) 25
Rpta. : "C"
EJERCICIO 3 :
¿Cuál es el mayor?
I) MCM (147; 105)
II) MCM (60; 80; 9)
III) MCM (49; 15)
A) I
B) II
C)III
D) I y II
E) I y III
Rpta. : "E"
EJERCICIO 4 :
Calcule el MCM de 126 ; 54; 108 y 378
A) 378
B) 756
C) 765
D) 75
E) 125
Rpta. : "B"
EJERCICIO 5 :
Determinar el MCM de los cuatro primeros números primos.
A) 210
B) 30
C) 1155
D) 120
E) 60
Rpta. : "A"
PRACTICA
PREGUNTA 1 :
¿Cuántos múltiplos comunes de 3 cifras tienen 60 ; 24 y 80 ?
A) 1
B) 2
C) 3
D) 4
E) 5
PREGUNTA 2 :
El MCM de 18k ; 12k y 10k es 1980. Calcular el valor de ‘‘k’’.
A) 10
B) 12
C) 11
D) 9
E) 15
PREGUNTA 3 :
¿Cuántos divisores tiene el MCM de 604 y 423?
A) 720
B) 640
C) 840
D) 900
E) 960
PREGUNTA 4 :
El producto de dos números es 2880 y su MCM es 360. Calcular su MCD.
A) 12
B) 10
C) 8
D) 9
E) 15
PREGUNTA 5 :
El MCM de 2 números primos entre sí es 340 y su suma es 37. Calcular su diferencia.
A) 1
B) 2
C) 3
D) 4
E) 5
PREGUNTA 6 :
Dos números son entre sí como 95 es a 152 y su MCM es 840. ¿Cuál es el mayor?
A) 152
B) 160
C) 168
D) 176
E) 184
PREGUNTA 7 :
Calcular el valor de ‘‘n’’, si el MCM de los números 28×32ⁿ y 28ⁿ×32 tiene 72 divisores.
A) 2
B) 3
C) 4
D) 5
E) 6
PREGUNTA 8 :
El MCM de tres números naturales que suman 255 es 1785. Si el MCD de cada par de ellos es 17, ¿cuál es el mayor?
A) 119
B) 136
C) 153
D) 170
E) 102
PREGUNTA 9 :
Calcule el valor de ‘‘n’’, si el MCM de 72ⁿ×750 y 4×90ⁿ tiene 2 944 divisores.
A) 9
B) 2
C) 3
D) 5
E) 7
PREGUNTA 10 :
La suma de dos números es 180 y el cuadrado de su MCM es igual al cubo de su MCD. Calcule el mayor de los números.
A) 108
B) 144
C) 124
D) 132
E) 158
PREGUNTA 11 :
La suma de los cuadrados de 2 números es 10530 y su MCM es 297. Calcular la suma de la mayor cifra del menor número y una de las cifras del mayor número.
A)10
B) 12
C) 15
D)16
E) 18
PREGUNTA 12 :
Tres aviones (A , B y C) parten de una base a las 8 horas. Si A regresa cada hora y cuarto, B cada 3/4 de hora y C cada 50 minutos, se reencontrarán por primera vez en la base a las:
A) 17 h 20 min
B) 18 h 20 min
C) 15 h 30 min
D) 17 h 30 min
E) 16 h 30 min
PREGUNTA 13 :
Tres móviles (A , B y C) parten al mismo tiempo de un punto de una pista circular que tiene 240 m de circunferencia. Se desplazan con velocidades de 8; 5 y 3 m/s. ¿Cuántos minutos transcurrirán para que los tres móviles realicen el primer encuentro?
A) 240
B) 24
C) 52
D) 4
E) 16
PREGUNTA 14 :
Sabiendo que el MCM de N; N+1 y 3N es 546, calcular el MCM de N+2 y 2N+1.
A) 135
B) 140
C) 145
D) 150
E) 155
PREGUNTA 15 :
La suma de dos números es 667 y el cociente de su MCM y su MCD es 120. Dar el mayor número.
A) 232
B) 435
C) 572
D) 115
E) 552
PREGUNTA 16 :
Dos números son entre sí como 5 es a 4. Su MCD y su MCM suman 756. Calcular la mayor cifra del menor número.
A) 5
B) 9
C) 4
D) 3
E) 8
PREGUNTA 17 :
El MCM de 2 números primos relativos es 255 y su suma es 32. Calcular el número menor.
A) 17
B) 18
C) 16
D) 14
E) 15
PREGUNTA 18 :
¿Cuántos números comprendidos entre 500 y 1500 son divisibles a la vez por 4 ; 5 ; 6 y 8 ?
A) 8
B) 9
C) 10
D) 11
E) 12
PREGUNTA 19 :
La suma de 2 números es 81 y su MCM es 180. Indicar el número menor.
A) 27
B) 36
C) 45
D) 54
E) 39
PREGUNTA 20 :
El MCM de 2 números es 320. Calcular la suma de cifras del mayor, sabiendo que la diferencia entre ambos es igual a 7 veces el menor.
A) 5
B) 4
C) 3
D) 2
E) 1
PREGUNTA 21 :
La circunferencia de las ruedas delanteras y posteriores de una carreta miden 2,8 y 4,8 metros. ¿Qué distancia deberá recorrer la carreta para que las ruedas delanteras den 52 vueltas más que las posteriores?.
A) 174,72m
B) 3 494,4m
C) 729,8m
D) 1747,2m
E) 349,44m
PREGUNTA 22 :
Los clubs A , B y C se reúnen cada 3 ; 4 y 6 días respectivamente. Si la primera reunión conjunta la tuvieron el 31 de octubre de 2023, en que fechas de lo que falta del año se volverá a reunir en forma conjunta . Dar como respuesta la última fecha.
A) 31 de diciembre
B) 30 de diciembre
C) 29 de diciembre
D) 28 de diciembre
PREGUNTA 23 :
Una pista de desfile de 180m de largo está marcada con rayas transversales a la pista cada metro. Si el paso de desfile es de 80cm de longitud, con una velocidad de 3,2 m/s. ¿Cuántos tiempo transcurre hasta llegar a pisar un tercio más 3 del total de rayas que de hecho pisará , teniendo en cuenta que se empezó a desfilar en la primera raya?.
A) 22,50 s
B) 21,25 s
C) 21,20 s
D) 16,25 s
E) 21,50 s
PREGUNTA 24 :
Lenin es un niño muy goloso, tal que debe consumir 1 pastel cada 9 horas, y una gaseosa cada 5 horas necesariamente para poder sobrevivir. Si hoy domingo 27 de diciembre de 2015 ha consumido a la vez un pastel y una gaseosa exactamente a las 08h. ¿Cuál es la fecha más próxima en la que Lenin volverá a consumir un pastel y una gaseosa a la vez también domingo y a la misma hora?.
A) 14 de febrero del 2016
B) 30 de marzo del 2016
C) 6 de abril del 2016
D) 11 de abril del 2016
PREGUNTA 25 :
El MCM de 4 números consecutivos es 5460. Determinar la suma de cifras del menor de ellos, si el menor número es divisible por 3.
A) 2
B) 3
C) 5
D) 7
E) 10
PREGUNTA 26 :
Juan compró cierta cantidad de caramelos, cada caramelo costó 20 céntimos y pagó por todos ellos no más de S/.90 ni menos de S/.60. Si cuenta todos los caramelos de 8 en 8 le sobran 5, de 10 en 10 le sobran 7, y de 15 en 15 le sobran 12. ¿Cuántos caramelos compró Juan?
A) 393
B) 327
C) 423
D) 477
E)357
PREGUNTA 27 :
La suma de las cifras del MCM de: 2⁹ – 1 y 2¹² – 1 es :
A) 37
B) 36
C) 35
D) 34
E) 33
CLAVES – RESPUESTAS : 1)D 2)C 3)D 4)C 5)C 6)C 7)B 8)A 9)E 10)A 11)D 12)C 13)D 14)A 15)E 16)C 17)E 18)A 19)A 20)A 21)E 22)B 23)A 24)D 25)B 26)E 27)B
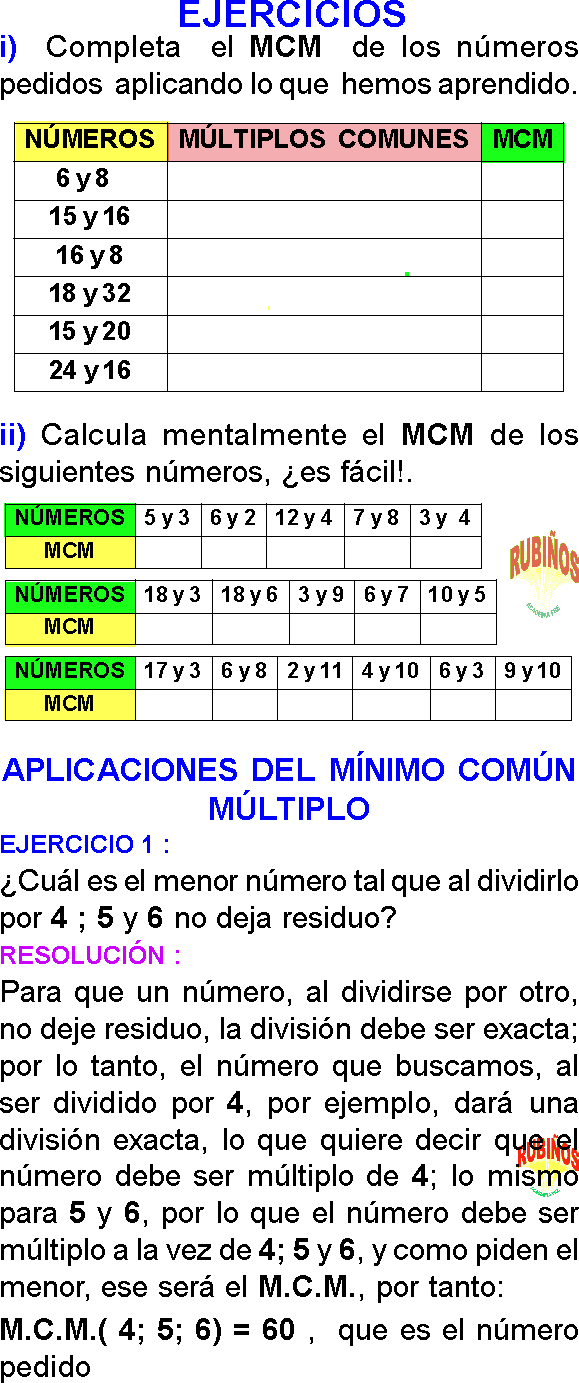
EJERCICIO 1 :
¿Cuál es el menor número tal que al dividirlo por 4 ; 5 y 6 no deja residuo?
RESOLUCIÓN :
Para que un número, al dividirse por otro, no deje residuo, la división debe ser exacta; por lo tanto, el número que buscamos, al ser dividido por 4, por ejemplo, dará una división exacta, lo que quiere decir que el número debe ser múltiplo de 4; lo mismo para 5 y 6, por lo que el número debe ser múltiplo a la vez de 4; 5 y 6, y como piden el menor, ese será el MCM, por tanto: MCM( 4; 5; 6)=60 , que es el número pedido
EJERCICIO 2 :
¿Cuál es el m.c.m. de dos números, cuyo producto es 40 y cuyo M.C.D. es 2?
RESOLUCIÓN :
No olvides que el producto de dos números es igual al de su M.C.D. por su MCM ; de acuerdo a los datos que tenemos, el MCM es un número que multiplicado por 2 (el M.C.D.) debe dar 40 (el producto de los dos números), y ese número es: 40÷2=20, que es el MCM buscado.
PREGUNTA 3 :
Las dimensiones de una barra de jabón son: 18; 12 y 10 cm. ¿Cuántas cajas cúbicas como máximo se utilizarán para empaquetar 10 800 barras, de modo que todas las cajas estén llenas?
A) 5
B) 4
C) 1
D) 2
E) 8
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 4 :
Las dimensiones (en cm) de un ladrillo para techo son las siguientes:
Un albañil desea techar una vivienda que tiene forma cuadrada, cuyo lado está comprendido entre 3 y 4 m. ¿Cuántos ladrillos como mínimo debe utilizar?
A) 360
B) 216
C) 180
D) 240
E) 32
RESOLUCIÓN :
Rpta. : "B"
PROPIEDADES DEL M.C.M. DE DOS NÚMEROS
☛ Todo múltiplo de dos números lo es de su M.C.M. y recíprocamente, todo múltiplo del M.C.M. lo es de los números.
☛ Si los dos números dados son primos entre sí, el M.C.M. es su producto.
☛ El M.C.M. de dos números de los cuales uno contiene al otro, es el mayor de ellos
☛ El producto del M.C.D. de dos números por el M.C.M. es siempre igual al producto de los números.
☛ Si dos números se multiplican por otro, su M.C.M. queda multiplicado por este otro.
Si dos números se dividen por un factor común su M.C.M. queda dividido por dicho factor.
☛ los cocientes de dividir el M.C.M. de dos números por cada uno de ellos, son primos entre sí.
