MÁXIMO COMÚN DIVISOR Y MÍNIMO COMÚN MÚLTIPLO EJERCICIOS RESUELTOS PDF
APRENDIZAJES ESPERADOS :
☛ Conocer y entender el significado de MCD y MCM
☛ Aprender los métodos comúnmente utilizados para calcular el máximo común divisor y mínimo común múltiplo.
☛ Calcular el MCD mediante el algoritmo de Euclides.
☛ Aplicar las propiedades del máximo común divisor y mínimo común múltiplo. .
La importancia del Máximo Común Divisor (MCD) y el Mínimo Común Múltiplo (MCM) radica en la aplicabilidad y en la resolución de diversos tipos de problemas matemáticos.
Una de sus mayores aplicaciones la podemos percibir en la suma y resta de números racionales de diferentes denominadores, en diversas fórmulas de física, así como en las probabilidades y mucho más; aún en cálculo superior es muy frecuente su uso. Por ende, es menester no solo comprender en qué consiste, sino saberlos calcular de manera correcta.
MÁXIMO COMÚN DIVISOR (MCD)
Es el mayor divisor común que comparten dos o más números enteros positivos.
MÍNIMO COMÚN MÚLTIPLO (MCM)
Es el menor múltiplo (positivo) común que comparten dos o más números enteros positivos.
Los múltiplos comunes de dos o más números enteros positivos son los múltiplos del MCM de dichos números.
MÉTODOS PARA EL CÁLCULO DEL MCD Y MCM
POR DESCOMPOSICIÓN CANÓNICA
Se descompone canónicamente a cada uno de los números y luego:
• El MCD es el producto de los factores primos comunes elevados cada uno a su menor exponente.
• El MCM es el producto de los factores primos comunes y no comunes elevados cada uno a su mayor exponente.
CALCULO DEL MCD POR EL ALGORITMO DE EUCLIDES
Usualmente sirve para hallar el MCD de dos números. También se le llama divisiones sucesivas.
Si conocemos los cocientes sucesivos al calcular el MCD de dos números por el algoritmo de Euclides, podemos hallar la relación de dichos números.
PRIMERA PRACTICA
EJERCICIO 1 :
El MCM de 16 ; 48 ; 96 y 15 es :
A) 420
B) 450
C) 480
D) 490
E) 500
Rpta. : "C"
EJERCICIO 2 :
El MCD de 9 ; 81 y 36 es :
A) 1
B) 3
C) 5
D) 7
E) 9
Rpta. : "E"
EJERCICIO 3 :
El MCM de 16; 48 y 96 es :
A) 96
B) 40
C) 36
D) 35
E) 108
Rpta. : "A"
EJERCICIO 4 :
El MCM de 9 ; 25 ; 50 y 81 es :
A) 2025
B) 2030
C) 1020
D) 3040
E) 9016
Rpta. : "A"
EJERCICIO 5 :
¿Cuántos divisores tiene el MCD(24;84)?
A) 2
B) 4
C) 6
D) 8
E) 10
Rpta. : "C"
EJERCICIO 6 :
¿Cuántos divisores tiene el MCM de 30 y 90?
A) 5
B) 10
C) 12
D) 20
E) 15
Rpta. : "C"
EJERCICIO 7 :
¿Cuántos divisores tiene el MCM(48 ;80)
A) 5
B) 8
C) 4
D) 9
E) 10
Rpta. : "A"
EJERCICIO 8 :
¿Cuántos divisores tiene el MCM(15;20)?
A) 10
B) 12
C) 14
D) 16
E) 18
Rpta. : "B"
EJERCICIO 9 :
Si :
MCD(8;A) = 4
MCM(8;A) =32.
Halla el valor de A.
A) 10
B) 12
C) 14
D) 16
E) 18
Rpta. : "D"
EJERCICIO 10 :
Si MCD(2k;3k)=20.
Halla el valor de “k”.
A) 5
B) 10
C) 20
D) 15
E) 30
Rpta. : "C"
EJERCICIO 11 :
Si MCM(5k;7k)=140. Halla “k”.
A) 1
B) 2
C) 3
D) 4
E) 5
Rpta. : "D"
EJERCICIO 12 :
Si :
MCD (5;A)=20
MCM(5;A)=60
Halla el valor de A.
A) 200
B) 240
C) 230
D) 210
E) 250
Rpta. : "B"
EJERCICIO 13 :
Si MCD(9k;11k)=25
Halla “k”
A) 5
B) 10
C) 15
D) 20
E) 25
Rpta. : "E"
EJERCICIO 14 :
Si MCM(7k;3k) = 189
Halla “k”
A) 1
B) 3
C) 5
D) 7
E) 9
Rpta. : "E"
SEGUNDA PRACTICA
PROBLEMA 1 :
Un tanque puede ser llenado en un número exacto de minutos por cualquiera de tres grifos que vierten 45 ; 50 y 40 litros por minuto, respectivamente. ¿Cuál es la menor capacidad que debe tener el tanque?
A) 1750 L
B) 1200 L
C) 1500 L
D) 1800 L
E) 1900 L
Rpta. : "D"
PROBLEMA 2 :
¿Cuántos múltiplos comunes de 3 cifras tienen los números 6 ; 9 y 5?
A) 14
B) 12
C) 10
D) 11
E) 8
Rpta. : "C"
PROBLEMA 3 :
El producto de 2 números es 294 y la suma de su MCD y MCM es 49. Halle la suma de los 2 números.
A) 35
B) 40
C) 42
D) 50
E) 47
Rpta. : "A"
PROBLEMA 4 :
Sean :
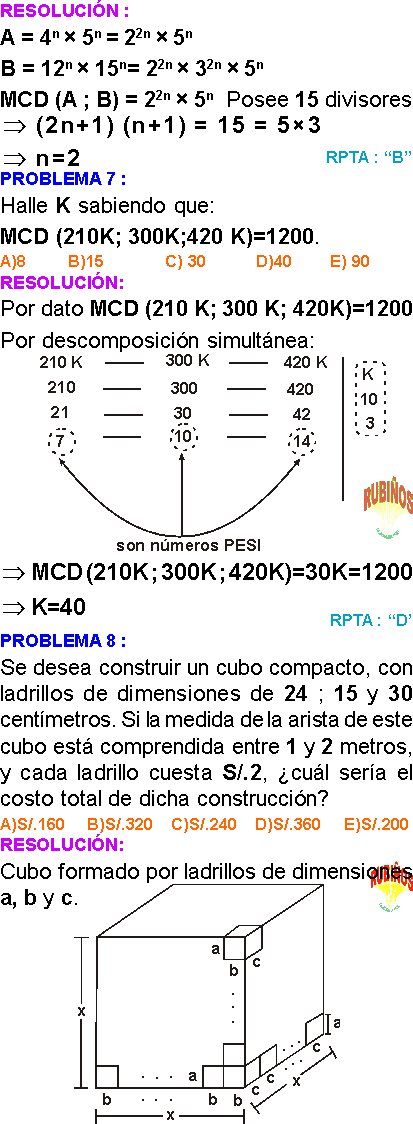
A = 4ⁿ×5ⁿ
B= 12ⁿ×15ⁿ
Si : MCD(A ; B) tiene 15 divisores determinar n.
A) 1
B) 2
C) 3
D) 4
E) 5
Rpta. : "B"
PROBLEMA 5 :
Se desea construir un cubo compacto, con ladrillos de dimensiones de 24 ; 15 y 30 centímetros. Si la medida de la arista de este cubo está comprendida entre 1 y 2 metros, y cada ladrillo cuesta S/.2, ¿cuál sería el costo total de dicha construcción?
A) S/.160
B) S/.320
C) S/.240
D) S/.360
E) S/.200
Rpta. : "B"
PROBLEMA 6 :
Una persona trata de formar un cubo de ladrillos cuyas dimensiones (del ladrillo) son 20cm ; 15cm y 8cm. Entonces, el número de ladrillos que necesita para formar el cubo más pequeño (de manera que las aristas de igual longitud sean paralelas) son.
A) 129
B) 143
C) 680
D) 2400
E) 720
Rpta. : "E"
PROBLEMA 7 :
Sea :
MCD (A ; B) = 12
A²–B² = 20880
Calcular : A – B
A) 56
B) 40
C) 82
D) 45
E) 60
Rpta. : "E"
PROBLEMA 8 :
Si :
MCD (4A ; 32C) = 24k
MCD (6C ; 3B) = 6k
MCD (A ;4B ; 8C) = 162
Calcular k
A) 64
B) 26
C) 17
D) 81
E) 9
Rpta. : "D"
PROBLEMA 9 :
Se tiene un mural de 5 metros de alto y 2 metros de ancho. Si se desea formar el menor número de cuadrados iguales para pintar las costumbres de nuestro Perú ; además no debe sobrar ni faltar espacio. Calcule la cantidad de cuadrados que se forman ; si los lados son números enteros de metros.
A) 8
B) 4
C) 2
D) 5
E) 10
Rpta. : "E"
PROBLEMA 10 :
Si para viajar a una ciudad A, dos empresas de transporte brindan dicho servicio a partir de las 6:00 a.m, la primera empresa sale cada 4 horas y las segunda empresa cada 3 horas y media . Dentro de cuánto tiempo coincidirán en la salida .
A) 5 horas
B) 28 horas
C) 4 horas
D) 24 horas
E) 48 horas
Rpta. : "B"
PROBLEMA 11 :
Si : MCM (a ; b) =91125 , calcule n.
Si :
A = 5ⁿ×9²
B = 5²×9ⁿ
A) 4
B) 7
C) 3
D) 5
E) 6
Rpta. : "C"
PROBLEMA 12 :
¿Cuántos valores toma N,si MCD(N;80)= 40? N es un número positivo de 3 cifras.
A) 10
B) 11
C) 12
D) 23
E) 21
Rpta. : "B"
PROBLEMA 13 :
Determine el mínimo volumen que debe tener una caja cúbica para empaquetar jabones, cuyas dimensiones son : 6cm×8cm×15cm, sin que sobre espacio .
A) 1, 296 m³
B) 1, 458 m³
C) 2, 744 m³
D) 1, 964 m³
E) 1, 728 m³
Rpta. : "E"
PROBLEMA 14 :
Se tiene 3 varillas metálicas de 72 cm , 108 cm y 120 cm. Se desea tener la menor cantidad de varillas más pequeñas de cantidad entera de centímetros cortando todas las anteriores de igual tamaño. ¿Cuántos varillas pequeñas se tendría?
A) 20
B) 24
C) 25
D) 30
E) 18
Rpta. : "C"
PROBLEMA 15 :
Se han plantado árboles igualmente espaciados en el contorno de un campo cuadrangular cuyos lados miden 144 m, 120 m, 84 m y 180 m sabiendo que hay un árbol en cada vértice y que la distancia entre 2 árboles consecutivos está comprendido entre 4 m y 10 m. Calcule el número de árboles plantados
A) 60
B) 56
C) 40
D) 44
E) 88
Rpta. : "E"
PROBLEMA 16 :
Se tiene 3 listones de madera de 144 cm, 84 cm y 150cm cada uno , los cuales se desea cortar en listones más pequeños de tal manera que todos sean de la misma longitud (entera en centímetros). ¿De cuántas maneras se puede realizar?
A) 5
B) 2
C) 3
D) 4
E) 7
Rpta. : "D"
PROBLEMA 17 :
Andrea tiene una cartulina que mide 24 cm de ancho por 36 cm de largo y quiere cortar trozos cuadrados de manera que no sobre material. ¿Cuántos trozos obtendrá , si el lado de cada uno mide una cantidad entera , comprendidos entre 5 cm y 10 cm?
A) 10
B) 6
C) 24
D) 12
E) 18
Rpta. : "C"
PROBLEMA 18 :
Lenin trabaja cinco días seguidos y descansa el sexto día; en cambio Carolina trabaja cuatro días seguidos y descansa el quinto día. Si ambos comienzan a trabajar el día lunes, ¿cuántos días tiene que trabajar cada una de ellos para que les toque descansar un domingo simultáneamente? . Dé como respuesta la suma de ambas cantidades.
A) 360 días
B) 343 días
C) 240 días
D) 390 días
E) 400 días
Rpta. : "C"
PROBLEMA 19 :
Calcule la suma de dos números primos entre sí, tal que se diferencien en 7 y su MCM sea 330.
A) 35
B) 25
C) 37
D) 34
E) 40
Rpta. : "C"
PROBLEMA 20 :
Si la suma de dos enteros positivos es 2 880 , si tienen 15 divisores comunes ¿Cuál es la menor diferencia de dicho enteros ?
A) 259
B) 201
C) 864
D) 288
E) 416
Rpta. : "D"
PROBLEMA 21 :
Al calcular el MCD de 2 números mediante el algoritmo de Euclides, los cocientes sucesivos fueron 2 ; 5 ; 3 ; 2 . Calcule la diferencia de los números , si sabe que son primos relativos.
A) 54
B) 44
C) 30
D) 53
E) 42
Rpta. : "B"
PROBLEMA 22 :
El máximo común divisor de 2 números es 9 . ¿Cuál es el mínimo común múltiplo de dichos números, si su producto es 1620 ?.
A) 180
B) 20
C) 270
D) 1620
E) 400
Rpta. : "A"
PROBLEMA 23 :
Se trata de formar un cubo de ladrillos cuyas dimensiones son 20 centímetros , 15 centímetros y 6 centímetros. ¿Cuántos ladrillos son necesarios para formar el cubo más pequeño posible?
A) 100
B) 140
C) 120
D) 160
E) 180
Rpta. : "C"
PROBLEMA 24 :
Se tiene un jardín de forma rectangular cuyas dimensiones son : 1 104m y 960m ; se quiere dividir en parcelas cuadradas todas iguales sin que sobre terreno y luego se desea cercarlas , de tal manera que exista un poste en cada esquina de las parcelas, indicar la menor cantidad de parcelas y la menor cantidad de postes que se necesitarán para cercar todas las parcelas.
A) 460 y 480
B) 480 y 504
C) 480 y 525
D) 460 y 504
E) 4560 y 500
Rpta. : "D"
PROBLEMA 25 :
Se desea usar un recipiente para llenar 3 botellas cuyas capacidades son medio litro , 650 mililitros y de 4/5 de litro ¿Cuántas veces como mínimo será necesario echar el recipiente lleno en cada botella de modo que no sobre ni falte líquido?.
A) 36
B) 195
C) 130
D) 49
E) 39
Rpta. : "E"
PROBLEMA 26 :
Se sabe que la diferencia entre el MCM y MCD de 3 números es 897, que la diferencia entre mayor, y el intermedio es 26 y con el menor es 65 ¿Cuál de los siguientes números es uno de ellos?.
A) 52
B) 78
C) 91
D) 117
E) 130
Rpta. : "C"
PROBLEMA 27 :
Tres obreros tienen que colocar losetas en un área de 535m2. Y demoran 30 ;36 y 45 minutos por metro cuadrado respectivamente. ¿Cuántas horas tardarán en culminar dicho trabajo , si se desea que cada uno emplee un mínimo de tiempo y cubra cada uno , un número exacto de metros cuadrados al mismo tiempo?.
A) 21 h
B) 42 h
C) 96 h
D) 105 h
E) 140h
Rpta. : "D"
PROBLEMA 28 :
¿Cuántos son los 2 números primos entre sí , cuyo MCM es 330 y su diferencia es 7?.
A) 55 y 46
B) 22 y 29
C) 18 y 25
D) 22 y 15
E) 14 y 21
Rpta. : "D"
PROBLEMA 29 :
El MCD de 2 números A y B es 248 y el menor de ellos es 2976 . Sabiendo que MCM está comprendiendo entre 59520 y 89500 . ¿Cuántas soluciones hay para el mayor de dichos números ?.
A) 2
B) 4
C) 5
D) 3
E) 1
Rpta. : "D"
PROBLEMA 30 :
Hallar los números A y B si se sabe que satisfacen :
A²+ B² = 10530
MCM (A ; B) = 297
A) 11 y 27
B) 99 y 27
C) 27 y 33
D) 81 y 97
E) 83 y 91
Rpta. : "B"
PROBLEMA 31 :
Se tiene dos números que son los menores posibles en el sistema heptanario , cuya suma de cifras son 216 y 324 respectivamente. Calcular la suma de sus cifras del MCD de dichos números expresados en el sistema de base 49.
A) 432
B) 324
C) 423
D) 342
E) 454
Rpta. : "A"
PROBLEMA 32 :
Las ruedas delanteras de una locomotora tiene 27cm. de radio y las pares de ruedas traseras 52cm. de radio; las ruedas de los vagones del tren al que está enganchado tiene 43cm de radio ¿Al cabo de cuántas vueltas de las traseras, todas las ruedas tomarán la misma posición?.
A) 1161
B) 1302
C) 981
D) 1253
E) 971
Rpta. : "A"
PROBLEMAS RESUELTOS
PREGUNTA 1 :
El M.C.M. de las edades de dos hermanos es el doble de la edad del mayor y el M.C.D. es la tercera parte de la edad del mayor. ¿Qué edad tiene el mayor, si el menor tiene ocho años?
A) 15
B) 12
C) 6
D) 18
E) 9
RESOLUCIÓN :
Rpta. : "B"