MÁXIMO COMÚN DIVISOR EJERCICIOS RESUELTOS MCD PDF
¿Qué es máximo común divisor?
Es el mayor de los divisores comunes de varios números
DEFINICIÓN DE MCD
Dado un conjunto de cantidades se define al MCD de estas como aquel número que cumple las siguientes condiciones:
𝑖) Es un divisor común de las cantidades
𝑖𝑖) Es el mayor de los divisores comunes
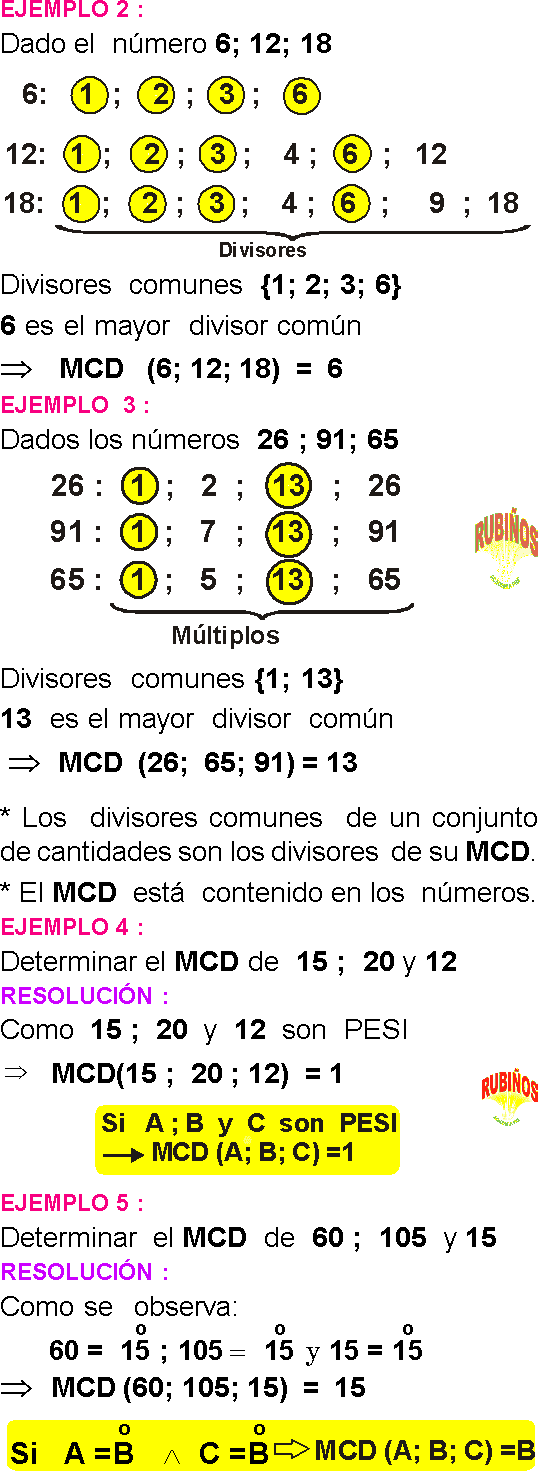
EJERCICIO 1 :
El MCD de 490 y 3500 es :
A) 20
B) 30
C) 40
D) 60
E) 70
Rpta. : "E"
EJERCICIO 2 :
El MCD de 50 y 175 es :
A) 25
B) 20
C) 15
D) 10
E) 5
Rpta. : "A"
EJERCICIO 3 :
¿Cuál es el menor?
I) MCD (66; 374)
II) MCD (54; 216)
III) MCD (198; 286)
A) I
B) II
C) III
D) I y II
E) I y III
Rpta. : "E"
EJERCICIO 4 :
Calcule el MCD de 390 ; 585 ; 780 y 975
A) 15
B) 25
C) 195
D) 75
E) 125
Rpta. : "C"
EJERCICIO 5 :
Determinar el MCD de (30×16) y de (21×18)
A) 3
B) 2
C) 6
D) 9
E) 12
Rpta. : "C"
PRACTICA PROPUESTA
PREGUNTA 1 :
¿Cuántos divisores comunes tienen los números 720 ; 400 y 360 ?
A) 10
B) 12
C) 6
D) 9
E) 8
PREGUNTA 2 :
El MCD de 24k ; 60k y 84k es 132. Calcular el valor de ‘‘k’’.
A) 12
B) 4
C) 33
D) 11
E) 66
PREGUNTA 3 :
¿Cuántos divisores tiene el MCD de 183 y 305?
A) 24
B) 20
C) 18
D) 16
E) 25
PREGUNTA 4 :
¿Cuántos números de 3 cifras existen tales que tengan con 864 un MCD igual a 72?
A) 5
B) 2
C) 3
D) 4
E) 6
PREGUNTA 5 :
El MCD de 21A y 35B es 42k. Calcular el MCD de 15A y 25B.
A) 24k
B) 25k
C) 30k
D) 36k
E) 35k
PREGUNTA 6 :
Se han plantado árboles igualmente espaciados en el contorno de un campo triangular cuyos lados miden 144; 180 y 240 metros. Sabiendo que hay un árbol en cada vértice, ¿cuántos árboles como mínimo se utilizarán?
A) 47
B) 48
C) 46
D) 45
E) 49
PREGUNTA 7 :
Al dividir 2007 y 666 entre ‘‘n’’ los residuos respectivos fueron 63 y 18. Calcular el mayor valor de ‘‘n’’.
A) 64
B) 72
C) 90
D) 108
E) 80
PREGUNTA 8 :
¿Cuántos pares de números suman 476 y tienen como MCD a 28?
A) 1
B) 6
C) 8
D) 13
E) 16
PREGUNTA 9 :
El producto de 2 números es 5915 y el MCD de ellos es 13. Calcular el mayor, si ambos son menores que 100.
A) 65
B) 91
C) 83
D) 78
E) 93
PREGUNTA 10 :
Determinar dos números tales que su MCD es 11 y la diferencia de sus cuadrados es 2904. Dar el número de soluciones.
A) 0
B) 1
C) 2
D) 3
E) 4
PREGUNTA 11 :
¿Cuántos números menores que 80 tienen con 360 un MCD igual a 4?
A) 6
B) 2
C) 3
D) 5
E) 4
PREGUNTA 12 :
Se desea dividir 3 barras de acero de longitudes 165; 225 y 345 cm, en trozos de igual longitud. ¿Cuál es el menor número de trozos que se pueden obtener?
A) 40
B) 44
C) 55
D) 47
E) 49
PREGUNTA 13 :
Un comerciante de vinos tiene 3 barriles de 540; 960 y 1260 litros de capacidad. Desea vender este vino en recipientes todos iguales, cuya capacidad esté comprendida entre 25 y 48 litros, además están contenidos exactamente en cada uno de los barriles. Calcule el número de recipientes necesarios.
A) 48
B) 92
C) 46
D) 42
E) 23
PREGUNTA 14 :
Calcular la suma de 2 números enteros cuyo MCM es 22400 y tales que en el cálculo del MCD mediante divisiones sucesivas se obtuvieron como cocientes 2 ; 5 y 3.
A) 2 040
B) 2 240
C) 2 050
D) 2 250
E) 2 060
PREGUNTA 15 :
Calcular la suma de dos números, sabiendo que su MCD es 144 y que tienen 33 y 35 divisores.
A) 11 664
B) 20 800
C) 9 216
D) 5 280
E) 20 880
PREGUNTA 16 :
¿Cuántos pares de números existen cuyo MCD sea 13 y su producto sea 2028?
A) 1
B) 2
C) 3
D) 4
E) 5
PREGUNTA 17 :
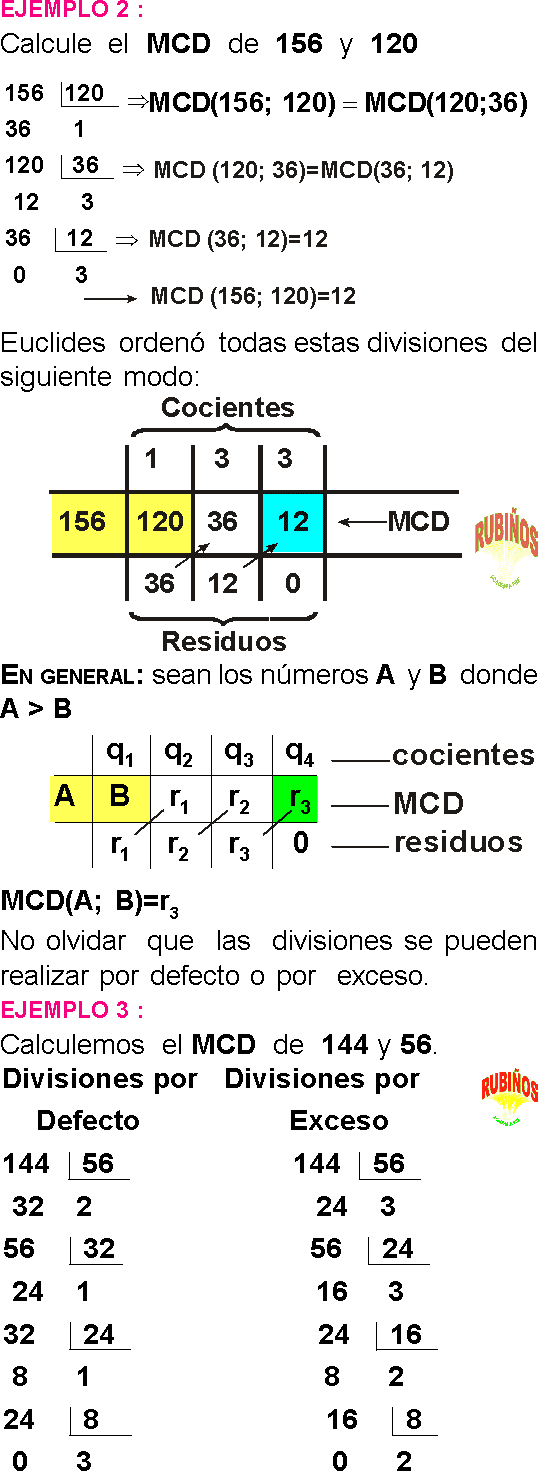
Determinar la suma de los cocientes obtenidos al calcular el MCD de 364 y 840 mediante el Algoritmo de Euclides.
A) 6
B) 7
C) 8
D) 9
E) 10
PREGUNTA 18 :
Las dimensiones de un terreno rectangular son 1288 y 952m. Se desea parcelarlo en terrenos cuadrados de modo que no sobre terreno y se obtenga el menor número de parcelas. Si en cada esquina de éstas se coloca un poste, ¿cuántos postes se necesitarán?
A) 421
B) 452
C) 556
D) 432
E) 426
PREGUNTA 19 :
¿Cuántos divisores comunes tienen los números 420; 360 y 1260?
A) 12
B) 10
C) 8
D) 6
E) 4
PREGUNTA 20 :
Al calcular el MCD de 2 números por el Algoritmo de Euclides se obtuvieron los cocientes sucesivos: 2; 5; 3 y 2. Calcular dicho MCD, si la diferencia de los números es 880.
A) 20
B) 25
C) 16
D) 28
E) 14
PREGUNTA 21 :
El producto de dos números enteros positivos es 360. La suma de los cocientes obtenidos al dividir cada uno de ellos por su máximo común divisor es 7, y el producto de estos cocientes es 10. Entonces, el valor de la diferencia de estos números es:
A) 2
B) 31
C) 18
D) 84
E) 54
PREGUNTA 22 :
¿Cuántos pares de números cumplen la condición de que su MCD sea 7 y el producto entre ellos 1470?.
A) 2
B) 3
C) 4
D) 5
E) 7
PREGUNTA 23 :
Hallar el mayor factor común a los números (6550 – 1) , (6252 – 1) y (6312 – 1)
A) 5
B) 11
C) 23
D) 31
E) 35
PREGUNTA 24 :
El número A tiene 21 divisores y el número B tiene 10 divisiones. Si el máximo común divisor de A y B es 18 , entonces A+B es:
A) 654
B) 738
C) 756
D)792
E) 810
PREGUNTA 25 :
Si el MCD de 36 y 120 es n, entonces el MCD de 24; 90 y n² es:
A) 8
B) 6
C) 1
D) 2
E) 3
CLAVES – RESPUESTAS : 1)E 2)D 3)A 4)D 5)C 6)A 7)B 8)C 9)B 10)C 11)A 12)E 13)B 14)A 15)E 16)B 17)D 18)D 19)A 20)A 21)C 22)C 23)E 24)B 25)B
EJERCICIO 1 :
En una bolsa hay 30 galletas de soda, 36 de vainilla y 42 de chocolate. Si las reparto entre mis amigos de tal manera que a cada uno le toque la misma cantidad de galletas de cada clase, ¿a cuántos amigos como máximo les podré repartir las galletas, sin que sobren ni falten galletas?
RESOLUCIÓN :
Fíjate que debo repartir las 30 galletas de soda (por ejemplo) entre mis amigos, y para que a todos les toque la misma cantidad, sin sobrar ni faltar, debo tener tantos amigos que pueda dividir las 30 galletas exactamente, es decir, el número de amigos que tengo es DIVISOR de 30; lo mismo se aplica para las 36 de vainilla y las 42 de chocolate. Conclusión: el número de amigos que tengo es divisor común de 30; 36 y 42, y como quiero la máxima cantidad, será el M.C.D., por ello:
M.C.D.(30; 36; 42) = 6 son los amigos que tengo
PREGUNTA 2 :
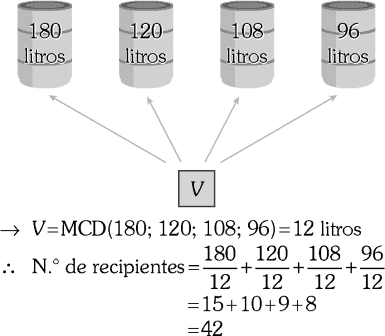
En un almacén hay cuatro barriles de 180, 120, 108 y 96 litros de capacidad, los cuales están llenos de aceite, y se desea envasarlos en recipientes pequeños de máxima capacidad. ¿Cuántos recipientes se necesita para que no sobre aceite en ninguno de los barriles?
A) 42
B) 36
C) 24
D) 48
E) 12
RESOLUCIÓN :
Rpta. : "A"