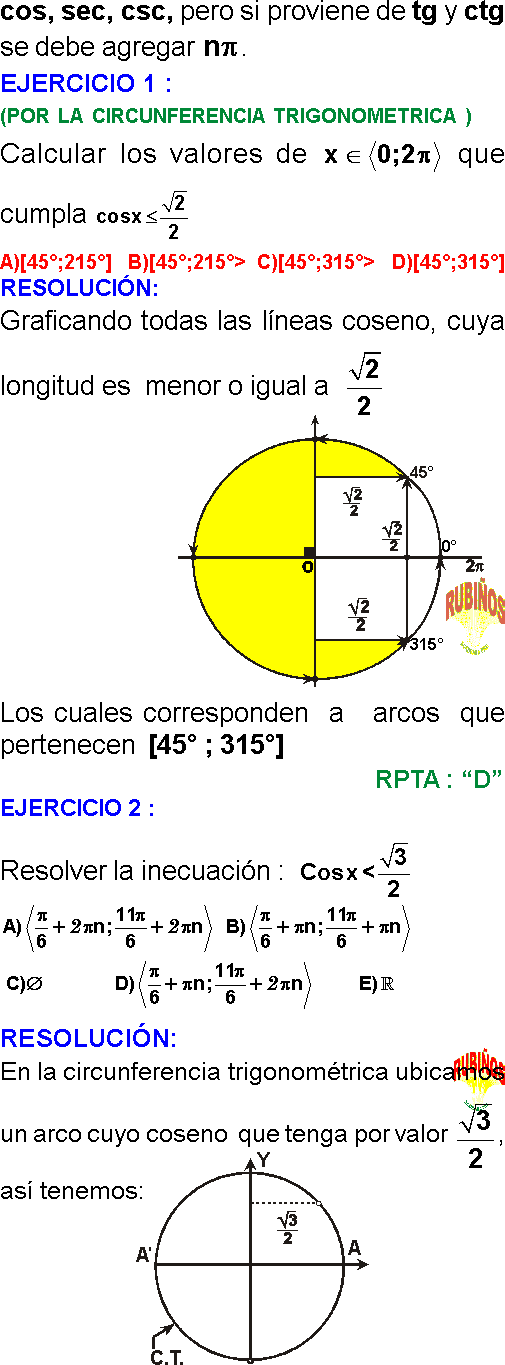
INECUACIONES TRIGONOMÉTRICAS EJERCICIOS RESUELTOS PDF
¿QUÉ ES UNA INECUACIÓN TRIGONOMÉTRICA ?
Se denomina inecuación trigonométrica a toda desigualdad entre funciones trigonométricas que se va o no a verificar para un conjunto de valores de la variable , si la inecuación se verifica se llamará compatible en caso contrario incompatible.
APRENDIZAJES ESPERADOS :
☛ Resolver inecuaciones trigonométricas
☛ Conocer la definición de la inecuación trigonométrica
☛ Conocer y resolver la inecuación trigonométrica elemental.
☛ Conocer los mecanismos y estrategias para poder resolver una inecuación no elemental y un sistema de inecuaciones trigonométricas
☛ Aplicar lo aprendido en la resolución de ejercicios
Se entiende por conjunto solución de una inecuación, como el conjunto de valores de la incógnita (o incógnitas) para los cuales es cierta la desigualdad.
Recordemos los teoremas mencionados en el punto anterior , asociado con la representación en la circunferencia trigonométrica nos ayuda a calcular una variable con una expresión sencilla. Sin embargo cuando el problema resulta difícil de reducir entonces debes considerar el siguiente razonamiento.
SOLUCIONES DE LA INECUACIÓN TRIGONOMÉTRICA
A todo valor o intervalo de valores de la variable o incógnita que verifique la relación planteada se llamará solución de la inecuación y al conjunto formado por la unión de todas las soluciones de la inecuación se le llamará conjunto solución de dicha inecuación.
RESOLUCIÓN DE INECUACIONES TRIGONOMÉTRICAS
Resolver una inecuación trigonométrica consiste en determinar todas sus soluciones; es decir determinar su conjunto solución, para lo cual se utilizará la circunferencia trigonométrica como herramienta de análisis en la cual se observará el recorrido del arco que verifica la inecuación, así como también se empleará la gráfica de las funciones presentes en la relación planteada y sus respectivas intersecciones.
PREGUNTA 1 :
Resuelva la inecuación:
Sen2x≥0
RESOLUCIÓN :
Ubicamos en la C.T. el recorrido del arco que verifica la relación, es decir todo el recorrido donde sen2x sea mayor o igual que cero, colocando 2x en dicho recorrido, de donde se despejará el intervalo de x que nos representará la solución de la relación planteada.
PREGUNTA 2 :
Resuelva la inecuación
RESOLUCIÓN :
Se grafica cada uno de los miembros de la inecuación como una función independiente; es decir graficaremos: