PROBLEMAS DE IDENTIDADES TRIGONOMÉTRICAS RESUELTOS PREUNIVERSITARIOS PDF
IDENTIDADES TRIGONOMÉTRICAS BÁSICAS DEL MISMO ARCO
IDENTIDAD TRIGONOMÉTRICA
Una identidad trigonométrica es una igualdad que contiene expresiones trigonométricas que se cumplen para cualquier valor admisible de la variable.
Ejemplos:
Identidad algebraica :
(a+b)² = a² + 2ab + b²
Identidad Trigonométrica :
sen²θ + cos²θ = 1
Ecuación Trigonométrica :
senθ + cosθ = 1
Para : θ = 90º cumple
Para : θ = 30º no cumple
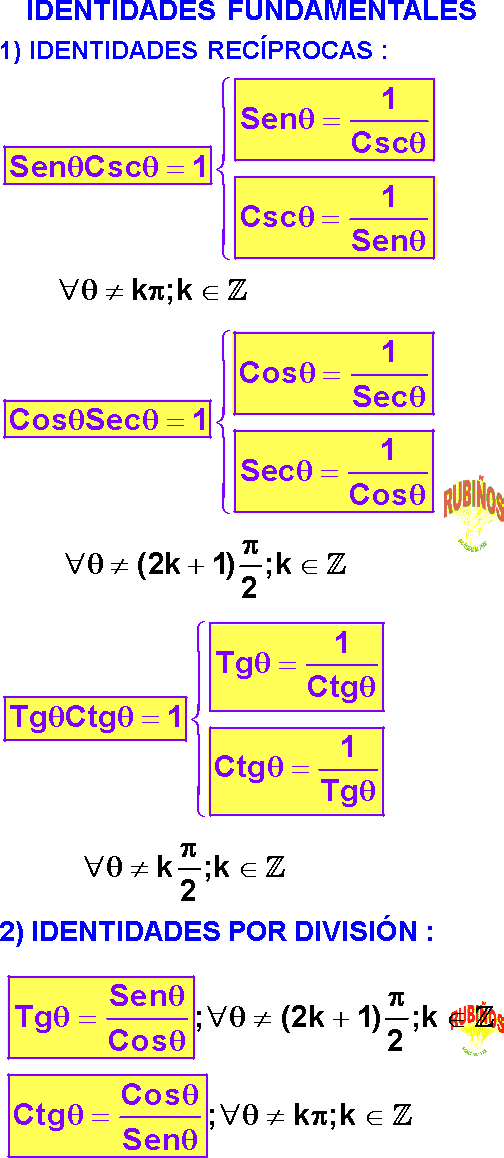
IDENTIDADES FUNDAMENTALES
Las identidades trigonométricas fundamentales sirven de base para la demostración de otras identidades más complejas.
Se clasifican en:
IDENTIDADES PITAGÓRICAS
sen²x + cos²x = 1
sec²x = 1 + tg²x
csc²x = 1 + ctg²x
IDENTIDADES POR COCIENTE
tgx =senx÷cosx
ctgx=cosx÷senx
IDENTIDADES RECÍPROCAS
senxcscx = 1
tgxctgx = 1
secxcosx = 1
Observaciones :
sen²x = 1 – cos²x
sen²x = (1 + cosx) (1 – cosx)
cos²x = 1 – sen²x
cos²x = (1 + senx)(1 – senx)
Los ejercicios en este capítulo son de tipo demostración, simplificación.
Para resolverlos se requiere un manejo eficiente de las identidades ya mencionadas.
AUXILIARES CONDICIONALES Y DEMOSTRACIONES DE FÓRMULAS
En una identidad trigonométrica la variable angular es la misma para todas las razones trigonométricas.
PROBLEMAS PROPUESTOS
PREGUNTA 1 :
Reduce : secx – tanx.senx
a) senx
b) cscx
c) cosx
d) secx
e) 1
Rpta. : "C"
PREGUNTA 2 :
Si: Tanx + Cotx = 3
Calcula: Tan³x + Cot³x
A) 15
B) 16
C) 17
D) 18
E) 19
Rpta. : "D"
PREGUNTA 3 :
Si: Senx + Cosx = √2
Calcula: Sen⁴x + Cos⁴x
A) 1
B) 1/2
C) -1
D) -1/2
E) 2
Rpta. : "B"
PREGUNTA 4 :
Si:
1 + Tanx = Usecx
1 – Tanx = VSecx
Halla : U² + V²
A) 1
B) 2
C) 1/2
D) 3
E) 1/4
Rpta. : "B"
PREGUNTA 5 :
Si: Cosx + Cos²x = 1
Calcula: Sen²x + Sen⁴x
A) 1
B) 2
C) 3
D) 4
E) 5
Rpta. : "A"
PREGUNTA 6 :
Simplifica :
Sen²xCos²x(Sec²x + Csc²x)
a) 1
b) 1/2
c) 2
d) Senx
e) Cosx
Rpta. : "A"
PREGUNTA 7 :
Si : Ctgx – Cosx = 4
Calcula: 4Tgx + Senx
A) 0
B) 1
C) 2
D) 4
E) 8
Rpta. : "B"
PREGUNTA 8 :
Cscx – Senx = a
Secx – Cosx = 2ª
Halla Tgx
A) √2
B) ∛2
C) 2
D) ∛3
E) 1
Rpta. : "B"
PREGUNTA 9 :
Si Tgx – Ctgx = 6
Calcula Tg²x + Ctg²x
A) 2
B) 4
C) 6
D) 8
E) 10
Rpta. : "D"
PREGUNTA 10 :
Simplifica :
(Senx + Cosx)(Cosx – Secx)(Tgx + Ctgx)
a) –1
b) 1
c) 0
d) 2
e) 3
Rpta. : "B"