GEOMETRÍA EJERCICIOS RESUELTOS PDF
PROBLEMAS RESUELTOS DE GEOMETRÍA DE SECUNDARIA PREUNIVERSITARIA Y EXAMEN DE ADMISIÓN A LA UNIVERSIDAD
PREGUNTA 1 :
En la figura, determina x
A) 13°
B) 25°
C) 20°
D) 50°
E) 45°
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 2 :
La altura de un triángulo equilátero es la mitad de la diagonal de un cuadrado de lado 5 m. Halle la razón de las áreas determinadas por el triángulo y el cuadrado.
A) √3/6
B) √3/7
C) √3/8
D) 3/5
E) √3/3
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 3 :
En el trapecio ABCD, determina la longitud AD si BC= 6 y CD= 9.
A) 17
B) 15
C) 13
D) 16
E) 19
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 4 :
En un triángulo de perímetro 12 m, está inscrita una circunferencia de radio 1 m. Halle la diferencia entre las áreas que determinan el triángulo y la circunferencia (en m²).
A) 3 – 𝛑
B) 6 – 𝛑
C) 4 – 𝛑
D) 5 – 𝛑
E) 8 – 𝛑
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 5 :
En la figura, AM² + BN² = 63 cm² y NC² + MB² = 145 cm². Halle el valor de AC.
A) 6√13
B) √13
C) 3√13
D) 2√13
E) 4√13
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 6 :
En la figura ABCD es un cuadrado. Si el área del triángulo APQ=18 u², calcula la longitud AT. T: Punto de tangencia
A) 6 u
B) 4 u
C) 8 u
D) 12 u
E) 9 u
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 7 :
En la figura O es el centro de la semicircunferencia. Si OA=6 cm, medida del arco BC=100° y medida del arco CD=40°. Halle el área de la región sombreada.
A) 10𝛑 cm²
B) 18𝛑 cm²
C) 15𝛑 cm²
D) 16𝛑 cm²
E) 20𝛑 cm²
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 8 :
En la figura adjunta, AM= MC= CB. ¿Cuál es el valor del ángulo x?
A) 37°
B) 30°
C) 60°
D) 37°/2
E) 53°
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 9 :
En el gráfico, determine el arco PQ.
A) 10°
B) 15°
C) 25°
D) 10°
E) 30°
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 10 :
Los lados de un triángulo miden 3, 4 y 5 metros. Halle el radio de la circunferencia exinscrita al lado menor.
A) 1 m
B) 3 m
C) 2 m
D) 5 m
E) 2/3 m
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 11 :
En un polígono regular, se pueden trazar desde 4 vértices consecutivos 17 diagonales. Calcule la medida del ángulo externo.
A) 45°
B) 60°
C) 75°
D) 54°
E) 30°
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 12 :
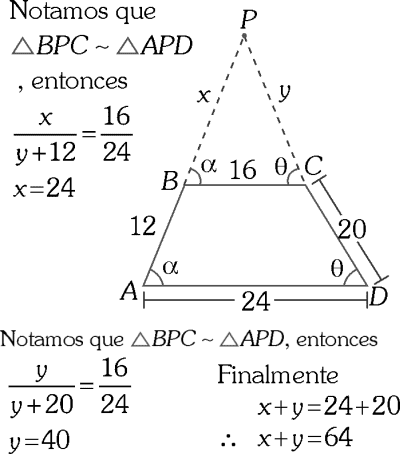
En la figura, ABCD es un trapecio (BC//AD) las prolongaciones de AB y DC se intersecan en un punto P. Calcula: PB+PC
A) 60
B) 64
C) 56
D) 54
E) 72
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 13 :
En la figura, OA es diámetro. Calcule la ecuación de la recta ℓ.
A) 3x + y – 20 = 0
B) x – y – 20 = 0
C) x + 3y + 20 = 0
D) 3x + y + 20 = 0
E) 3x – y – 18 = 0
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 14 :
¿Para qué valores de k la recta ℓ : y=kx – 1 interseca la parábola x²=8y?
RESOLUCIÓN :
Rpta. : "D"
EJERCICIOS DE SEGMENTOS CON RESPUESTAS
PREGUNTA 1 :
Sobre una recta se ubican los puntos consecutivos “A”, “B” y “C”. Tal que “M” es punto medio de AC. Calcula “BM”. Si: BC = AB + 40.
a) 5
b) 8
c) 12
d) 20
e) 30
Rpta. : "D"
PREGUNTA 2 :
Sobre una recta se ubican los puntos consecutivos A, B y C tales que AB = 10 y BC = 8. Si “M” es punto medio de AB. Calcula “MC”.
a) 11
b) 12
c) 13
d) 14
e) 15
Rpta. : "C"
PREGUNTA 3 :
Los puntos colineales y consecutivos A, B, C y D son tales que: AD = 18, BD = 13 y AC = 12. Calcula “BC”.
a) 3
b) 4
c) 5
d) 6
e) 7
Rpta. : "E"
PREGUNTA 4 :
Sobre una recta se ubican los puntos consecutivos “A”, “B”, “C” y “D” tal que: CD = 4AC, si BD – 4AB = 20. Calcula “BC”.
a) 2
b) 3
c) 5
d) 7
e) 4
Rpta. : "E"
PREGUNTA 5 :
Sobre una recta se ubican los puntos consecutivos “A”, “B”, “C” y “D”.
Si se cumple: AB/2=BC/3=CD/5
Calcula “CD”, si: AD = 20
a) 12
b) 9
c) 6
d) 10
e) 8
Rpta. : "D"
EJERCICIOS DE TRIÁNGULOS CON RESPUESTAS
PREGUNTA 1 :
Dos lados de un triángulo miden 7 y 9. Calcula el mayor valor entero del perímetro del triángulo.
a) 30
b) 31
c) 32
d) 33
e) 34
Rpta. : "B"
PREGUNTA 2 :
Dos lados de un triángulo miden 6 y 8. Calcula el mayor valor entero del tercer lado.
a) 10
b) 11
c) 12
d) 13
e) 14
Rpta. : "D"
PREGUNTA 3 :
Las medidas de los ángulos externos de un triángulo se encuentran en progresión aritmética. Calcula la medida de uno de los ángulos internos de dicho triángulo.
a) 30°
b) 60°
c) 40°
d) 50°
e) 27°
Rpta. : "B"
PREGUNTA 4 :
La suma de las medidas de dos ángulos internos de un triángulo es 110 y su diferencia es 10. Calcula la medida del menor ángulo interno de este triángulo.
a) 10°
b) 20°
c)30°
d) 40°
e) 50°
Rpta. : "E"
PREGUNTA 5 :
Dos lados de un triángulo miden 3 y 4 el tercer lado es el doble de uno de estos dos lados. ¿Cuánto mide el tercer lado?
a) 6
b) 8
c) 16
d) 12
e) 10
Rpta. : "A"
PREGUNTA 6 :
En un triángulo ABC, AB = 2, BC = 5. Calcula la suma de los valores pares que puede tomar “AC”.
a) 8
b) 9
c) 10
d) 12
e) 18
Rpta. : "C"
PREGUNTA 7 :
Dos lados de un triángulo isósceles miden 6 y 15. Calcula el perímetro del triángulo.
a) 30
b) 27
c) 36
d) 42
e) 28
Rpta. : "C"
PREGUNTA 8 :
Los lados de un triángulo miden 3; x + 9; 2x – 6.Calcula el mayor valor entero que puede tomar “x” para que el triángulo exista.
a) 17
b) 18
c) 19
d) 16
e) 15
Rpta. : "A"
EJERCICIOS DE POLÍGONOS CON RESPUESTAS
PREGUNTA 1 :
Calcula la suma de los ángulos interiores de un decágono.
a) 180°
b) 1260°
c) 540°
d) 1440°
e) 900°
Rpta. : "D"
PREGUNTA 2 :
¿Cuántas diagonales tiene un octágono?
a) 14
b) 20
c) 27
d) 35
e) 44
Rpta. : "B"
PREGUNTA 3 :
Si la suma de los ángulos internos de un polígono es 1260°,¿cuántas diagonales tiene el polígono?
a) 90
b) 20
c) 27
d) 35
e) 54
Rpta. : "C"
PREGUNTA 4 :
¿En qué polígono, el número de diagonales es igual al número de lados?
a) Pentágono
b) Icoságono
c) Hexágono
d) Decágono
e) Endecágono
Rpta. : "A"
PREGUNTA 5 :
Calcula el número de lados de aquel polígono en el cual su número de lados más su número de diagonales es 28.
a) 5
b) 6
c) 7
d) 8
e) 10
Rpta. : "D"
