CILINDRO Y CONO DE REVOLUCIÓN PROBLEMAS RESUELTOS GEOMETRÍA DEL ESPACIO PDF

CILINDRO 

Es aquel sólido geométrico comprendido entre dos planos paralelos entre si y secantes a una superficie curva cerrada denominada superficie lateral del cilindro y en los planos paralelos se determinan secciones planas congruentes las cuales se denominan bases del cilindro. 

En la superficie lateral del cilindro se ubican segmentos paralelos entre si y congruentes, cuyos extremos son los puntos del contorno de las bases, dichos segmentos se denominan generatrices. 

SECCIÓN AXIAL DE UN CILINDRO DE REVOLUCIÓN 

Es una sección plana determinada en el cilindro por un plano que contiene a su eje. 

DESARROLLO DE LA SUPERFICIE LATERAL DE UN CILÍNDRO DE REVOLUCIÓN : 

Resulta una región rectangular en la cual uno de sus lados tiene igual longitud de la circunferencia de una base y el otro lado es de igual longitud de la generatriz del cilindro .

Para construir objetos cilindros (pote de conservas, tarros de leche, recipientes para pinturas), es necesario hacer el diseño en una plancha de latón y luego realizar el corte correspondiente. Tal como se muestra en la figura. 

CILINDRO CIRCULAR RECTO 

Es aquel cilindro recto cuyas bases son círculos. 

También es denominado cilindro de revolución porque es generado por una región rectangular al girar una vuelta en torno a uno de sus lados. 

CILINDRO OBLICUO DE SECCIÓN RECTA CIRCULAR 

Es aquel cilindro oblicuo cuya sección recta es un círculo. 

Las bases del cilindro oblicuo de sección recta circular son regiones elípticas cuyas áreas se calculan en función de sus semiejes. 

TRONCO DE CILÍNDRO 

Es la porción del cilindro comprendida entre una base y un plano secante a todas sus generatrices no paralelo a sus bases.

*

*

SUPERFICIE CÓNICA 

Es la superficie que se genera por una recta denominada GENERATRIZ al ser desplazada a través de una línea curva plana denominada DIRECTRIZ y pasando siempre por un punto fijo no coplanar con dicha directriz. 

SUPERFICIE CÓNICA DE REVOLUCIÓN 

Se llama superficie cónica de revolución a aquella superficie generada por una recta que intersectando al eje en un punto fijo, gira alrededor de dicho eje, formando con él un ángulo invariable. 

CONO : 

Es aquel sólido geométrico que a semejanza de la pirámide tiene un vértice o cúspide con la diferencia de que su base es una región curva en lugar de una poligonal. 

El cono circular recto es aquel sólido que tiene como base a un círculo y cuyo pie de la altura que parte del vértice es el centro de dicho círculo. 

El cono oblicuo es el sólido que se determina al cortar a un cono recto con un plano no paralelo a su base. Su base es un elipse. 

CONO EQUILÁTERO : 

Un cono se llama equilátero cuando su generatriz es igual al diámetro de su base. 

DESARROLLO DE LA SUPERFICIE LATERAL : 

Es un sector circular que tiene por radio la generatriz del cono y por arco, la longitud de la circunferencia de la base del cono. 

SEMEJANZA DE CONOS 

Si dos conos son generados por triángulos semejantes que giran alrededor de dos lados homólogos, dichos conos son semejantes. 

También si se intersecta a un cono por un plano paralelo a la base se obtiene un cono pequeño semejante al total, debiéndose cumplir: 

I) Las áreas de sus bases son entre si como el cuadrado de las longitudes de sus elementos homólogos. 

II) Los volúmenes son entre si como el cubo de sus elementos homólogos. 

TRONCO DE CONO RECTO O DE REVOLUCIÓN 

Es el sólido que se determina al cortar a un cono recto con un plano paralelo a su base. Se puede considerar como el sólido generado por la rotación de un trapecio rectángulo del lado perpendicular a las bases. 

ÁREA DE LA SUPERFICIE LATERAL

El área lateral de un tronco de cono de revolución es igual a la suma de los semiperímetros de las bases multiplicado por la generatriz .

El área total de un tronco de cono revolución es igual a la suma del área lateral con las áreas de las bases 

VOLUMEN

El volumen de un tronco de cono de revolución de altura h y cuyos radios de las bases son R y r esta dado por la suma de sus bases y la media proporcional entre dichas bases 

SUGERENCIA : 

En los conos de revolución es adecuado trabajar con la sección axial.

PROBLEMA 1 : 

En la base de un cilindro recto de revolución se inscribe una región rectangular de área 𝕊. Halle el volumen del mayor cilindro recto en donde la generatríz es igual al doble del diámetro de la base.

PROBLEMA 2 : 

Una región rectangular de perímetro 24cm se hace girar sobre uno de sus lados que mide H cm , obteniéndose un sólido cilíndrico. La expresión para determinar el volumen del sólido obtenido, en términos de H, es: 

PROBLEMA 3 : 

Si r es el radio de la base de un cilindro con tapa, de volumen 100cm³, el área del material usado en la construcción del envase, expresado en función de r, es: 

PROBLEMA 4 : 

En un hexaedro regular ABCD – EFGH , AB = a , halle el volumen del cilindro cuyas bases están inscritas en la secciones EBD y FHC. 

PROBLEMA 5 : 

Un cilindro tiene a sus bases inscritas en dos caras opuestas de un cubo de arista a. Un plano diagonal del cubo intercepta al cilindro determinado una sección transversal cuya área se pide calcular. 

PROBLEMA 6 : 

Halle el volumen del cilindro de revolución inscrito en un octaedro regular de arista a , de modo que las bases del cilindro se encuentran contenidas en dos caras opuestas del octaedro. 

PROBLEMA 7 : 

En un prisma triangular regular se escribe un cilindro. ¿Qué relación existe entre las áreas laterales de estos dos cuerpos?. 

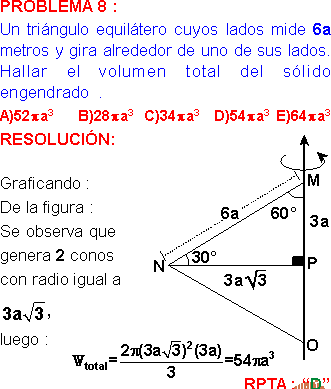
PROBLEMA 8 : 

En un tetraedro regular de arista «a» se inscribe en un tronco de cilindro recto de base circular tal que su vértice coincide con el centro de la cara superior. Calcular el volumen del tronco de cilindro. 

PROBLEMA 9 : 

De todos los cilindros circulares rectos de área total igual a 2𝜋a², halle el volumen del cilindro de máximo volumen. 

PROBLEMA 10 : 

Una cuña cilíndrica está definida por un ángulo diedro de 60º, el radio de su base r y generatriz g. Halle el área lateral.

PROBLEMA 11 : 

La fórmula del volumen del cono circular recto, en función de la generatriz g y de la altura h, es: 

PROBLEMA 12 : 

Dado un triángulo equilátero ABC, se le hace girar una vuelta alrededor de una de sus alturas, generándose un sólido de volumen V1 . Si el triángulo equilátero ABC gira una vuelta alrededor de uno de sus lados, se genera un sólido de volumen V2 . Calcular la relación V1 / V2. 

PROBLEMA 13 : 

En un cono revolución se corta una cuña cónica de ángulo central 30°. El área de la base del cono es Bu² y el área de la sección que determina un plano axial es Au². Calcule el volumen del sólido que queda. 

PROBLEMA 14 : 

Se tiene un hexaedro regular ABCD – EFGH de arista L. Halle el volumen del cono que se encuentra en el interior del hexaedro , con vértice en el punto A y base circular inscrita en el triángulo GHC. 

PROBLEMA 15 : 

Dos rectángulos congruentes de lados a y 3a tiene un lado común que mide a y forman un diedro de 30°. En uno de los rectángulos reposa la base de un cono circular, la cual es tangente a los lados mayores. Calcule el volumen de este cono , si su vértice se encuentra en el lado menor del otro rectángulo. 

PROBLEMA 16 : 

Halle el volumen del sólido limitado por un cono recto de revolución de dos hojas cuyos radios de las bases miden R y r , las bases distan H. 

PROBLEMA 17 :  

Un tronco de cono de revolución de área total A, está circunscrita a una esfera de radio R. Halle el volumen del tronco. 

PROBLEMA 18 : 

El radio de la base de un cono de revolución es R y su altura es H , se inscribe un cilindro recto de área lateral máxima. Calcule la altura y el radio del cilindro.