ÁREAS DE REGIONES TRIANGULARES EJERCICIOS RESUELTOS PDF

APRENDIZAJES ESPERADOS 

• Conocer las fórmulas básicas para calcular el área de una región triangular. 

• Deducir teoremas para calcular áreas de regiones triangulares, a partir de las fórmulas básicas. 

• Aplicar lo aprendido en la resolución de problemas tipo examen de Admisión.

En la medición de las áreas de regiones planas, se siguen empleando métodos, que son un legado de las antiguas culturas, Egipcias y también formulas de grandes matemáticos como Herón de Alejandría.

MIDIENDO SUPERFICIES 

Para medir superficies es necesario adoptar una unidad patrón y compararla con la extensión de dicha superficie. 

Recordarás que las unidades patrón de superficie : 

km², Hm², Dm², m² , dm², mm²

Sin embargo, para medir terrenos, se utilizan con frecuencia la llamada unidad agraria: Hectárea o su equivalente : 

Ha = Hm² = 10 000m²

La medida de la extensión de una superficie se llama ÁREA de dicha superficie. 

REGIONES POLIGONALES : 

Una región triangular es un conjunto de puntos, reunión de un triángulo y su interior. Una región poligonal es la reunión de un número finito de regiones triangulares que se encuentran en un plano dado, tales que si dos cualesquiera de ellas se intersecan, su intersección es o bien un punto o un segmento. 

Las líneas punteadas en las figuras anteriores indican cómo se podría representar cada una de las dos regiones poligonales mediante tal reunión. 

Las regiones triangulares de cualquier descomposición asi se llaman regiones triangulares componentes de la región poligonal. 

REGIÓN: 

Es aquella parte de una superficie plana delimitada por una línea. 

ÁREA: 

Es el número que indica la medida de una región, es decir es igual al número de veces que se utiliza la región unitaria. 

POSTULADO DE LA UNIDAD

El área de una superficie limitada por un cuadrado de lado una unidad es igual a una unidad cuadrada. 

POSTULADOS

• Dada una unidad de área, a cada región le corresponde un número único, llamado área de la región. 

• El área de una región poligonal es la suma de las áreas de cualquier conjunto de regiones componentes em el cual puede dividirse. 

• Si dos polígonos son congruentes, entonces las regiones poligonales correspondientes tienen la misma área. 

ÁREA DE REGIONES PLANAS REGIÓN PLANA : 

Es una porción de plano limitado por una línea cerrada. 

ÁREA DE UNA REGIÓN PLANA : 

Es la medida de una región plana, se toma como unidad de comparación al área de una región cuadrada cuyo lado tiene por longitud a la unidad. 

REGIONES EQUIVALENTES 

Son regiones planas que tienen igual área. 

Sus formas no son necesariamente iguales 

ÁREA DE REGIONES TRIANGULARES 

Es una región plana cuyo contorno es un triángulo. 

Estudiaremos, ahora las principales fórmulas para el cálculo de áreas de las regiones triangulares. 

FÓRMULA GENERAL : 

El área de una región triangular es igual al semi producto de las longitudes de un lado y la altura relativa a dicho lado. 

CÁLCULO DEL ÁREA DE UNA REGIÓN TRIANGULAR EN FUNCIÓN DE LA LONGITUD DE SUS LADOS : (FÓRMULA DE HERÓN) 

El área de una región triangular es igual a la raíz cuadrada del producto del semiperímetro de la región triangular y la diferencia de dicho semiperímetro con la longitud de cada uno de los lados. 

FÓRMULA TRIGONOMÉTRICA : 

El área de una región triangular es igual al semi producto de las longitudes de dos lados, multiplicado con el seno del ángulo determinado por dichos lados. 

ÁREA DE UN TRIÁNGULO EQUILÁTERO EN FUNCIÓN DEL LADO : 

El área de un triángulo equilátero es igual a la cuarta parte del cuadrado de la longitud de su lado por la raíz cuadrada de 3. 

ÁREA DE UN TRIÁNGULO EQUILÁTERO EN FUNCIÓN DE LA ALTURA : 

El área de un triángulo equilátero es igual a la tercera parte del cuadrado de la longitud de su altura por la raíz de 3. 

ÁREA DE UNA REGIÓN TRIANGULAR EN FUNCIÓN DE SU INRADIO : 

El área de un triángulo es igual al producto de su semiperímetro con el inradio del triángulo correspondiente. 

ÁREA DE UNA REGIÓN TRIANGULAR EN FUNCIÓN DE SU CIRCUNRADIO : 

El área de una región triangular es igual al cociente del producto de las longitudes de sus tres lados con el cuádruplo de su circunradio. 

ÁREA DE UNA REGIÓN TRIANGULAR EN FUNCIÓN DE SU EXRADIO : 

El área de una región triangular es igual al producto de la diferencia entre el semiperímetro y un lado cualquiera por el radio de la circunferencia ex-inscrita correspondiente a ese lado. 

ÁREA DE UNA REGIÓN TRIANGULAR EN FUNCIÓN DE SUS EX-RADIOS Y SU INRADIO : 

El área de un triángulo es igual a la raíz cuadrada del producto de los radios de las circunferencias inscritas y ex-inscritas. 

FÓRMULAS ADICIONALES 

• El área de un triángulo rectángulo es igual al producto de las longitudes de los segmentos que la circunferencia inscrita determina sobre la hipotenusa. 

• El área de un triángulo rectángulo es igual al producto de las longitudes de los segmentos que la circunferencia ex-inscrita a la hipotenusa determina sobre dicha hipotenusa. 

• El área de un triángulo rectángulo es igual al producto de las longitudes de los segmentos que la circunferencia ex-inscrita relativa a uno de los catetos determina sobre la hipotenusa.

PROBLEMAS RESUELTOS

PREGUNTA 1: 

En la figura, se tiene AM=MC, PC=3NP y el área de la región triangular ABC es 48m². Halle el área de la región sombreada MPC. 

A) 10 m² 

B) 11 m² 

C) 12 m² 

D) 14 m²

E) 15 m²

RESOLUCIÓN :

Rpta. : "C"

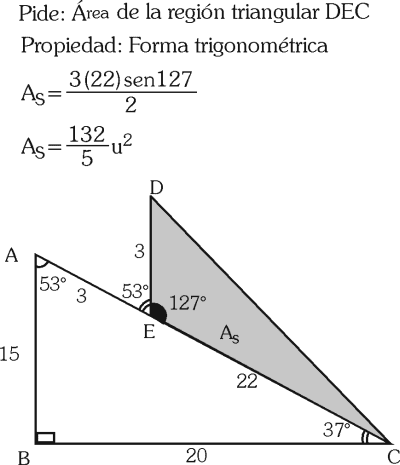
PREGUNTA 2 : 

A) 120/7 u² 

B) 132/5 u² 

C) 140/9 u²

D) 135/8 u² 

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 3 : 

En el gráfico, AB=6m y BC=8m; D y E son puntos de tangencia. Halle el área de la región sombreada

A) 10m²   

B) 16m²    

C) 8m² 

D) 6m²    

E) 12m² 

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 4 : 

Se tiene un triángulo equilátero ABC de lado 12, MN//AC . Si AM=10. 

Calcula el área de la región del triángulo ABN. 

A) 3√3 

B) 6√3 

C) 4√3 

D) 5√3 

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 5 : 

En un triángulo rectángulo recto en B, se traza la altura BH (H en AC). Si HC=28 y BH=14, calcula el área de la región triangular ABC. 

A) 230 μ²

B) 245 μ²

C) 260 μ² 

D) 250 μ² 

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 6 : 

A) 2 

B) 3 

C) 4 

D) 5 

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 7 : 

El área total del triángulo ABC es igual a 1200m². 

Las medidas de los segmentos AD y DC en metros. 

Calcula 𝕊₁ y 𝕊₂ en m². 

A) 460; 740 

B) 470; 730 

C) 480; 720 

D) 490; 710 

E) 450; 750 

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 8 : 

En un triángulo isósceles ABC, se trazan las medianas AM y CN perpendiculares. Si AC=1 y AB=BC, calcula el área de la región triangular ABC. 

A) 2 μ²

B) 3/2 μ²  

C) 3/4 μ²  

D) 3/8 μ²  

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 9 : 

En el gráfico mostrado, AM=MC, BL=LM, 𝔸ΔBLE=8μ²  , 2(EC)=3(BE) ; calcule 𝔸ΔABC. 

A) 80 

B) 70 

C) 65 

D) 64 

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 10 : 

Del gráfico mostrado, el triángulo AMD es equilátero y CD=8 u. Sean 𝔸₁ y 𝔸₂ las regiones sombreadas, calcula 𝔸₁×𝔸₂ 

A) 64 u²

B) 108/3 u² 

C)  128/3 u² 

D) 149/3 u²

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 11 :  

Del gráfico mostrado, calcule el área de la región sombreada si AC=25 , AB=24 , BC=7, M es punto medio del segmento AB y MD=13. 

A) 16 u² 

B) 15/7 u²

C) 48/7 u² 

D) 20 u² 

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 12 :

Se tienen dos triángulos equiláteros, uno inscrito y el otro circunscrito a una misma circunferencia. Si el área de la región determinada por las dos regiones triangulares es 9√3 u², calcule la longitud de la circunferencia. 

A) 3𝛑 

B) 2𝛑 

C) 4𝛑 

D) 6𝛑 

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 13 : 

En un triángulo equilátero ABC de lado 6√2, se ubican los puntos P y Q en AB y BC, respectivamente. Si PQ es paralelo a AC y las regiones determinadas son equivalentes, calcula PQ. 

A) 6 

B) 3√2 

C) 7 

D) 8 

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 14 : 

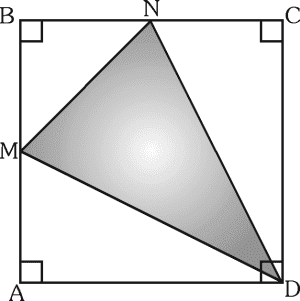
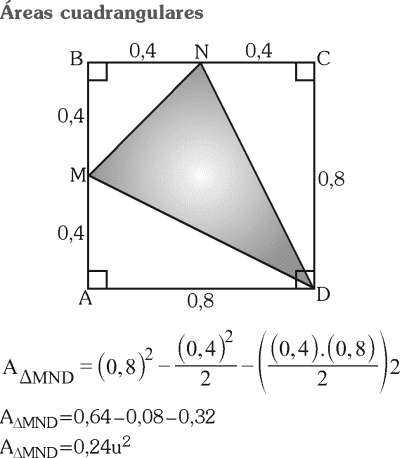
Del gráfico, si M y N son puntos medios de los segmentos AB y BC respectivamente, si AB=BC=0,8. 

Calcule el área de la región triangular MND 

A) 0,24u²  

B) 0,25u²

C) 0,26u² 

D) 0,18u²  

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 15 :  

Se tiene hexágono regular cuyo perímetro es 12√3 . Calcule el área de la región triangular cuyos vértices son los puntos medios de los lados no consecutivos. 

A) 25√3 /4

B) 27√3/4 

C) 28√3 

D) 39√3 /4

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 16 : 

Un ∆ ABC tiene por coordenadas A(–5;1) , B(–5;4) y C(2;4). Calcular el área del triángulo. 

A) 10,5 u² 

B) 12,5 u² 

C) 14,5 u² 

D) 16 u² 

RESOLUCIÓN :

Rpta. : "A"

PRACTICA

PREGUNTA 1 :

En un triángulo ABC, recto en B, cuya hipotenusa mide 12, la m∢C=15º. Calcule el área de la región ABC. 

A) 15 u² 

B) 24 u² 

C) 18 u² 

D) 36 u²

E) 28 u² 

Rpta. : "C"

PREGUNTA 2 :

En un triángulo ABC, la m∢A = 30º, m∢C = 75º y AC = 10. Calcule el área de la región ABC. 

A) 35 u² 

B) 25 u² 

C) 45 u² 

D) 32 u²

E) 26 u² 

Rpta. : "B"

PREGUNTA 3 :

Los lados de una región triangular miden 5 ; 5 y 8. Calcule la longitud del exradio relativo a uno de sus lados congruentes. 

A) 3 

B) 2 

C) 5 

D) 4 

E) 6 

Rpta. : "A"

PREGUNTA 4 :

En una región triangular sus lados miden 10 ; 21 y 17. Calcule la longitud de su inradio. 

A) 7/3 

B) 7/2 

C) 5/2 

D) 4 

E) 6/5 

Rpta. : "B"

PREGUNTA 5 :

En una región triangular sus lados miden 6 ; 7 y 8. Calcule el producto de las longitudes de su inradio y circunradio. 

A) 8 

B) 12 

C) 15 

D) 9 

E) 7 

Rpta. : "A"

PREGUNTA 6 :

Los lados de una región triangular miden 30, 30 y 48. Calcule la longitud de su circunradio. 

A) 35 

B) 25 

C) 50 

D) 24 

E) 16 

Rpta. : "B"

PREGUNTA 7 :

Los lados de una región triangular miden 5 ; 5 y 6. Calcule la longitud del exradio relativo a uno de sus lados congruentes. 

A) 5 

B) 2 

C) 3 

D) 6 

E) 4 

Rpta. : "E"

PREGUNTA 8 :

Los lados de una región triangular miden 13 ; 14 y 15. Calcule la longitud de su inradio. 

A) 3 

B) 2 

C) 5 

D) 4 

E) 6 

Rpta. : "D"

PREGUNTA 9 :

En un triángulo rectángulo ABC, recto en B, se inscribe una circunferencia tangente a la hipotenusa en Q; si AQ = 9 cm y Q = 7 cm, calcule (AB)(BC). 

A) 54 cm² 

B) 48 cm² 

C) 70 cm² 

D) 52 cm²

E) 63 cm² 

Rpta. : "E"

PREGUNTA 10 :

En un triángulo ABC, AC = 2 y BC = 4; si la altura relativa a AC mide 3, calcule la medida de la altura relativa a BC. 

A) 3 

B) 2 

C) 5 

D) 4 

E) 6 

Rpta. : "B"

PREGUNTA 11 :

En un triángulo rectángulo ABC, recto en B, se inscribe una circunferencia tangente a la hipotenusa en M. Si AM = 6 cm y MC = 4 cm, calcule (AB)(BC). 

A) 64 cm² 

B) 50 cm² 

C) 55 cm² 

D) 60 cm² 

E) 48 cm² 

Rpta. : "E"

PREGUNTA 12 :

Calcule el área de la región triangular sabiendo que el producto de las longitudes de sus lados es igual a 172 u³ y su circunradio mide 3 u. 

A) 10 u² 

B) 12 u² 

C) 15 u² 

D) 16 u² 

E) 18 u² 

Rpta. : "D"

PREGUNTA 13 :

Dado un triángulo rectángulo ABC, recto en B, se traza la altura BH la bisectriz AF interseca a BH en P. Calcule el área de la región triangular BPF si AP = 6 u y PF = 4 u. 

A) 7 u² 

B) 8 u²

C) 9 u² 

D) 10 u² 

E) 11 u² 

Rpta. : "B"

PREGUNTA 14 :

En un triángulo rectángulo, el cateto menor mide 8 m y la mediana relativa a la hipotenusa mide 8,5 m. Calcule el área de la región triangular. 

A) 50 m² 

B) 42 m² 

C) 25 m² 

D) 45 m² 

E) 64 m² 

Rpta. : "A"

PREGUNTA 15 :

Los lados AB, BC y AC de un triángulo ABC miden 8 u, 10 u y 14 u, respectivamente. Calcule el área de la región triangular ABI siendo I el incentro del triángulo ABC. 

A) 4√6 u² 

B) 4√2 u² 

C) 3√3 u² 

D) 3√2 u² 

E) 3√6 u² 

Rpta. : "A"

PREGUNTA 16 :

En un triángulo rectángulo ABC, recto en B, la altura relativa a la hipotenusa determina sobre ésta segmentos que miden 3 u y 4 u. Calcule el área de la región triangular ABC. 

A) 12 u² 

B) 7√3 u² 

C) 7 u² 

D) 6 u² 

E) 14 u² 

Rpta. : "B"

PREGUNTA 17 :

Se tiene un ángulo recto ABC donde AB = BC, se traza una semicircunferencia de diámetro AB. En dicha semicircunferencia se ubican los puntos P y Q; si BP² – BQ² = 16 u², halle el área de la región cuadrangular no convexa BPCQ (en u²). 

A) 8 u² 

B) 16 u² 

C) 32 u² 

D) 48 u² 

E) 64 u² 

Rpta. : "A"

PREGUNTA 18 :

En un triángulo rectángulo ABC, se ubica el incentro I; si AI = 3 u y CI = 4√2 , entonces el área (en u²) de la región triangular AIC es: 

A) 8 u² 

B) 6 u² 

C) 12 u² 

D) 10 u² 

E) 6√2 u² 

Rpta. : "B"

PREGUNTA 19 :

El área de una región triangular es 108 y su perímetro es 54. Calcule la longitud de su inradio. 

A) 2 

B) 4 

C) 3 

D) 6 

E) 5 

PREGUNTA 20 :

Calcule el área de una región triangular cuyos lados miden 4 ; 4 y 6. 

A) 3√7 

B) 2√7 

C) 4√7 

D) 5√7 

E) 7 

PREGUNTA 21 :

Los lados de una región triangular miden 3 ; 7 y 8. Calcule el producto de las longitudes de su inradio y circunradio. 

A) 14/9 

B) 14/3 

C) 14/5 

D) 14/11 

E) 14/13 

PREGUNTA 22 :

Los lados de un triángulo miden 9 u ; 11 u y 12 u. Calcule el área de su región. 

A) 8√11 u² 

B) 2√11 u² 

C) 4√11 u² 

D) 3√11 u²

E) 6 u² 

Rpta. : "A"

PREGUNTA 23 :

En un triángulo, dos de sus lados de 8 y 15 m respectivamente forman un ángulo de 37°, calcule el área de la región triangular. 

A) 18 m² 

B) 21 m² 

C) 24 m² 

D) 36 m² 

E) 40 m² 

PREGUNTA 24 :

Los lados de un triángulo miden 9 u ; 11 u y 12 u. Calcule el área de su región. 

A) 9√6 u² 

B) 8√35 u² 

C) 12√6 u²

D) 15√3 u² 

E) 10√5 u²

• CLIC AQUÍ Ver PDF