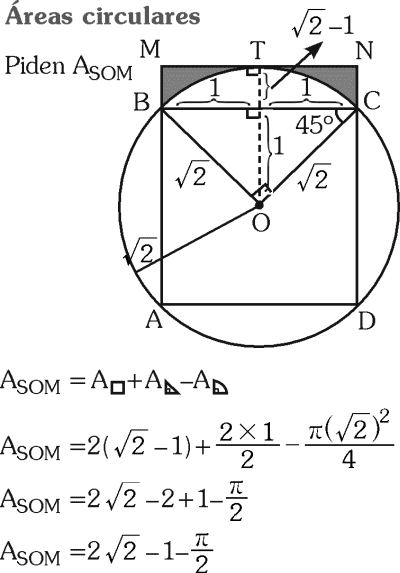ÁREAS SOMBREADAS EJERCICIOS RESUELTOS PDF RAZONAMIENTO MATEMÁTICO

OBJETIVOS 
• Recordar las diferentes fórmulas para determinar áreas de regiones planas. 
• Aplicar adecuadamente las propiedades para determinar áreas de regiones sombreadas. 

ÁREA DE REGIONES PLANAS 
El área es la medida de la extensión de una superficie, expresada en unidades cuadradas.
PROBLEMAS RESUELTOS
PREGUNTA 1 : 
Dada la gráfica ¿Qué fracción representan los cuadrados sombreados? 
A) 3/4 
B) 1/4 
C) 1/12 
D) 1/3 
E) 3/7 
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 2 : 
En el siguiente cuadrilátero, ¿qué parte del total está sombreado? 
A) 5/16 
B) 5/12 
C) 3/16 
D) 3/4 
E) 3/8 
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 3 : 
En la figura se tiene un cuadrado que ha sido dividido en nueve cuadrados congruentes de lado 10cm. ¿Qué fracción del área del cuadrado representa el área de la región sombreada? 
A) 3/4 
B) 2/9 
C) 5/9 
D) 1/9 
E) 7/9
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 4 : 
En la figura se tiene nueve cuadraditos congruentes. Si el lado del cuadrado grande mide 3cm. Halle la relación entre el área de la región sombreada y el área de la región no sombreada. 
A) 4/13 
B) 6/13 
C) 5/13 
D) 2/13 
E) 3/13 
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 5 : 
Si el área total de la figura (II) es los 3/4 del área de la figura (I), ¿qué parte representa el área de la región sombreada de (I) respecto de la región sombreada de (II)? (I) (II) 
A) 2/5 
B) 2/3 
C) 3/4 
D) 2/7 
E) 3/5 
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 6 : 
En el gráfico, ABCD es un rectángulo donde AB=3 y BC=4. Calcula el área de la región sombreada.
A) 13,5
B) 14,5 
C) 15,5 
D) 16,5 
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 7 : 
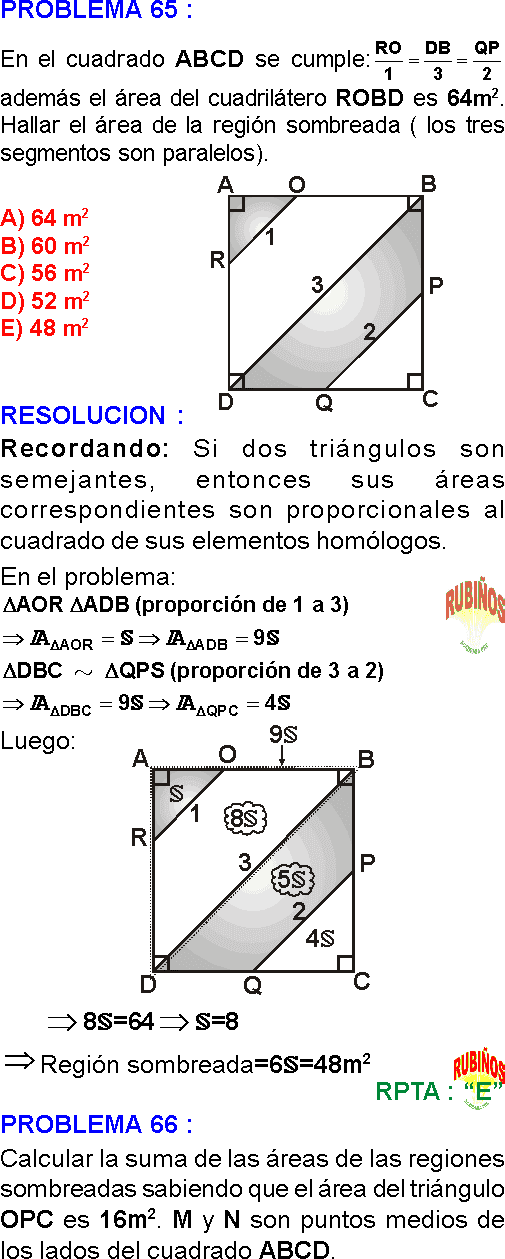
En un cuadrado ABCD, se toman los puntos medios M y N, de CD y AD, respectivamente; los segmentos BM y CN se intersecan en P. Halle el área del cuadrado si el área del triángulo PCM es 2m². 
A) 46 
B) 24 
C) 32 
D) 40 
E) 38 
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 8 : 
Si un círculo completo tiene de área 3A/4 u², calcule la diferencia entre la suma de las áreas de las regiones sombreadas de las dos primeras figuras con el área de la región sombreada de la tercera figura. 
A) 5A/24 u²   
B) 5A/32 u²       
C) 3A/26 u²    
D) 3A/32 u²
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 9 : 
En el gráfico, el perímetro de la región sombreada es (24+3𝛑). Calcula el área de su región si ABCD es un rectángulo. 
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 10 : 
En la figura, el lado del cuadrado ABCD mide 4cm. Calcule la suma de las áreas de las regiones sombreadas en cm². 
A) 4(𝛑 – 3) 
B) (4𝛑 – 3) 
C) 2(𝛑 – 1) 
D) 2(𝛑 – 2) 
E) 4(𝛑 – 2) 
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 11 : 
El radio del cuadrante mide 4√2cm. 
Calcula el área de la región sombreada (en cm²). 
A) 4π – 4 
B) 4π – 8 
C) 4π – 6 
D) 3π – 8 
E) 5π – 6 
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 12 : 
Calcule el área de la región sombreada si “O” y “O1” son centros. Si AB =2u , EF=1u 
A) (√2 – 𝛑/6) u²
B) (√7 – 𝛑/3) u²
C) (√2 – 𝛑/5)/5 u²
D) (√3 – 𝛑/6)/4 u²
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 13 :
Del gráfico, calcule el área sombreada, si PQ=2, R=√2 (T: punto de tangencia). 
A) 2√2 – 2 – 𝛑/2
B) 2√2 – 1 – 𝛑/2
C) 2√2 + 1 – 𝛑/2
D) 2√2 – 1 – 𝛑/2 
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 14 : 
En el gráfico, calcula el área de la región sombreada. 
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 15 : 
En el gráfico mostrado ABCD es un cuadrado ABCD, calcule el área de la región sombreada 
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 16 : 
La figura ABCDEF es un hexágono regular y el área sombreada mide 16√3m² , el perímetro del hexágono es: 
A) 6√3m 
B) 18m 
C) 4√5m 
D) 48m 
E) 16√5 m 
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 17 : 
Del gráfico, O y O1 son centros; A, B, C, D y E son puntos de tangencia. Calcule el área de la región sombreada. 
A) 12√2 u² 
B) 18√2 u² 
C) 22√2 u²
D) 24√2 u² 
RESOLUCIÓN :
Rpta. : "D"
PRACTICA
PREGUNTA 1 :
Calcule el área de una región triangular cuyos lados miden 4 ; 8 y 6. 
A) 4√19 
B) 4√17 
C) 3√15 
D) 5√3 
E) 3√11 
Rpta. : "C"
PREGUNTA 2 :
Las diagonales de una región cuadrangular convexa miden 7 y 8, y determinan un ángulo de 30°. Calcule el área de dicha región. 
A) 12 u2
B) 14 u2 
C) 15 u2
D) 16 u2
E) 18 u2 
Rpta. : "B"
PREGUNTA 3 :
En un triángulo, dos de sus lados miden 10 y 14 m respectivamente y forman un ángulo de 45º. Calcule el área de la región triangular. 
A) 35√7 m2 
B) 18√7 m2 
C) 20√7 m2 
D) 3√2 m2
E) 3√11 m2 
Rpta. : "A"
PREGUNTA 4 :
En una región romboide dos de sus lados miden 10 y 7, y una de sus alturas mide 9. Calcule el área de dicha región. 
A) 64 u2 
B) 57 u2 
C) 63 u2 
D) 54 u2
E) 36 u2 
Rpta. : "C"
PREGUNTA 5 :
Calcule el área de una región triangular cuyos lados miden 5 ; 6 y 7. 
A) 6√6 u2 
B) 2√5 u2 
C) 4√6 u2 
D) 3√2 u2
E) 2√6 u2 
Rpta. : "C"
PREGUNTA 6 :
En una región rombal ABCD de perímetro 52 la diagonal AC mide 24. Calcule el área de dicha región. 
A) 130 
B) 150 
C) 100 
D) 140 
E) 120 
Rpta. : "E"
PREGUNTA 7 :
En un triángulo rectángulo, el cateto menor mide 5 m y la mediana relativa a la hipotenusa mide 6,5 m. Calcule el área de la región triangular. 
A) 24 m2 
B) 42 m2 
C) 48 m2 
D) 30 m2
E) 36 m2 
Rpta. : "D"
PREGUNTA 8 :
En una región romboidal dos de sus lados miden 12 y 9, y una de sus alturas mide 10. Calcule el área de dicha región. 
A) 100 
B) 120 
C) 90 
D) 110 
E) 80 
Rpta. : "C"
PREGUNTA 9 :
Dado un triángulo ABC, obtuso en B, por M, punto medio de AC, se traza hacia BC la perpendicular MN. Si AB = 10 m, BN = 1 m y NC = 7 m, halle el área de la región triangular ABC. 
A) 24 m2 
B) 48 m2 
C) 18 m2 
D) 32 m2
E) 28 m2 
Rpta. : "D"
PREGUNTA 10 :
Dado un cuadrado ABCD de 24 cm de lado, se prolonga AB una longitud BE=6 cm y desde E se traza EF (F en AD), la cual divide al cuadrado en dos cuadriláteros de igual área. Calcule DF. 
A) 4 cm 
B) 6 cm 
C) 5 cm 
D) 8 cm 
E) 3 cm 
Rpta. : "A"
PREGUNTA 11 :
En un triángulo ABC, recto en B, de incentro I, se sabe que IA = 10 u e IC = 8 2 u, calcule el área de la región triangular AIC. 
A) 40 u2 
B) 36 u2 
C) 50 u2 
D) 42 u2
E) 24 u2 
Rpta. : "A"
PREGUNTA 12 :
El largo de un terreno rectangular es el doble del ancho. Si el largo se aumenta en 40 m y el ancho en 6 m, el área se duplica. Calcule el perímetro del terreno original. 
A) 180 m 
B) 120 m 
C) 240 m 
D) 144 m 
E) 160 m 
Rpta. : "A"
PREGUNTA 13 :
En un triángulo isósceles, la base mide 15 m y la altura relativa a uno de los lados iguales mide 12 m. Halle el área de la región triangular. 
A) 75 m2 
B) 47 m2 
C) 55 m2 
D) 65 m2 
E) 45 m2 
Rpta. : "A"
PREGUNTA 14 :
Si se disminuyera el largo de cierto rectángulo en 4 cm y se incrementara el ancho en 3 cm, resultaría un cuadrado con la misma área que el rectángulo original. Halle el perímetro, en cm, del rectángulo original. 
A) 144 cm 
B) 126 cm 
C) 145 cm 
D) 128 cm 
E) 148 cm 
Rpta. : "A"
PREGUNTA 15 :
Un triángulo acutángulo ABC se encuentra inscrito en una circunferencia de centro O, cuyo radio mide 15. Luego, se trazan las alturas AF y CE. Si BA = 3BF y AC=24, calcule el área de la región cuadrangular OEBF. 
A) 45 u2 
B) 37,5 u2 
C) 60 u2
D) 75 u2 
E) 90 u2
Rpta. : "C"
ÁREAS EN DIFERENTES CAMPOS 
El problema de cómo calcular el área de una región determinada tiene sus inicios en la antigüedad, en aquellas civilizaciones donde la base económica era la agricultura. Por ejemplo, surge la necesidad de medir los terrenos de cultivo que, debido a la geografía y otros factores, eran limitadas por diversas figuras geométricas, sabiendo que la experiencia diaria puede dar origen a algunos conceptos sencillos, como la recta, plano y circunferencia. El conocer las propiedades de dichas figuras requiere de estudio, análisis e investigación que el hombre fue desarrollando en el transcurso del tiempo. Prueba de ello, tenemos los restos arquitectónicos dejados por las diferentes culturas que nos muestran su conocimiento sobre las figuras geométricas y sus propiedades. 
Saber calcular el área de una región, tiene aplicación en las actividades prácticas de la vida cotidiana, y actualmente, para construir un edificio o una vivienda es necesario saber cuánto mide el terreno, o en el campo bélico, por ejemplo, para saber qué área será afectada por una explosión.

Ejercicios resueltos de examen de admisión a la Universidad