ÁNGULOS EN LA CIRCUNFERENCIA EJERCICIOS RESUELTOS PDF

APRENDIZAJES ESPERADOS

☛ Reconocer y aplicar la propiedad de los ángulos asociados a la circunferencia.

☛ Emplear de forma correcta los teoremas que se dan en la circunferencia.

La circunferencia dentro de la matemática es vista en la Trigonometría cuando se estudia a la circunferencia trigonométrica, en Geometría Analítica cuando analizamos su ecuación, en Razonamiento Matemático se relaciona con los ordenamientos circulares y en Física se asocia con la fuerza centrípeta y centrífuga.

CIRCUNFERENCIA

Es una línea curva cerrada donde todos sus puntos están a igual distancia de otro punto fijo llamado centro. A dicha distancia se le llama radio.

La circunferencia es una línea, su medida en grados sexagesimales es 360°.

SEMI-CIRCUNFERENCIA

Es la mitad de una circunferencia y en ella, todos los ángulos inscritos son rectos

La medida de una media circunferencia o semicircunferencia es la mitad de la medida de la circunferencia, es decir, 180°.

ÁNGULOS ASOCIADOS A LA CIRCUNFERENCIA

ÁNGULO CENTRAL

Es aquel ángulo que tiene su vértice en el centro de la circunferencia, sus lados contienen cada uno un radio y su medida es igual al arco comprendido entre sus lados; siempre y cuando esta medida del arco sea angular.

El vértice se encuentra en el centro de la circunferencia, sus lados son dos radios.

La medida del ángulo central y su respectivo arco, son iguales.

Siempre que tengas un ángulo central recuerda que al trazar la cuerda que une los puntos de intersección de esta con la circunferencia

ÁNGULO INSCRITO

Su vértice se encuentra sobre la circunferencia y sus lados son dos cuerdas.

La medida del ángulo inscrito es igual a la mitad de la medida del arco comprendido entre sus lados.

La medida del arco es el doble de la medida de su respectivo ángulo inscrito.

ÁNGULO INTERIOR

Su vértice se encuentra en el interior de la circunferencia, está formado por dos secantes que contienen dos cuerdas que se cortan y su medida es igual a la semi suma de los arcos interceptados por él y por su opuesto por el vértice.

ÁNGULO EXTERIOR

Su vértice se encuentra en el exterior de la circunferencia, pudiendo ser sus lados dos secantes, una secante y una tangente o dos tangentes.

ÁNGULO SEMI INSCRITO

El vértice se encuentra sobre la circunferencia y sus lados son una tangente y una cuerda.

La medida del ángulo seminscrito es igual a la mitad del arco correspondiente a la cuerda.

La medida del ángulo semi inscrito , se determina con una recta tangente y una recta secante que pasa por dicho punto de tangencia.

ANGULO EXINSCRITO

Su vértice se encuentra sobre la circunferencia, este ángulo es el adyacente suplementario de un ángulo inscrito.

Es el suplemento de un ángulo inscrito, su vértice se encuentra en la circunferencia, un lado contiene una cuerda y el otro lado la parte exterior de una secante y su medida es igual a la mitad de la medida de todo el arco que no corresponde al ángulo inscrito.

CUADRANTE

Es la cuarta parte de una circunferencia y en ella los ángulos exinscritos miden 45°.

PROBLEMAS RESUELTOS

PREGUNTA 1 :

Un trapecio isósceles se encuentra inscrito en una circunferencia. Si la diferencia de los arcos de las bases es 160°, calcular uno de los ángulos agudos.

A) 30°

B) 50°

C) 70°

D) 80°

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 2 :

En la figura adjunta, ABC es un triángulo equilátero y α es 100°. Halle el valor de β

A)10°

B) 20°

C) 40°

D) 30°

E) 15°

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 3 :

En la figura, O es centro de la circunferencia, OM = SN. Halle x.

A) 17°

B) 14°

C) 15°

D) 13°

E) 16°

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 4 :

Un cuadrilátero inscrito en una circunferencia tiene tres lados iguales, cada uno de los cuales subtiende un arco de 60°. Halle la suma de las medidas del mayor y menor ángulo interno del cuadrilátero.

A) 240°

B) 180°

C) 160°

D) 150°

E) 210°

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 5 :

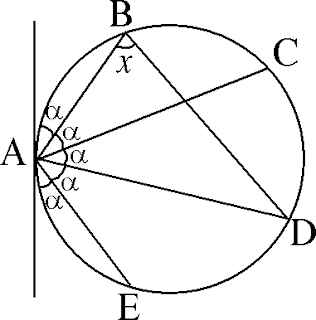
Mario dibuja cinco puntos, A, B, C, D y E, en una circunferencia, así como la recta tangente a la circunferencia en A, como se muestra en la figura, de tal manera que los cinco ángulos marcados con a son congruentes. Halle el valor de x.

A) 36°

B) 45°

C) 53°

D) 72°

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 6 :

Se tiene una semicircunferencia de centro O, calcula “x” (T; P: puntos de tangencia).

A) 37°

B) 53°

C) 30°

D) 45°

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 7 :

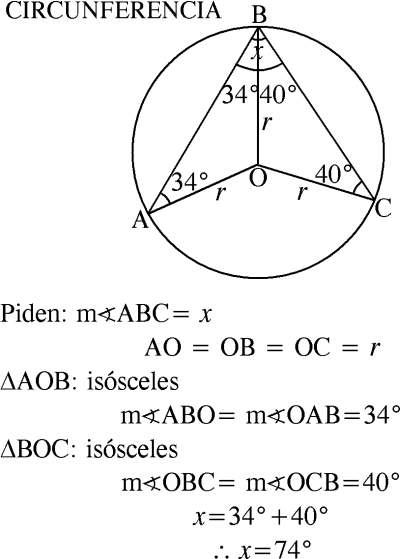
En la clase de Geometría, el profesor indica la importancia de la circunferencia en diferentes aspectos de la vida diaria; para ello utiliza un transportador que, como sabemos, nos sirve para medir ángulos o dibujar circunferencias, tal como se muestra en la figura. Si el punto O es centro de la circunferencia, ¿cuál es la medida del ángulo ∠ABC?