VALOR POSICIONAL DE UN DECIMAL EJEMPLOS RESUELTOS PDF
VALOR DE POSICIÓN DE LAS CIFRAS DE UN NÚMERO DECIMAL
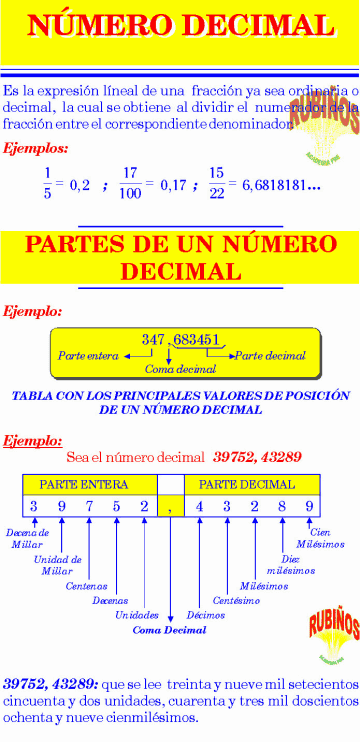
Así como en la parte entera cada posición de las cifras se enuncia como unidades, decenas, etc. en la parte decimal tenemos
A un número decimal se le puede agregar ceros a la derecha y el valor no se altera.
Ejemplo :
8,25 = 8,250000
Explica cómo usar una tabla de valor posicional para mostrar el valor de cada uno de los dígitos o cifras de un número decimal hasta las cien milésimas.
Explica cómo puedes usar patrones cuando se usa el valor posicional para comprender decimales.
También puedes usar una tabla de valor posicional para hallar el valor de cada uno de los dígitos de un decimal.
El valor de cada lugar de un decimal equivale a diez veces el valor del lugar que está a su derecha.
Estimar o hallar una respuesta exacta comprender los decimales
La idea importante
Los valores posicionales que están a la derecha de la coma decimal en el sistema de base diez nombran los números menores que uno.
Investiga
Quieres comprar un computador nuevo.


.gif)
.gif)
.gif)


