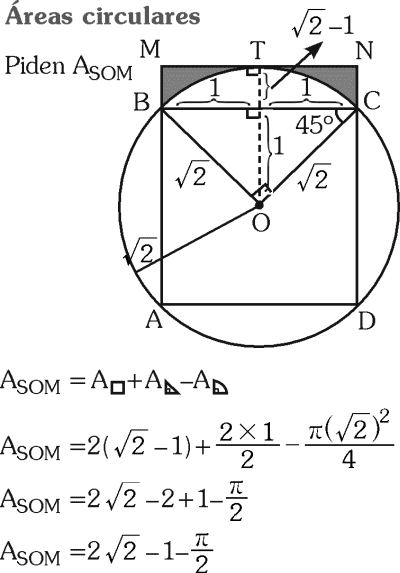GEOMETRÍA SIMULACRO BECA 18 PRUEBA ÚNICA NACIONAL DEL PRONABEC DESARROLLADA EXAMEN DE INGRESO UNIVERSIDAD RESUELTA PRIMERA OPCIÓN POP EVALUACIÓN DE TALENTO PUCP

PREGUNTA 21

El suplemento de un ángulo más el complemento de otro ángulo es 140°. Calcula el suplemento de la suma de los dos ángulos.

A) 20°

B) 30°

C) 40°

D) 50°

Resolución

Rpta. : "D"

PREGUNTA 22

Un trapecio isósceles se encuentra inscrito en una circunferencia. Si la diferencia de los arcos de las bases es 160°, calcular uno de los ángulos agudos.

A) 30°

B) 50°

C) 70°

D) 80°

Resolución

Rpta. : "B"

PREGUNTA 23

En un triángulo rectángulo ABC (recto en B) se inscribe el cuadrado PQRS (PS en el segmento AC), si AP=50 y SC=72. Calcula el lado del cuadrado.

A) 40

B) 50

C) 60

D) 70

Resolución

Rpta. : "C"

PREGUNTA 24

En un triángulo rectángulo ABC se traza la altura BH y la mediana BM, si m∠C=20°. Calcula m∠HBM.

A) 40°

B) 60°

C) 50°

D) 70°

Resolución

Rpta. : "C"

PREGUNTA 25

Una esfera de 100𝛑m² de área está inscrita en un cilindro. Calcular el volumen del cilindro.

A) 200𝛑m³

B) 220𝛑m³

C) 250𝛑m³

D) 260𝛑m³

Resolución

Rpta. : "C"

PREGUNTA 26

Cinco ángulos consecutivos en progresión aritmética forman un ángulo llano. Si el mayor es el cuadrado del menor, calcular la medida del menor ángulo.

A) 4

B) 8

C) 6

D) 10

Resolución

Rpta. : "B"

PREGUNTA 27

Un ∆ ABC tiene por coordenadas A(–5;1) , B(–5;4) y C(2;4). Calcular el área del triángulo.

A) 10,5 u²

B) 12,5 u²

C) 14,5 u²

D) 16 u²

Resolución

Rpta. : "A"

PREGUNTA 28

Colocando cinco cubos verticalmente, se determina un prisma de diagonal 18; calcula el área total del prisma.

A) 216 u²

B) 172 u²

C) 241 u²

D) 264 u²

Resolución

Rpta. : "A"

PREGUNTA 29

En el cuadrado, ABCD la suma de las áreas de los triángulos rectángulos isósceles sombreados es la cuarta parte del área del cuadrado; calcula “x”.

Resolución

Rpta. : "D"

PREGUNTA 30

En un triángulo rectángulo ABC, recto en B, la altura relativa a la hipotenusa mide √24 y determina dos segmentos proporcionales a 2 y 3. Calcula el cateto BC.

A) 4√2

B) 2√15

C) 7√5

D) 9√3

Resolución

Rpta. : "B"

PREGUNTA 31

Si ABCD es un rectángulo inscrito en la semicircunferencia de radio igual a 2 cm, calcula el área de la región sombreada. (“θ” está en radianes).

A) 2θ–sen2θ

B) 4θ–5senθ

C) 5θ–2senθ

D) 3θ–4senθ

Resolución

Rpta. : "A"

PREGUNTA 32

Se tiene una propiedad en litigio por 3 hermanos. Llega un perito y soluciona el problema dividiendo la propiedad en 3 regiones triangulares. Supongamos que la propiedad es un triángulo ABC en el cual se traza la ceviana AR (R en BC), se toma un punto S en AR. Si AR=3(AS) y RC=4(BR), calcula la mayor área de los triángulos divididos. El área total de la propiedad es de 60 hectáreas.

A) 24 hectáreas

B) 12 hectáreas

C) 48 hectáreas

D) 36 hectáreas

Resolución

Rpta. : "C"

PREGUNTA 33

En un triángulo rectángulo, el producto de catetos es 120 y la suma de dichos catetos es 23. Calcula la longitud de la hipotenusa.

A) 15

B) 13

C) 12

D) 17

Resolución

Rpta. : "D"

PREGUNTA 34

En un rectángulo ABCD se hace coincidir el vértice B con D, tal como se muestra en la figura. Si BC= 20 cm y AB= 10 cm, calcula PC.

A) 6,5

B) 7

C) 7,5

D) 8

Resolución

Rpta. : "C"

PREGUNTA 35

A) 52º30’

B) 56º15’

C) 58º20’

D) 60º21’

Resolución

Rpta. : "B"

PREGUNTA 36

En un triángulo ABC, AB= 25, m∠A= 106º y m∠B= 37º. Calcula el área del triángulo ABC.

A) 150 m²

B) 200 m²

C) 250 m²

D) 300 m²

Resolución

Rpta. : "D"

PREGUNTA 37

A) 20

B) 30

C) 40

D) 50

Resolución

Rpta. : "B"

PREGUNTA 38

Del gráfico, AEFD es un cuadrado, ABCD es un rectángulo, M es punto medio y AM = 1. Calcule el área de la región EBCF.

A) 4 u²

B) 6 u²

C) 8 u²

D) 10 u²

Resolución

Rpta. : "C"

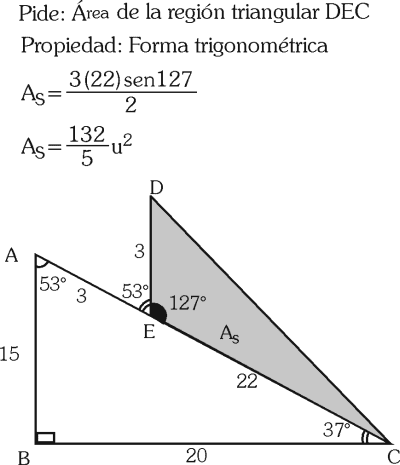
PREGUNTA 39

A) 120/7 u²

B) 132/5 u²

C) 140/9 u²

D) 135/8 u²

Resolución

Rpta. : "B"

PREGUNTA 40

Del gráfico, O y O₁ son centros; A, B, C, D y E son puntos de tangencia. Calcule el área de la región sombreada.

A) 12√2 u²

B) 18√2 u²

C) 22√2 u²

D) 24√2 u²

Resolución

Rpta. : "D"

PREGUNTA 41

A) √5 – √(14/3)

B) √5 – √5/3

C) √7 – √(14/3)

D) √6 – √(14/3)

Resolución

Rpta. : "C"

PREGUNTA 42

En el gráfico, AB=BL=LP=PC y AD=DL=LQ=QC. Calcule: x+y

A) 50º

B) 30º

C) 40º

D) 60º

Resolución

Rpta. : "B"

PREGUNTA 43

En un triángulo rectángulo ABC se prolonga la hipotenusa hasta un punto D.

Si BC=CD=7 y AD=32, calcule la altura relativa a la hipotenusa.

A) 6,25

B) 6,72

C) 5,12

D) 5,25

Resolución

Rpta. : "B"

PREGUNTA 44

Se tienen dos triángulos equiláteros, uno inscrito y el otro circunscrito a una misma circunferencia. Si el área de la región determinada por las dos regiones triangulares es 9√3 u², calcule la longitud de la circunferencia.

A) 3𝛑

B) 2𝛑

C) 4𝛑

D) 6𝛑

Resolución

Rpta. : "C"

PREGUNTA 45

Se tienen dos circunferencias circunscritas a dos hexágonos regulares. Si sus radios miden 4 y 8, calcule la relación de áreas de las regiones determinadas entre las circunferencias y sus polígonos regulares inscritos.

A) 1/4

B) 1/2

C) 1/8

D) 1/6

Resolución

Rpta. : "A"

PREGUNTA 46

Del gráfico, calcule el área sombreada, si PQ=2, R=√2 (T: punto de tangencia).

A) 2√2 – 2 – 𝛑/2

B) 2√2 – 1 – 𝛑/2

C) 2√2 + 1 – 𝛑/2

D) 2√2 – 1 – 𝛑/2

Resolución

Rpta. : "D"

PREGUNTA 47

Del gráfico; el diámetro, AC mide 32μ, BO=4. Si FB⊥AC, calcule el perímetro de la región triangular AFC.

A) 4√6 + 5√10 + 32

B) 8√6 + 7√10 + 32

C) 8√6 + 8√10 + 32

D) 5√3 + 7√8 + 36

Resolución

Rpta. : "C"

PREGUNTA 48

Calcule el área de la región sombreada si “O” y “O1” son centros. Si AB = 2u , EF = 1u

A) (√2 – 𝛑/6) u²

B) (√7 – 𝛑/3) u²

C) (√2 – 𝛑/5)/5 u²

D) (√3 – 𝛑/6)/4 u²

Resolución

Rpta. : "D"

PREGUNTA 49

En una circunferencia de radio cuatro, se inscribe un cuadrado, luego se construye exteriormente los triángulos equiláteros formándose un octógono del cual nos piden el área.

A) 32(√3 + 1)

B) 32(√2 + 1)

C) 16(√2 + 1)

D) 32(√5 + 1)

Resolución

Rpta. : "A"

PREGUNTA 50

En un triángulo isósceles de base AC=1, se trazan las medianas que parten de los extremos de las bases y son perpendiculares. Calcula el área de la región triangular.

A) 1/2

B) 1/3

C) 1/4

D) 3/4

Resolución