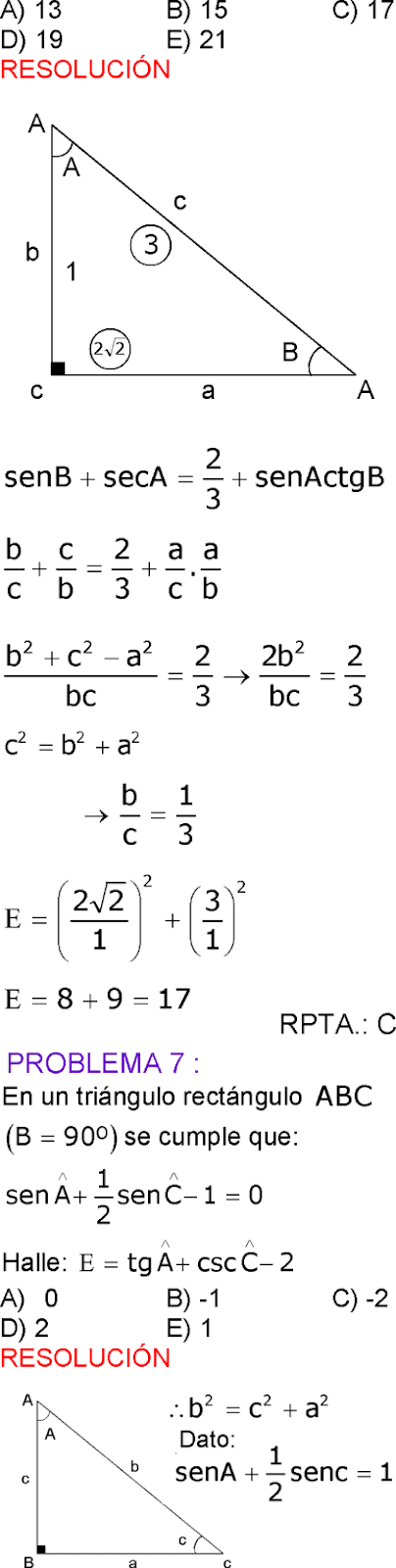SENO COSENO TANGENTE COTANGENTE SECANTE COSECANTE EJERCICIOS RESUELTOS PDF
OBJETIVOS :
• Conocer correctamente las definiciones de las razones trigonométricas de un ángulo agudo.
• Calcular las razones trigonométricas de un ángulo agudo a partir del triángulo rectángulo en que se encuentre.
• Conocer el cálculo de las razones trigonométricas de un ángulo agudo.
• Determinar las razones trigonométricas de ángulos que miden 30°; 60°; 45°; 37° y 53°, y la relación que existe entre sus lados aplicando la definición.
• Aplicar las propiedades que cumplen las razones trigonométricas para simplificar las expresiones.
• Utilizar los conceptos vertidos en el presente capítulo en situaciones cotidianas.
Para el estudio de las razones trigonométricas es necesario conocer a los ángulos, que son elementos geométricos que en nuestro curso tiene una serie de consideraciones especiales, por lo que se estudia previamente una teoría angular enfocada desde el punto de vista de la trigonometría que nos permitirá aprender la importancia del ángulo radian como unidad angular del sistema radial y el triángulo rectángulo que es un elemento muy importante dentro de la trigonometría, ya que en este triángulo podemos definir las razones trigonométricas (seno, coseno, tangente, cotangente, secante y cosecante) que son muy utilizadas en los campos de la topografía, astronomía, física, etc.).
El estudio del presente capítulo permite entender los conceptos matemáticos que han sido utilizados en las construcciones hechas desde la Antigüedad, en las que se usa la medida del ángulo.
RAZÓN
En términos generales, es la comparación de dos cantidades.
Para las longitudes de los lados de un triángulo, esta comparación se determina mediante su cociente.
RAZONES TRIGONOMÉTRICAS
Es el cociente que se establece de dos valores de sus lados con respecto a uno de sus ángulos agudos.
Las razones trigonométricas son seis y se denominan: seno, coseno, tangente, cotangente, secante y cosecante ; su notación es la siguiente:
• senA : seno del ángulo A o seno de A
• cosA : coseno del ángulo A o coseno de A
• tanA : tangente del ángulo A o tangente de A
• cotA : cotangente del ángulo A o cotangente de A
• secA : secante del ángulo A o secante de A
• cscA : cosecante del ángulo A o cosecante de A
POSICIÓN RELATIVA DE CATETOS
Los catetos de un triángulo rectángulo pueden denominarse tanto opuestos como adyacentes respecto a un ángulo dependiendo de su posición relativa.
☞ En un triángulo, a mayor ángulo se le opone un mayor lado
☞ En todo triángulo rectángulo la longitud de la hipotenusa es mayor que la longitud de tos catetos,
☞ En todo triángulo rectángulo el cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de las longitudes de los catetos, (Teorema de Pitágoras).
☞ Si conocemos una razón trigonométrica para un ángulo, podemos calcular las demás.
GUIA DE CLASE
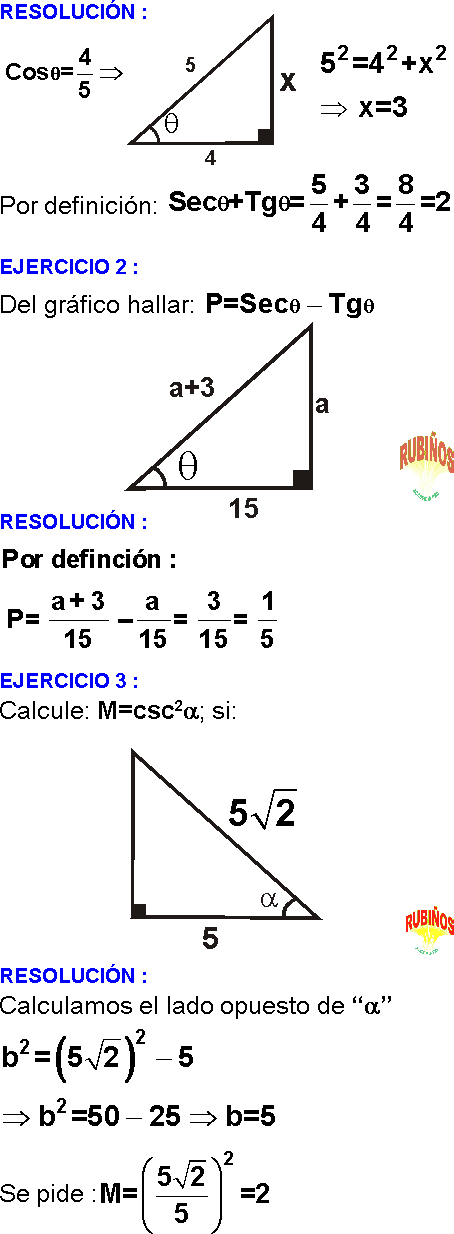
PROBLEMA 1 :
Si : Senβ= 60/61 .
Calcula el valor de :
Tgβ + Secβ
a) 101/11
b) 1/11
c) 11
d) 10
e) 13/11
Rpta. : "C"
PROBLEMA 2 :
El perímetro de un triángulo rectángulo es 338m. Si la tangente de uno de los ángulos agudos es 2,4m ¿Cuánto mide el cateto menor?
a) 13m
b) 33,8m
c) 50m
d) 56,33m
e) 55
Rpta. : "D"
PROBLEMA 3 :
Determina el área de un triángulo rectángulo, si la hipotenusa mide 54 cm, y el coseno del ángulo formado por la altura y la mediana relativa a la hipotenusa es igual a 2/3.
a) 420 cm²
b) 450 cm²
c) 486 cm²
d) 962 cm²
e) 243 cm²
Rpta. : "C"
PROBLEMA 4 :
Los lados de un triángulo rectángulo son números consecutivos. El coseno del mayor ángulo agudo de ese triangulo es:
a) 3/2
b) 3/4
c) 1/2
d) 3/5
e) 4/5
Rpta. : "D"
PROBLEMA 5 :
En el triángulo ABC recto en A, se sabe que ctgC+ctgB=4
Entonces al calcular 16senB.senC.cosB.cosC se obtiene:
A) 1/4
B) 1/2
C) 1
D) 2
E) 4
Rpta. : "C"
PROBLEMA 6 :
En el triángulo ABC recto en B, se verifica
secA + tgA=1/4
Hallar el valor de 6(cscC – ctgC)
A) 36
B) 42
C) 24
D) 30
E) 48
Rpta. : "C"
PROBLEMA 7 :
Siendo β un ángulo agudo
15senβ – 8cosβ = 0
Calcule 0,5senβ + 2cosβ
A) 1
B) 2
C) 3
D) 4
E) 5
PROBLEMA 8 :
Si tgθ = 1/2; θ = agudo
Calcule sen²θ – cos²θ
A) 3/4
B) 4/5
C) –3/5
D) –4/5
E) 1/5
PROBLEMA 9 :
En un triángulo rectángulo ABC recto en B reducir:
(secA – senC)ctgA – cosC
a) 1
b) 2
c) 0
d) 3
e) – 1
PROBLEMA 10 :
En un triángulo ABC recto en C simplificar:
actgA – csenB
a) 0
b) 1/3
c) a
d) b
e) 1/2
PROBLEMA 11 :
Se tiene un triángulo rectángulo ABC (m∢A=90°).
Calcular : btgC + ctgB – c
a) a
b) b
c) c
d) 2a
e) 2c
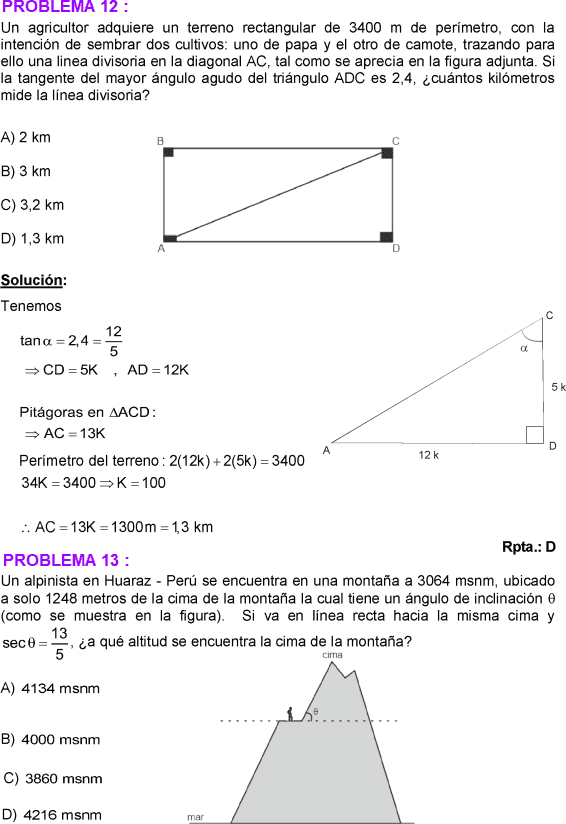
PROBLEMA 12 :
En un triángulo ABC recto en A se cumple tgB = 0,75; además: a – b = 6 m
Hallar su perímetro.
a) 12 m
b) 24 m
c) 36 m
d) 42 m
e) 45 m
PROBLEMA 13 :
Lenin camina por una rampa dándose cuenta que por cada 1,5cm que avanza en forma horizontal sube 1m. Calcular la tangente del ángulo que forma la rampa con la horizontal.
PROBLEMA 14 :
Vlady caminando por una rampa se dio cuenta, que por cada 2m que sube, avanza 3,5m. en forma horizontal. Calcular la tangente del ángulo que forma la rampa con la horizontal.
PROBLEMA 15 :
Caminando por una rampa Edu se da cuenta, que por cada 1m. que sube, avanza horizontalmente 2m. Calcular la tangente del ángulo que forma la rampa con la horizontal.
OBJETIVOS FINALES QUE DEBES OBTENER :
☛ Aplicar el Teorema de Pitágoras.
☛ Identificar los elementos para definir una razón trigonométrica.
☛ Definir una razón trigonométrica.
☛ Definir las razones trigonométricas: ctg, sec, csc.
☛ Calcular las R.T. de un ángulo, conocida una de ellas.
☛ Interpretar enunciados de características geométricas.
☛ Identificar la proporción en que se encuentran los lados de un triángulo rectángulo notable.
☛ Reconocer el valor numérico de las razones trigonométricas de ángulos notables y aproximados.
☛ Resolver triángulos rectángulos, relacionando las longitudes de los lados mediante una razón trigonométrica.
☛ Encontrar equivalencias entre las razones trigonométricas de ángulos notables en enunciados de características geométricas.
EL TEOREMA DE PITÁGORAS EN LA TRIGONOMETRÍA
En el antiguo Egipto existían los llamados «TENSORES DE CUERDAS» llamados harpedonaptas, los cuales aprovechaban para formar ángulos rectos, una propiedad del triángulo rectángulo.
Usando muchos señalaban en una cuerda trozos proporcionales a los números 3, 4 y 5, la cuerda la ponían bien tensa, sujeta por dos estacas y juntaban los extremos. El resultado era una escuadra llamada «TRIÁNGULO EGIPCIO» que servía a los constructores de templos.
Pitágoras de Samos, que conoció esta cuerda, «experimento» las relaciones entre los valores numéricos 3, 4 y 5 descubriendo su famoso teorema al comprobar que el cuadrado de 5 era igual a la suma de los cuadrados de 3 y 4. El importantísimo teorema descubierto por Pitágoras, el cual se le llamó REGLA DE ORO DE LA GEOMETRÍA, fue demostrado dos siglos después de Euclides.
La más conocida e intuitiva de las demás demostraciones es la del matemático hindú Bhaskara hace más de ocho siglos y medio.
Una aplicación del teorema de Pitágoras nos lleva a la famosa relación trigonométrica.
ORIGEN DEL TÉRMINO TANGENTE
La relación entre la altura de un poste y la longitud de su sombra, existía en la mente de los antiguos matemáticos.
Así para medir el paso del tiempo inventaron el reloj de sol de dos tipos: uno con la varilla vertical de modo que su sombra se proyectará sobre una superficie horizontal; el otro tipo con su varilla inclinada y sujeta a una pared vertical, de modo que su sombra se proyectaba sobre la pared. No fue sino en el siglo X d.n.e. cuando los árabes empezaron a estudiar longitudes análogas relacionados con el radio de una circunferencia.
Tuvieron que pasar otros cinco siglos para que la palabra tangente se le asignará a una recta tal como la indicada por TN (figura).
La tangente a una circunferencia es la recta que la toca en un solo punto (del latín: tango, que significa “toco”).
Supongamos que TN es la parte de la tangente a la circunferencia; ON el radio y OT la prolongación de una recta en movimiento o radio rector. En el siglo XVI los matemáticos empezaron a designar a TN como la tangente del ángulo TN.