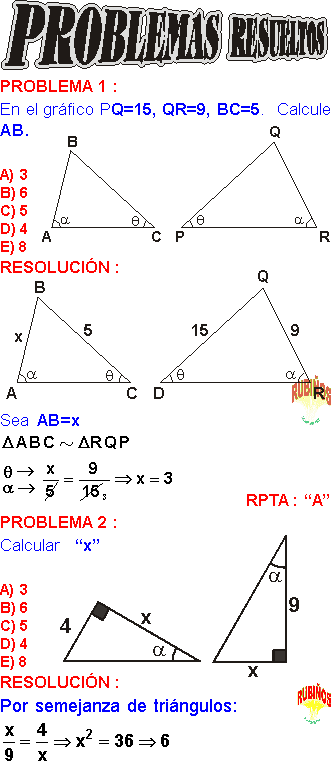
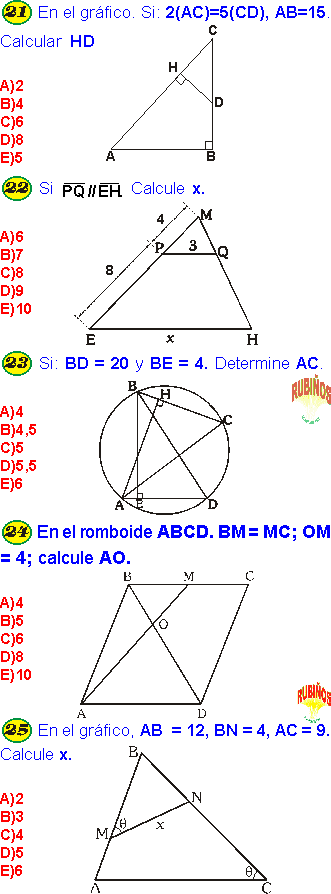
TRIÁNGULOS SEMEJANTES EJERCICIOS RESUELTOS PDF
PROPÓSITO DE LA UNIDAD
La semejanza de figuras planas es un contenido matemático que es trabajado en los distintos niveles
de la Educación Media, debido a su importancia desde el punto de vista matemático y también por
su relevancia en contextos reales.
Durante esta unidad, queremos que los y las estudiantes sean capaces de identificar figuras semejantes, más allá de la simple visualización. Para ello, son enseñados tres importantes criterios de semejanza y el teorema de Thales, con el objeto de que puedan reconocer matemáticamente si diferentes figuras presentadas son semejantes, como por ejemplo al analizar la igualdad de ángulos y la proporcionalidad de los lados correspondientes. Toda esta amplitud y profundización de contenidos tiene como finalidad aplicar los nuevos conocimientos adquiridos en situaciones del contexto real. Por este motivo, a lo largo de la unidad, se presentan diversos problemas de aplicación con el propósito de que los y las estudiantes puedan observar la presencia de los contenidos enseñados en diferentes contextos matemáticos y cotidianos. En esta unidad se introduce en concepto de semejanza. Intuitivamente, las figuras semejantes están relacionadas por una transformación, ya sea de dilatación o contracción de sus longitudes, de modo que las razones entre las medidas de las distintas rectas que componen la figura original y la dilatada es la misma, así como los ángulos correspondientes. La razón entre sus longitudes es una medida de la magnificación de la transformación. Un caso especial de esto es la congruencia, donde la magnificación es igual a 1. Dos figuras que cumplan lo anterior, pero que estén rotadas una con respecto a otra, pueden causar cierta dificultad. Para ello, debe hacerse hincapié en la definición. Por ejemplo, dos figuras pueden ser semejantes pero no estar “semejantemente ubicadas”, tal como se muestra en la figura de la cámara oscura. Actividades complementarias 1. Supón que dos triángulos cumplen que la razón entre sus correspondientes lados es constante, ¿se puede decir que los triángulos son semejantes?, ¿es necesario verificar también que los ángulos correspondiente son iguales, tal como se enuncia en la definición del Texto? 2. Discute con tus compañeros y compañeras acerca de cómo se podría definir semejanza, en general, para figuras que no están formadas por segmentos de rectas. ¿Qué puedes decir de las figuras mostradas en la siguiente figura? En esta sección, se demuestra el teorema de Thales y su recíproco. Debe quedar claro que el recíproco establece condiciones para que dos rectas que cortan a dos secantes sean paralelas. De este modo, se pueden plantear condiciones sobre los segmentos proporcionales (según el teorema), aun cuando sus medidas son desconocidas. Por ejemplo, un tipo de problema muy común es que al alumno o alumna se le pregunta “¿qué valor debe tener x (algún segmento a determinar en el problema) para que las rectas sean paralelas?” El concepto de homotecia de razón negativa puede ser difícil de visualizar y entender para sus estudiantes. Para aclararles esto, puede dibujar en el pizarrón algunos ejemplos, poniendo énfasis en cómo se invierte la orientación de los distintos segmentos que componen una figura. También puede ser difícil visualizar una homotecia cuando el centro de la homotecia está dentro de la figura dada, tal como se plantea el problema 2. Puede aclarar este punto haciendo notar que el concepto de homotecia como una transformación de la figura no guarda relación con que el centro de la homotecia se encuentre en algún lugar particular del plano, ya que la forma de construir la imagen de una figura bajo una homotecia es siempre la misma. Semejanza de figuras ANALICEMOS... La imagen muestra la letra A tal como se ve cuando se pega, como imagen, en un editor de texto, como el Word. Cuando se quiere modificar esta imagen, ya sea ampliarla, reducirla o expandirla, se debe arrastrar con el mouse alguno de los puntos en los que aparece la doble flecha. Observa cómo se modifican las imágenes, en cada caso: En la situación anterior, se puede observar que cuando se ubica el cursor en el punto central de uno de los lados y se arrastra, la letra A se expande solo de manera horizontal, y se ve más ancha. De hecho, se deforma, ya que los ángulos del triángulo interno cambian y la proporción entre sus medidas no se mantiene constante. Ahora, si se ubica el cursor en el punto central, de arriba o de abajo y se arrastra, la letra se expande solo de manera vertical, y la letra A aparece alargada. Como en el caso anterior, cambian los ángulos del triángulo interno y la proporción entre sus lados. Finalmente, si se ubica el cursor en el punto ubicado en alguna de las esquinas, y se arrastra en diagonal, la letra A se expande de forma vertical y horizontal simultáneamente, y se mantiene la forma, ya que los ángulos son congruentes y todas las proporciones se conservan. En este caso, diremos que la figura inicial y la resultante son semejantes. • Entre ellas, ¿en qué se parecen?, ¿en qué se diferencian? • Mide los ángulos del triángulo central de cada una de las letras. En cada caso, ¿son iguales a la primera?, ¿por qué? • Mide la longitud de cada parte de la letra. En cada caso, ¿son proporcionales a la primera?, ¿por qué? • ¿Cuál de ellas se parece más a la letra original? Justifica. GLOSARIO propiedad de dos figuras de tener la misma forma y tamaño; cuando al poner una figura sobre la otra, ambas coinciden. 147 Unidad 4 • Dos figuras son semejantes si todos sus correspondientes ángulos son congruentes y la razón entre sus correspondientes lados es constante. EN RESUMEN 1. Utiliza un par de escuadras y verifica que solo en el último caso el lado izquierdo de la letra A es paralelo al de la letra original. ¿Sucederá lo mismo para los otros lados de las letras A?, ¿por qué? 2. Dibuja en tu cuaderno dos figuras que sean semejantes. Luego, une los correspondientes puntos de cada letra con una recta. Comprueba que siempre estas rectas se cortan en un solo punto. 3. Explica por qué dos figuras no son semejantes si alguno de sus ángulos no son congruentes.







































.gif)

