SEMEJANZA DE TRIÁNGULOS EJERCICIOS RESUELTOS PDF
PROBLEMAS RESUELTOS
PREGUNTA 1 :
En el lado AC del triángulo ABC se toma el punto D tal que AD= 6, DC= 8. Si la longitud de la perpendicular DH bajada al lado BC es 4, entonces la longitud de la altura del triángulo bajada desde el vértice A al lado BC es:
A) 5
B) 6
C) 7
D) 8
E) 9
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 2 :
En un triángulo acutángulo ABC se trazan las alturas AN y CM, tal que AM=2 u, MB=3 u y BC=6 u. Calcula BN.
A) 2,25 u
B) 2,5 u
C) 2,75 u
D) 3,5 u
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 3 :
En un triángulo de lados 6 y 12 se inscribe un rombo, calcule el lado de dicho rombo.
A) 1
B) 2
C) 3
D) 4
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 4 :
A) 20
B) 30
C) 40
D) 50
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 5 :
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 6 :
De la figura mostrada, MN//BC, AB=4 y BC=6.
Calcula BM.
A) 1,2
B) 1,8
C) 2,4
D) 3
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 7 :
En un romboide ABCD, BC=2AB. La bisectriz de B interseca a la prolongación de CD en Q y la bisectriz de A interseca a BD en M y a BC en P. Si MB=4 cm y PQ=12 cm, halle MD en cm.
A) 9
B) 14
C) 12
D) 10
E) 8
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 8 :
En un cuadrado ABCD, si la intersección entre AC y BM es N; AM=MD y la distancia de N a AM es 20 u.
Calcula el área de la región cuadrada ABCD.
A) 1800 m²
B) 3600 m²
C) 4800 m²
D) 2700 m²
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 9 :
Del gráfico mostrado, calcule CD si AC=24 μ, BC=8 μ y O es centro.
A) √2
B) 2√2
C) 3√2
D) 4√2
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 10 :
En el gráfico, AH=3, AP=2, AL=AM+2; calcule AM.
A) 2,5
B) 3
C) 4
D) 4,5
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 11 :
Del gráfico mostrado, si AB=5 , CD=2 y BC=7, calcule FC.
A) 2,5
B) 1,5
C) 2
D) 3
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 12 :
Del gráfico, BG=15, GL=18, EF=6 y AD=4(DF); calcule AB ( ▱ABCD: paralelogramo). 
A) 9
B) 10
C) 11
D) 12
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 13 :
En la figura adjunta, M, N y P son puntos de tangencia; O y O' son centros de las circunferencias. Si PM= 2PN, halle el valor de r'/r.
A) 3
B) 2
C) 4
D) 6
E) 5
RESOLUCIÓN :
Rpta. : "C"
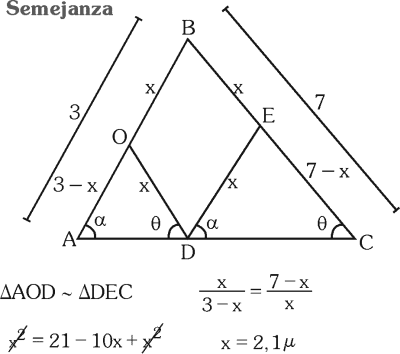
PREGUNTA 14 :
A) 2 μ
B) 2,1 μ
C) 2,5 μ
D) 3 μ
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 15 :
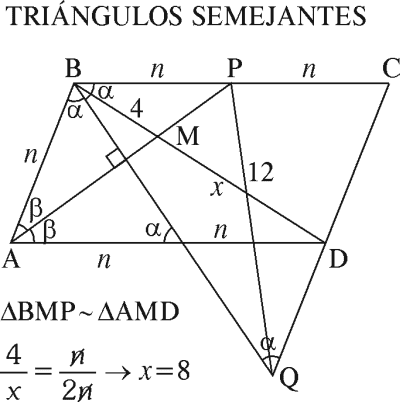
A) 3 μ
B) 4 μ
C) 7 μ
D) 8 μ
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 16 :
En un triángulo rectángulo ABC (recto en B) se inscribe el cuadrado PQRS (PS en el segmento AC), si AP=50 y SC=72. Calcula el lado del cuadrado.
A) 40
B) 50
C) 60
D) 70
RESOLUCIÓN :
Rpta. : "C"
PROBLEMAS PROPUESTOS
PREGUNTA 1 :
Calcular el perímetro de un triángulo si es semejante a otro, de lados: 6; 9 y 10. Además la razón con el primero es 1/5.
a) 5
b) 25
c) 100
d) 125
e) 250
PREGUNTA 2 :
Los lados de un triángulo miden 18; 24 y 36 u. Hallar el menor lado de un triángulo semejante cuyo perímetro es 65 u.
a) 16 u
b) 10
c) 15
d) 20
e) 18
PREGUNTA 3 :
Hallar la longitud de la altura de una torre que forma una sombra de 8 m en el mismo instante que un poste de 5 m produce una sombra de 2 m.
a) 15 m
b) 20
c) 30
d)18
e) 24
PREGUNTA 4 :
Una torre de 15 m de altura proyecta una sombra de 60 m de longitud. ¿Cuál es la estatura de un niño que a la misma hora proyecta una sombra de 4 m de longitud?
a) 1 m
b) 1,2
c) 1,4
d) 1,6
e) 1,8
PREGUNTA 5 :
Se tiene un triángulo rectángulo ABC, recto en “B”, de altura BH igual a 4 y AC = 12. Calcular el lado del cuadrado inscrito, uno de cuyos lados está en la hipotenusa.
a) 3
b) 4
c) 6
d) 2
e) 1
PREGUNTA 6 :
Calcular la altura de un trapecio rectángulo sabiendo que las diagonales son perpendiculares y que las bases miden 12 y 27.
A) 16
B) 12
C) 18
D) 24
E) 18,5
PREGUNTA 7 :
En un triángulo ABC se traza la bisectriz interior BR. Hallar “AR”; si: AB = 6 ; BC = 8 ; RC = 5.
a) 2,75
b) 3
c) 3,5
d) 3,75
e) 4
PREGUNTA 8 :
Las bases de un trapecio miden 4 y 8 y la altura 9, calcule la distancia del punto de intersección de los lados no paralelos a la base mayor.
a) 14
b) 15
c) 16
d) 7
e) 18
PREGUNTA 9 :
En un trapecio ABCD las bases AB y CD están en la relación de 2 a 5 y las diagonales se cortan en “O”. Si la distancia de “O” hacia AB es 2 cm, hallar la altura del trapecio.
a) 6 cm
b) 8
c) 9,5
d) 10,5
e) 7
PREGUNTA 10 :
El lado AC del triángulo ABC se divide en ocho partes iguales, siete segmentos de rectas paralelas a BC se dibujan desde los puntos de división. Si: BC = 10, calcular la suma de las longitudes de los siete segmentos.
a) 36
b) 49
c) 35
d) 42
e) 32
APRENDIZAJES ESPERADOS
• Comprender el empleo de la proporcionalidad en triángulos semejantes.
• Reconocer las figuras más frecuentes relacionadas a la semejanza.
• Resolver problemas tipo examen de admisión ya que es un tema frecuente.
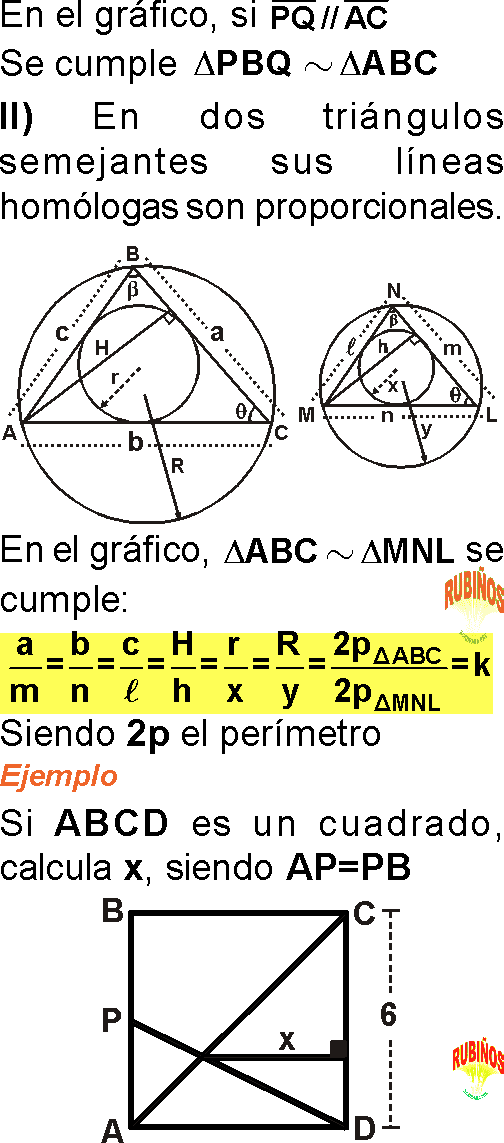
SEMEJANZA DE TRIÁNGULOS
Dos triángulos semejantes son aquellos que tienen la misma forma pero diferente tamaño.
Si tienen 2 pares de ángulos de igual medida, dichos triángulos serán semejantes y podemos construir la igualdad de fracciones
CASOS DE SEMEJANZA DE TRIÁNGULOS
CASO 1: ÁNGULO - ÁNGULO (A-A)
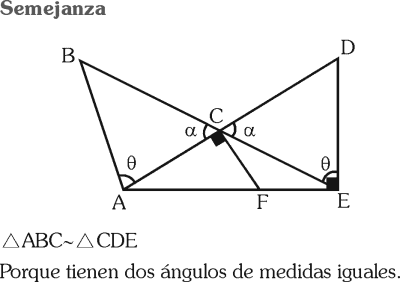
Dos triángulos son semejantes si tienen al menos dos ángulos respectivamente congruentes.
CASO 2: LADO-ÁNGULO-LADO (L-A-L)
Dos triángulos son semejantes si tienen un ángulo congruente y los lados que lo determinan son respectivamente proporcionales.
CASO 3: LADO-LADO-LADO (L-L-L)
Dos triángulos son semejantes si sus lados son respectivamente proporcionales.
Con la medida a escala relacionamos la distancia o tamaño real que hay en una maqueta, plano o mapa.
En muchas actividades que el hombre realiza, día a día, adquiere nuevas destrezas y genera conocimientos para el bien de su sociedad.
Por ejemplo, en la fotografía, la perspectiva de un objeto puede engañar la vista del hombre, tal como ocurre con una cámara que nos muestra una toma distinta desde diferentes ángulos y en ese proceso está presente la proporcionalidad, que también es muy utilizada en la arquitectura con las maquetas, en la informática con sus gráficos, en la ingeniería con sus edificaciones, etc.
Una herramienta diaria que también nos muestra diversos cambios en el tamaño de las copias e impresiones es la fotocopiadora.
Con este conjunto de ideas podemos comparar longitudes o tamaños inmensamente grandes o inaccesibles de medir con longitudes, distancias o tamaños que sean pequeños o fáciles de medir.
Es decir, la muestra de un objeto ayuda a conocer su volumen total sin necesidad de mucho esfuerzo por parte del observador o analista.
Por ejemplo, se puede medir la altura de un edificio con tan solo tener su fotografía.
