RELACIONES MÉTRICAS EN TRIÁNGULOS RECTÁNGULOS EJERCICIOS RESUELTOS PDF
APRENDIZAJES ESPERADOS
• Conocer las relaciones métricas en el triángulo rectángulo.
• Entender el concepto de proyección ortogonal.
• Aplicar los teoremas adecuadamente en la resolución de problemas.
En todo triángulo rectángulo sus lados se relacionan mediante el famoso teorema de Pitágoras. En este capítulo veremos otras relaciones interesantes .
PROYECCIONES
Las proyecciones son las imágenes que se forman sobre una superficie cuando los objetos son iluminados por una luz.
Un caso particular, son las proyecciones ortogonales o perpendiculares
PROYECCIÓN ORTOGONAL DE UN PUNTO:
La proyección ortogonal de un punto sobre una recta, es el pie de la perpendicular trazada por dicho punto a la recta.
PROYECCIÓN ORTOGONAL DE UN SEGMENTO :
La proyección ortogonal de un segmento sobre una recta o eje de proyección es la parte del eje de proyección comprendida entre las proyecciones de los extremos de dicho segmento.
RELACIONES MÉTRICAS EN EL TRIÁNGULO RECTÁNGULO
I) TEOREMA DE PITÁGORAS :
En todo triángulo rectángulo el cuadrado de la longitud de su hipotenusa es igual a la suma de los cuadrados de las longitudes de sus catetos.
II) TEOREMA DEL CATETO :
En todo triángulo rectángulo, el cuadrado de la longitud de un cateto es igual al producto de las longitudes de la hipotenusa y la proyección de dicho cateto sobre la hipotenusa.
III) TEOREMA DE LA ALTURA :
En todo triángulo rectángulo el cuadrado de la longitud de su altura relativa a la hipotenusa es igual al producto de las longitudes de las proyecciones de los catetos sobre la hipotenusa.
IV) En todo triángulo rectángulo, el producto de las longitudes de sus catetos es igual al producto de las longitudes de la hipotenusa y la altura relativa a dicha hipotenusa.
V) En todo triángulo rectángulo la inversa del cuadrado de la longitud de la altura relativa a la hipotenusa es igual a la suma de las inversas de los cuadrados de las longitudes de sus catetos.
PRACTICA
PREGUNTA 1 :
En el trapecio rectángulo la base menor y la altura mide 8 y 14 respectivamente. Hallar la medida de la base mayor, si la diagonal menor es perpendicular al mayor lado no paralelo.
A) 32,5
B) 22,5
C) 32
D) 31,5
E) 31
Rpta. : "A"
PREGUNTA 2 :
Los lados de un triángulo miden 9 ; 16 y 18. ¿Qué longitud "x" se debe restar a cada lado para que el triángulo resultante sea triángulo rectángulo?
A) 3
B) 2
C) 1
D) 4
E) 5
Rpta. : "C"
PREGUNTA 3 :
Se tiene un trapecio de diagonales perpendiculares las cuales miden 12 y 9. Calcular la mediana de dicho trapecio.
A) 8,5
B) 7,5
C) 3,2
D) 9,5
E) 11
Rpta. : "D"
PREGUNTA 4 :
Calcular la suma de los catetos de un triángulo rectángulo con la altura relativa a la hipotenusa sabiendo que las proyecciones de los catetos sobre dicha hipotenusa miden 9 y 16.
A) 46
B) 52
C) 38
D) 39
E) 47
Rpta. : "E"
PREGUNTA 5 :
Se tiene el rectángulo ABCD, cuyos lados AB y AD miden 4 y 6 respectivamente. Sobre el lado BC se ubica el punto P, de tal manera que el cuadrilátero APCD es circunscriptible. Calcular la longitud del inradio del triángulo ABP .
A) 3m
B) 2,5
C) 2
D) 1,5
E) 1
Rpta. : "E"
PREGUNTA 6 :
El punto de tangencia de la circunferencia inscrita en un trapecio rectángulo , divide al mayor de los lados no paralelos en dos segmentos que miden 1m y 9m respectivamente. Luego la base mayor mide :
A) 12m
B) 10m
C) 13m
D) 14m
E) 16m
Rpta. : "A"
PREGUNTA 7 :
Indicar la proyección de un cateto que mide 6 sobre la hipotenusa que mide 9.
a) 2
b) 3
c) 4
d) 5
e) 6
PREGUNTA 8 :
Calcular la altura relativa a la hipotenusa en un triángulo cuyos catetos miden 6 y 8.
a) 3,6
b) 4,8
c) 5,2
d) 7,6
e) 3,8
PREGUNTA 9 :
La hipotenusa y un cateto de un triángulo rectángulo miden 29 y 21 cm. Calcular la longitud del otro cateto.
a) 18 cm
b) 16
c) 20
d) 22
e) 23
PREGUNTA 10 :
Hallar la longitud del mayor cateto de un triángulo rectángulo, cuyos lados están en progresión aritmética de razón 3.
a) 9
b) 12
c) 15
d) 18
e) 21
PROBLEMAS RESUELTOS
PREGUNTA 1 :
En un triángulo rectángulo, la longitud de uno de sus catetos es BC=√2. Si el otro cateto tiene por longitud la tercera parte de la hipotenusa, calcule la longitud de la hipotenusa.
A) 0,5
B) 1
C) 1,5
D) 2
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 2 :
En la siguiente figura, CD es tangente, CD=2√21cm, AB=diámetro y BC=6cm; hallar la medida del radio de la circunferencia.
A) 1 cm
B) 2 cm
C) 3 cm
D) 4 cm
E) 5 cm
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 3 :
En el gráfico mostrado, PA=9, RG=7 y PG=8.
A) 5
B) 5,5
C) 6
D) 6,5
E) 9
RESOLUCIÓN :
Relaciones métricas en triángulo rectángulo
Por teorema Pitágoras
R²=9²+(8 – x)²
⇒ R²=72+x²
⇒ 9²+(8 – x)²= 7²+x² ⇒ x=6
Rpta. : "C"
PREGUNTA 4 :
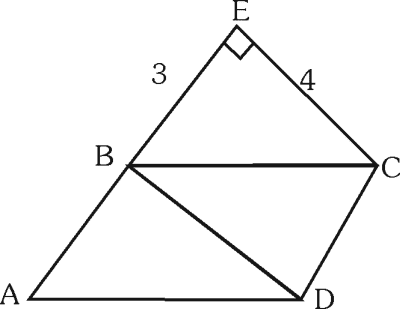
En el triángulo, ABCD es un paralelogramo, BE=3 y EC=4. Calcula EC/AD
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 5 :
En un triángulo rectángulo ABC, recto en B, la altura relativa a la hipotenusa mide √24 y determina dos segmentos proporcionales a 2 y 3. Calcula el cateto BC.
A) 4√2
B) 2√15
C) 7√5
D) 9√3
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 6 :
En un triángulo rectángulo ABC se prolonga la hipotenusa hasta un punto D.
Si BC=CD=7 y AD=32, calcule la altura relativa a la hipotenusa.
A) 6,25
B) 6,72
C) 5,12
D) 5,25
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 7 :
Se tiene una semicircunferencia de diámetro AB y de radio 4. Calcula x+y.
A) 3√2 ( √3 + √5 )
B) 2√3 ( √2 + √5 )
C) 2√2 ( √3 + √5 )
D) 2(√3 + √5 )
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 8 :
En una semicircunferencia de diámetro AB=12 cm se inscribe el triángulo ACB, por el centro de la semicircunferencia se traza una paralela de AC interceptando a BC en Q y en P a la tangente trazada a la circunferencia en B. Si BC=8, calcula PB.
A) 2√2
B) 3√2
C) 5√2
D) 10
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 9 :
Del gráfico; el diámetro, AC mide 32μ, BO=4. Si FB⊥AC, calcule el perímetro de la región triangular AFC.
A) 4√6 + 5√10 + 32
B) 8√6 + 7√10 + 32
C) 8√6 + 8√10 + 32
D) 5√3 + 7√8 + 36
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 10 :
En un triángulo rectángulo ABC recto en B. Si M es punto medio de AB y N∈BC, tal que MN es paralela a AC; AN=22 y MC=19. Calcula AC.
A) 21
B) 24
C) 25
D) 26
RESOLUCIÓN :
Rpta. : "D"
► Las escuadras son utilizadas tanto para trazar perpendiculares como para el trazado de paralelas.
► Para la correcta colocación de una escalera telescópica se recomienda que el triángulo rectángulo formado con el poste tenga sus catetos en una relación de uno a cuatro.