REGLA DE TRES COMPUESTA PROBLEMA RESUELTOS PDF
¿Qué es la regla de tres compuesta?
Es una regla de 3 donde intervienen más de dos magnitudes proporcionales.
MÉTODO DE SOLUCIÓN:
Existen varios métodos de solución, en esta caso emplearemos el método de nombrar :
«si la magnitud es directamente proporcional (D.P.) , o inversamente proporcional (I.P.), con la magnitud donde se encuentra la incógnita».
PASOS A SEGUIR :
I) Se reconocen las magnitudes que intervienen en el problema.
II) En la primera fila se colocan los datos y en la segunda fila los demás datos incluido la incógnita.
III) Se compara la magnitud donde se encuentra la incógnita con cada una de las demás , indicando en su parte inferior , si es directamente proporcional por D.P. , o y si es inversamente proporcional por I.P.
IV) Se despeja la incógnita multiplicando la cantidad que se encuentra sobre ella por las diferentes fracciones que se forman en cada magnitud, si son I.P. se copia igual y si son D.P. se copia diferente (se invierte).
APRENDIZAJES ESPERADOS :
☛ Realizar comparaciones con magnitudes proporcionales.
☛ Conocer los diferentes métodos de solución de una regla de 3 compuesta.
☛ Aplicar la regla de 3 compuesta en la resolución de ejercicios.
OBSERVACIÓN:
En la regla de tres compuesta también podemos aplicar lo aprendido en el capítulo de magnitudes proporcionales, recordando que:
(Obreros) I. P. (Rendimiento)
(Obreros) I. P. (Días)
(Obreros) I. P. (h/d)
(Obreros) D. P. (Obra)
(Obreros) D. P. (Dificultad)
APLICACIÓN 1 :
Si tres patas ponen tres huevos en tres días, doce patas.
¿En cuántos días podrán poner doce huevos?
Rpta. : "3 "
APLICACIÓN 2 :
En una competencia de glotones 40 de ellos puede comer 300 panes en 2 días. Si fueran 50 en 3 días.
¿Cuántos panes podrán comer?
Rpta. : "3625"
APLICACIÓN 3 :
Si 60 obreros trabajando 8 horas diarias construyen 320 metros de una obra en 20 días.
¿ En cuántos días 50 obreros trabajando 6 horas diarias construyen 300 metros de la misma obra?
Rpta. : "30"
EJEMPLO 1 :
Doce obreros trabajando 15 días de 8 horas diarias pueden construir 160 m de un muro. ¿Cuántos días se demorarán 10 obreros trabajando 10 horas diarias para construir 200m del mismo muro?
RESOLUCIÓN :
Lo primero que hacemos es reconocer las magnitudes que intervienen y colocamos los dos juegos de datos, la incógnita se debe encontrar en el segundo juego de datos, para luego hacer las comparaciones.
Luego, el valor de la incógnita se hallará multiplicando la cantidad que se encuentra encima de la incógnita por las diferentes fracciones que se forman en cada magnitud, si son I.P. se copia igual y si son D.P. se copia diferente.
Rpta. : "18 días"
EJEMPLO 2 :
10 obreros pueden cavar una zanja en 8 días ha razón de 5 h/d. calcular en cuantos días otros 24 obreros de doble rendimiento a razón de 10 h/d podrán cavar otra zanja de doble longitud que la anterior, pero 2 veces más difícil.
Rpta. : "5 días"
OTRO PROCEDIMIENTO (MÉTODO DE LAS RAYAS)
Para este método tendremos presente el siguiente orden; además por donde pasa la línea se multiplicará y lo mismo sucede con la otra línea; se igualan ambas líneas y encontramos la incógnita.
EJEMPLO 3 :
Se contratan a 5 costureras que hacen 12 vestidos en 15 días , se pretende tener 60 vestidos en 25 días, ¿Cuántas costureras al igual de rápidas , se deberán contratar además de las ya contratadas?
A) 4
B) 6
C) 5
D) 7
E) 10
Rpta. : "E"
OTRO MÉTODO: (PARTE TODO)
Este mecanismo se basa exclusivamente en la suma de las partes con sus respectivos valores de sus magnitudes, es igual a la parte total con sus valores respectivos , de acuerdo al siguiente gráfico ilustrativo podemos observar. Este método es aplicativo para cierto número de problemas, cuando la sumatoria de los trabajos parciales es igual al trabajo total.
EJEMPLO 4 :
Una cuadrilla de 20 obreros, realizan una obra en 30 días , después del décimo día se retiran 5 obreros, al cabo de 20 días el capataz se da cuenta que para terminar la obra se necesita mayor personal . ¿Cuántos obreros tendrán que contratar para entregar la obra en el plazo fijado?
A) 5
B) 10
C) 7
D) 9
E) 20
Rpta. : "B"
PRACTICA
PREGUNTA 1 :
20 monos comen 20 plátanos en 20 minutos. ¿Cuántos monos comerán 70 plátanos en 70 minutos?
A) 70
B) 20
C) 35
D) 40
E) 60
PREGUNTA 2 :
Doce hombres trabajando 8 horas diarias construyen 24 m de una pared en 10 días. ¿Cuántos hombres serán necesarios para construir 20 m de pared continuada en 5 días trabajando 10 horas diarias?
A) 16
B) 15
C)14
D) 13
E) 20
PREGUNTA 3 :
Ocho hombres cavan una zanja de 24 m de largo por 2 de ancho y 2m de profundidad, en 12 días. ¿Cuántos trabajadores con la misma habilidad serán necesarios para cavar otra zanja de 18 m de largo por 3 m de ancho y 4 m de profundidad en 8 días?
A) 18
B) 12
C) 27
D) 30
E) 24
PREGUNTA 4 :
Tres obreros trabajando 4 horas diarias durante 6 días han hecho 12 metros de una zanja. ¿Cuántos obreros se necesitarán para hacer 16 metros de zanja en 2 días trabajando 6 horas diarias?
A) 9
B) 6
C) 5
D) 3
E) 8
PREGUNTA 5 :
80 obreros trabajando 8h/d construyen 480m² de una obra en 15 días. ¿Cuántos días se requieren para que 120 obreros trabajando 10h/d hagan 960m² de la misma obra?
A) 22
B) 30
C) 18
D) 16
E) 20
PREGUNTA 6 :
En un taller 45 mecánicos ensamblan 10 autos en 20 días, ¿Cuántos mecánicos más triplemente eficientes se deberán contratar para ensamblar 60 autos en 30 días más?
A) 14
B) 21
C) 16
D) 24
E) 30
PREGUNTA 7 :
Un total de 72 carpinteros ha trabajado un total de 4800 m² de madera en 90 días. ¿Cuántos días necesitarán 60 carpinteros del mismo rendimiento para trabajar 12000 m² de madera?
A) 270
B) 280
C) 290
D) 260
E) 250
PREGUNTA 8 :
Si 60 hombres pueden cavar una zanja de 800 m³ en 60 días. ¿Cuántos días necesitaran 100 hombres, 50% mas eficientes, para cavar una zanja de 1200 m³ cuya dureza del terreno es 2 veces mas que la anterior?
A) 120
B) 90
C) 80
D) 70
E) 60
PREGUNTA 9 :
Con 8 obreros se puede hacer una obra en 20 días; con 10 obreros 4 veces más rápidos que los anteriores. ¿En cuántos días harán una obra 9 veces más difícil que la anterior?
A) 25
B) 31
C) 33
D) 32
E) 34
PREGUNTA 10 :
16 obreros pueden hacer una obra en 38 días. ¿En cuántos días harán dicha obra si 5 de los obreros aumentan su rendimiento en 60%?
A) 30
B) 31
C) 32
D) 41
E) 48
PREGUNTA 11 :
Una obra debía terminarse en 30 días empleando 20 obreros, trabajando 8 horas diarias. Después de 12 días de trabajo, se pidió que la obra quedase terminada 6 días antes de aquel plazo y así se hizo.
¿Cuántos obreros se aumentaron teniendo presente que se aumento también en 2 horas el trabajo diario?
A) 4
B) 24
C) 44
D) 0
E) 20
PREGUNTA 12 :
Tres obreros abren una zanja cúbica de 216 m³ en 5 días trabajando 10 h/d ¿Cuál será la profundidad de otra zanja cúbica que ha sido abierta por 15 obreros en 10 días trabajando 8 h/d
A) 3m
B) 4m
C) 12m
D) 6m
E) 8m
PREGUNTA 13 :
35 obreros pueden hacer una obra en 27 días, al cabo de 6 días de trabajo se les une cierto número de obreros de otro grupo, de modo que en 15 días más terminaron la obra ¿Cuántos obreros eran del segundo grupo?
A) 10
B) 12
C) 16
D) 14
E) 18
PREGUNTA 14 :
Si 18 obreros realizan la construcción de una casa en 50 días. ¿En cuántos días la harán, si 10 obreros aumentan su rendimiento en 20%?
A) 35
B) 40
C) 36
D) 45
E) 42
PREGUNTA 15 :
Un grupo de 21 obreros ha hecho en 12 días de 8 h/d, L1m. de una carretera, otro grupo de 40 obreros, 20% más eficientes que los anteriores, han hecho L2 m. de la misma carretera en 7 días trabajando 10 h/d. Halle la relación L1/L2.
A) 1/5
B) 3/5
C) 2/5
D) 4/5
E) 1/3
PREGUNTA 16 :
20 hombres trabajaron durante 30 días a 6 h/d para levantar un edificio de 25m. de altura, 12m. de largo y 10m. de ancho. Al terminar este edificio la cuadrilla con 4 hombres menos paso a construir otro edificio de 20m. de alto 14m. de largo y 10m. de ancho, trabajando 7 h/d y con el doble de dificultad. ¿Cuántos días necesitaran para construirlo?
A) 15
B) 30
C) 45
D) 60
E) 75
PREGUNTA 17 :
30 hombres se comprometen terminar una obra en 15 días; al cabo de 9 días solo han hecho los 3/11 de la obra, razón por la cual, el capataz refuerza la cuadrilla con 42 hombres. ¿Con cuántos días de retraso se terminará la obra?
A) 9
B) 4
C) 5
D) 3
E) 6
PREGUNTA 18 :
Se construye una obra con 4 máquinas que trabajan 10 h/d debiendo terminarla en 30 días. Al final del 6to día una de ellas se malogra durante «x» días. Halle el valor de «x» si desde el 7mo día las otras tres máquinas trabajan 12 h/d y cuando se repara la malograda, esta solo puede trabajar 8 h/d, sabiendo que se termina en el plazo estipulado
A) 10
B) 13
C) 14
D) 12
E) 16
PREGUNTA 19 :
Si 20 peones se demoran 15 días de 7 h/d de trabajo en sembrar 50 m² de terreno. ¿Cuántos días de 8 h/d de trabajo se demoraran en sembrar 80m², 15 peones doblemente eficientes?
A) 10
B) 12
C) 14
D) 16
E) 18
PREGUNTA 20 :
15 albañiles han hecho en 12 días 3/4 de un puente; si entonces se retiran 7 albañiles ¿En cuánto tiempo terminaran los restantes?
A) 10
B) 7,5
C) 8
D) 9,5
E) 11
CLAVES – RESPUESTAS : 1)B 2)A 3)C 4)E 5)D 6)B 7)A 8)B 9)D 10)C 11)A 12)C 13)D 14)D 15)B 16)D 17)B 18)D 19)C 20)B
GUIA COMPLEMENTARIA
PROBLEMA 1 :
Un hombre caminando 8 h/d ha empleado 4 días para recorrer 160 km. ¿Cuántas horas diarias debe caminar otro hombre para recorrer 300 km en 10 días?
A) 9
B) 6
C) 5
D) 8
E) 3
Rpta. : "B"
PROBLEMA 2 :
Una familia de 5 personas tomó una pensión durante 6 días y pagó S/. 60. ¿Cuánto pagó otra familia de 4 personas que estuvo alojada en la misma pensión durante dos semanas?
A) 112
B) 120
C) 114
D) 115
E) 150
Rpta. : "A"
PROBLEMA 3 :
Cinco Obreros trabajando 8 horas diarias hacen una obra en 15 días; 10 obreros trabajando 6 horas diarias, ¿En cuántos días harán otra obra de igual característica?
A) 9
B) 6
C) 5
D) 8
E) 10
Rpta. : "E"
PROBLEMA 4 :
Doce hombres tardan 10 días en cavar una zanja de 2 m de profundidad. ¿Cuántos hombres serán necesarios para cavar otra zanja de 3 m de profundidad en 20 días?
A)10
B)11
C)12
D)9
E)8
Rpta. : "D"
PROBLEMA 5 :
Un cilindro de aguardiente que tiene 30cm de radio y 1m de altura cuesta 120 nuevos soles. ¿Cuánto costara otro cilindro de 25cm de radio y 1,2m de altura?
A) 72
B) 84
C) 97
D) 100
E) 170
Rpta. : "D"
PROBLEMA 6 :
Caminando 6 horas diarias, un hombre ha empleado 4 días para ir de un pueblo a otro distantes entre sí 96 km. Si continuando su viaje debe ir a otro pueblo distante 192 km de este último, ¿ cuántos días empleará caminando 8 horas diarias?
A) 6
B) 3
C) 5
D) 8
E) 7
Rpta. : "A"
PROBLEMA 7 :
En 12 días, 8 obreros han hecho los 2/3 de una obra, en ese momento se retiran 6 obreros. ¿Cuántos días demorarán los obreros restantes en terminar la obra?
A) 20
B) 21
C) 22
D) 24
E) 25
Rpta. : "D"
PROBLEMA 8 :
Doce hombres trabajando 8 horas diarias pueden hacer un muro en 15 días. ¿En cuántos días harán otro muro igual 15 hombres trabajando 6 horas diarias?
A) 14
B) 15
C)16
D)17
E) 18
Rpta. : "C"
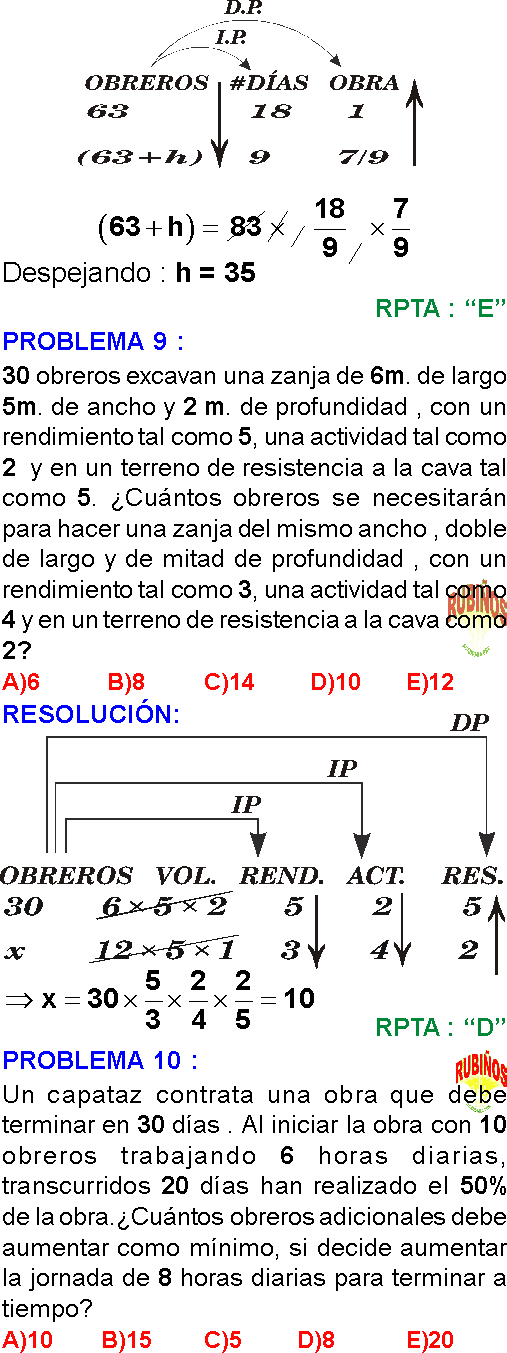
PROBLEMA 9 :
Un ingeniero civil se compromete a hacer una obra que comenzaría el 1ro. de abril y terminaría el 5 de mayo trabajando domingos y feriados inclusive. El 1ro. de abril pone a trabajar a 20 hombres, los cuales trabajan a razón de 6 horas diarias. Al terminar la jornada del día 14 de abril, el propietario le dice que necesita la obra terminada el día 24 de abril. Entonces a partir del 15 se coloca más hombres que trabajen 9h/d en vez de 6 y logra complacer al propietario. ¿Cuántos hombres aumentó el ingeniero a partir del 15 de abril?.
A) 16
B) 10
C) 2
D) 6
E) 8
Rpta. : "E"
PROBLEMA 10 :
En un prado cuadrado de 100 metros de lado hay cuatro cabras. Cada una atada a una esquina del prado con una cuerda de 50 metros, lo que les permite comer una cierta parte de la hierba del prado, quedando en el centro un trozo que ninguna de ellas alcanzó. El propietario, tras vender tres de las cabras, alargó la cuerda de la que quedaba en una de las esquina, de tal forma que el área sobre la que podía pasar era equivalente al área sobre la que pasaban anteriormente las cuatro. ¿ qué longitud le dio a la cuerda?
A) 200 m.
B) 50
C) 8
D) 400
E)100
Rpta. : "E"
PROBLEMA 11 :
Una cuadrilla de hombres debe cegar dos prados , uno tenía el doble de superficie que el otro. Durante medio día trabajó todo el personal en el prado más grande ; después del almuerzo, la mitad de la cuadrilla siguió trabajando en el prado más grande y la otra mitad lo hizo en el más pequeño, durante esa tarde fueron terminados los dos prados, a excepción de un reducido sector del prado más pequeño cuya siega ocupó el día siguiente completo a un sólo hombre. ¿Cuántos hombres formaban la cuadrilla de segadores?
A) 8
B) 5
C) 10
D) 12
E) 4
Rpta. : "A"
PROBLEMA 12 :
Una obra se ha dividido en 3 partes y la pueden realizar con cierta cantidad de obreros, la primera parte en 10 días trabajando 8h/d , la segunda parte en 8 días trabajando 6h/d y la tercera parte en 12 días trabajando 10h/d. Calcular cuántas horas deben trabajar la mitad de dichos obreros en realizar toda la obra en 31 días.
A) 12 horas
B) 14 horas
C) 16 horas
D) 13 horas
E) 18 horas
Rpta. : "C"
PROBLEMA 13 :
En una comarca ha llovido sin interrupción y con la misma intensidad día y noche, durante 30 días. Al empezar el temporal tres pozos para acumular el agua de lluvia tenían la misma altura de agua en todos ellos. Se sabe que el primer pozo, de 60m² de superficie ha servido para abastecer a 20 personas durante los 30 días de lluvia , quedando luego vacío, el segundo, de 15m² ha abastecido a 6 personas durante los 20 primeros días de lluvia hasta que queda vacío ¿a cuántas personas abastecerá el tercero, de 75m² que se ha vaciado en 25 días; si se sabe que todas las personas consideradas consumen el mismo número de litros de agua por día. No se debe tener en cuenta el agua que recogen los pozos pasado el instante en que su nivel se hace cero.
A) 26
B) 25
C) 27
D) 30
E) 45
Rpta. : "C"
PROBLEMA 14 :
15 obreros se comprometen a realizar una obra en «d» días, trabajando 8 h/d , después de 10 días, 10 obreros se enferman y disminuyen su rendimiento al 75% y 10 días más tarde ellos se retiran, motivo por el cual desde este momento los obreros restantes aumentan su jornada en 2 h/d; si dicha obra se entregó con un retraso de 46 días. Calcular el valor de «d.
A) 40 días
B) 30 días
C) 45 días
D) 50 días
E) 35 días
Rpta. : "D"
PROBLEMA 15 :
En una sastrería los sastres A; B y C confeccionar 5; 6 y 7 ternos respectivamente en un mismo tiempo. Además, A y B juntos confeccionan 8 ternos en 28 días. ¿En cuantos días confecciona “C” 4 ternos?
A) 21
B) 18
C) 19
D) 22
E) 24
Rpta. : "D"
PROBLEMA 16 :
Un hombre con dos mujeres pueden hacer una obra en 10 días. Determinar el tiempo necesario para que 2 hombres con 1 mujer puedan hacer el trabajo que tiene 4 veces la dificultad del anterior sabiendo que el trabajo de un hombre y el de una mujer está en la misma relación que los números 3 y 2.
A) 25
B) 28
C) 35
D) 30
E) 40
Rpta. : "C"
PROBLEMA 17 :
Un grupo de 15 obreros abrieron una zanja de 2 m de ancho, 1,2 m de profundidad y 100 m de largo, en 28 días. Luego otro grupo de 12 obreros del triple de rapidez que los anteriores, en 21 días abrieron otra zanja de 1,8 m de ancho y 1,5 m de profundidad. La longitud de la segunda zanja es:
A) 100 m
B) 110 m
C) 120 m
D) 150 m
E) 160 m
Rpta. : "E"
PROBLEMA 18 :
Dieciocho obreros hacen en 8 días los 1/3 de una obra; si en los siguientes 3 días por día ingresan “x” obreros más, concluyendo la obra, hallar “x”.
A) 12
B) 20
C) 30
D) 18
E) 15
Rpta. : "D"
PROBLEMA 19 :
Si se sabe que un ama de casa puede lavar con 50 gramos de detergente 12 pantalones al día por un periodo de 6 días o 15 camisas diarias durante 4 días. ¿Cuántos gramos de detergente necesitará para lavar 3 pantalones y 4 camisas por día durante 15 días?
A) 81,25 g
B) 81,5 g
C) 81,20 g
D) 85,25 g
E) 82,15 g
Rpta. : "A"
PROBLEMA 20 :
Si una cuadrilla de 20 hombres pueden hacer un trabajo en 15 días, otra formado por 10 hombres hacen el mismo trabajo en 30 días. ¿Cuántos hombres mas se necesitarán para realizar el trabajo en los 3/5 parte del tiempo empleado por los 30 hombres?
A) 15
B) 18
C) 20
D) 25
E) 30
Rpta. : "C"
PROBLEMA 21 :
¿Qué cantidad de obreros pueden hacen una obra en 12 días trabajando 6 horas diarias, después de iniciado se quiere terminar en 8 días, reduciendo 1/6 de la obra y aumentando a 8 horas diarias el trabajo diario? ¿cuántos días trabajaron 8 horas diarias?
A) 16 días
B) 10 días
C) 5 días
D) 7 días
E) 8 días
Rpta. : "E"
PROBLEMA 22 :
Se contratan “2n” obreros para hacer una obra y a partir del segundo día se despedirá 1 obrero cada día hasta terminar la obra, trabajando el último día un solo obrero. Calcular “n”, sabiendo que, si hubiesen trabajado “n” obreros sin despido alguno, terminarían la obra en 37 días.
A) 15
B) 18
C) 20
D) 21
E) 25
Rpta. : "B"
PROBLEMA 23 :
Si por en mayolicar las paredes y piso de una cocina de 3 m de largo, 2 m de ancho y 2 m de alto se pagó 3 200 nuevos soles. ¿Cuánto se pagará por enmayolicar solo las paredes de otra cocina del doble de largo, una vez mas de ancho y siendo 1/8 menos de alto, si el costo de enmayolicar la pared es la mitad al del piso?
A) 7 900
B) 11 900
C) 4 500
D) 8 300
E) 9 500
Rpta. : "D"
PROBLEMA 24 :
Para pintar las paredes de una sala rectangular de 10 m de largo, 6 m de ancho y 2 m de altura pago 5 600 nuevos soles. ¿Cuánto se pagará por pintar las paredes de un dormitorio de 3m×2m×2m?
A) 1 750
B)1 900
C) 2 150
D)1 000
E) 1 650
Rpta. : "A"
PROBLEMA 25 :
25 obreros hacen 5/8 de una obra en 10 días. A partir de ese momento se contrata “n” obreros más cada día, terminando 2 días antes de la fecha en que terminarían los 25 obreros si hubiera continuado la obra solos. Halle “n”.
A) 3
B) 2
C) 4
D) 5
E) 6
Rpta. : "D"