REDUCCIÓN AL PRIMER CUADRANTE EJERCICIOS RESUELTOS PDF
¿Qué es la reducción al primer cuadrante?
Es el método por el cual se calcula las razones trigonométricas de ángulos que son mayores que 90°, en términos de un ángulo agudo o menor que 90°.
APRENDIZAJES ESPERADOS
• Calcular las razones trigonométricas de un ángulo cualquiera, expresándolo en función de un ángulo agudo, reconociendo para ello el caso en que nos encontremos .
Utilizando las formas : 𝟗𝟎°±𝜽 ; 𝟏𝟖𝟎°±𝜽 ; 𝟐𝟕𝟎°±𝜽 ; 𝟑𝟔𝟎°−𝜽 ; 𝟑𝟔𝟎°𝒏+𝜽
• Aplicar los signos de las razones trigonométricas de acuerdo a la medida del ángulo.
• Utilizar la reducción al primer cuadrante para casos especiales, como son los ángulos complementarios y suplementarios.
• Adaptar la teoría a la resolución de determinadas situaciones geométricas.
Un ángulo puede hallarse situado en cualquiera de los cuatro cuadrantes de que consta la circunferencia, dependiendo de su posición los valores de sus correspondientes líneas trigonométricas. Pues bien, cuando un ángulo se encuentra situado en el segundo, en el tercero o en el cuarto cuadrante siempre es posible relacionarlo con otro ángulo del primer cuadrante cuyas líneas trigonométricas tengan los mismos valores absolutos, esto es, de los mismos valores salvo posiblemente el signo.
Las relaciones entre las líneas trigonométricas de los ángulos situados en los distintos cuadrantes resultaba esencial cuando no se disponía de calculadoras.
Existían tablas con los valores de las razones para ángulos del primer cuadrante. Los demás ángulos no figuraban en la tabla pues no era necesario: bastaba con reducirlo al primer cuadrante. No obstante, el tema sigue siendo de interés para aplicar las razones trigonométricas inversas, es decir, para determinar un ángulo conocida una de sus razones trigonométricas.
Como sabemos, si buscamos un ángulo a partir de una razón trigonométrica, la calculadora nos proporciona sólo una solución. Nosotros encontraremos el resto de soluciones con los conocimientos adquiridos en esta unidad.
REDUCCIÓN AL PRIMER CUADRANTE
Es el procedimiento mediante el cual se calcula las razones trigonométricas de ángulos que no son agudos, en términos de un ángulo que si lo sea.
ÁNGULO DE REFERENCIA
Al ángulo agudo formado por el lado final de un ángulo positivo en posición normal θ con el lado positivo o negativo del eje “X” se llama ÁNGULO DE REFERENCIA y se denota por θR .
PROPIEDAD FUNDAMENTAL
Si θ es un ángulo positivo normal menor que una vuelta y θR su ángulo de referencia, entonces se cumple que las R.T. de θ y los R.T. de θR va a tener los mismos valores y en algunos casos difieren en el signo
CASOS DE REDUCCIÓN AL PRIMER CUADRANTE
En los ejemplos anteriores se ha notado que efectivamente las razones trigonométricas de su respectivo ángulo de referencia en algunos casos difieren en el signo.
Para hacer cálculos directos vamos a citar los siguiente casos :
✎ Cuando se trata de ángulos positivos menores a una vuelta
✎ Cuando se trata de ángulos positivos mayores a una vuelta
✎ Cuando se trata de ángulos negativos
REDUCCIÓN PARA ÁNGULOS POSITIVOS MENORES A UNA VUELTA
Todo ángulo positivo menor a una vuelta se puede descomponer como un ángulo cuadrantal más o menos un ángulo agudo, dependiendo del cuadrante al que pertenece i) Mantener la misma razón trigonométrica si el ángulo está próximo al eje horizontal iii) El signo que tendrá la operación de reducción será el mismo que posee la razón trigonométrica en el cuadrante al cual pertenece el ángulo.
REDUCCIÓN PARA ÁNGULOS POSITIVOS MAYORES A UNA VUELTA :
Si a un ángulo positivo “θ” mayor que una vuelta lo dividimos entre 360° nos da como cociente “n” y residuo “θ” Es decir para este caso bastará con dividir el ángulo entre 3600 o su equivalente 2𝛑 rad, para finalmente tomar la misma razón trigonométrica al residuo o arco sobrante.
Si el residuo no pertenece al primer cuadrante, deberá utilizarse la reducción explicada en el item anterior.
Si el residuo es menor que 90° (𝛑/2 rad) el problema habrá concluido. Aquí se observa que si a un ángulo de una razón trigonométrica se elimina el número entero de vueltas que contiene, el valor de dicha razón no varía .
REDUCCIÓN PARA ÁNGULOS NEGATIVOS
Para reducir al primer cuadrante las razones trigonométricas de un ángulo negativo, primero pasaremos de ángulos negativos a positivos
✎ sen(–x) = – senx
✎ cos(–x) = +cosx
✎ tg(–x) = – tgx
✎ ctg(–x) = – ctgx
✎ sec(–x) = +secx
✎ csc(–x) = cscx
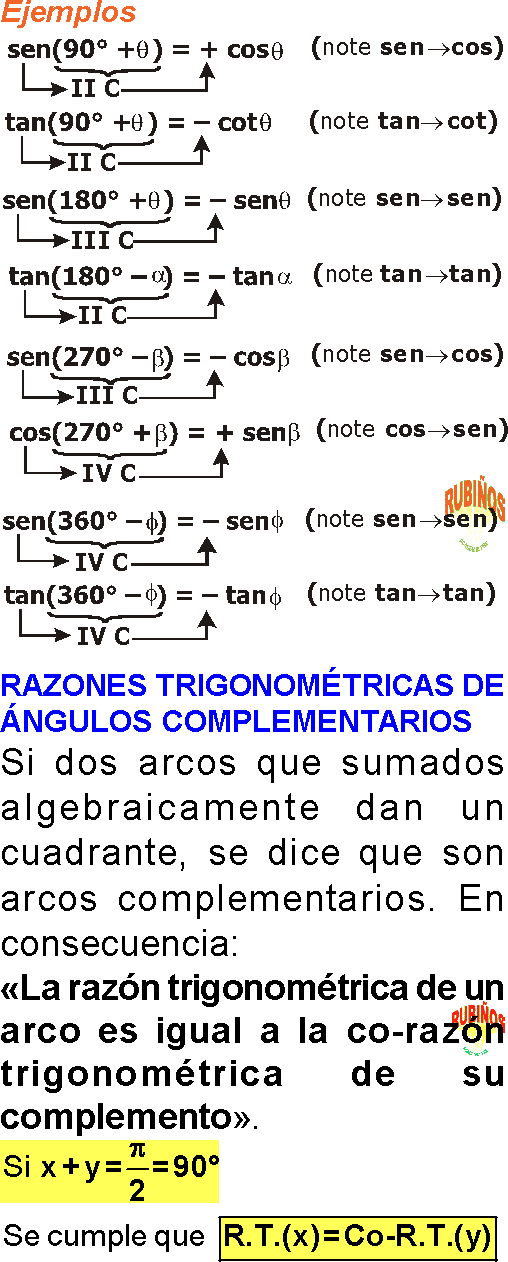
RAZONES TRIGONOMÉTRICAS DE ÁNGULOS COMPLEMENTARIOS :
Si dos arcos que sumados algebraicamente dan un cuadrante, se dice que son arcos complementarios.
RAZONES TRIGONOMÉTRICAS DE ÁNGULOS SUPLEMENTARIOS :
Si dos arcos que sumados algebraicamente dan dos cuadrantes, se dice que son arcos suplementarios.
En consecuencia: «La razón trigonométrica de un arco es igual a ± la razón trigonométrica de su suplemento».
PRIMERA PRACTICA
EJERCICIO 1 :
Calcular: sen120º
EJERCICIO 2 :
Calcular: cos150º
EJERCICIO 3 :
Calcular: tg135º
EJERCICIO 4 :
Calcular: ctg225º
EJERCICIO 5 :
Calcular: sec150º
EJERCICIO 6 :
Calcular: csc240º
EJERCICIO 7 :
Calcular: tg225º
EJERCICIO 8 :
Calcular: sen120ºcos225º
EJERCICIO 9 :
Calcular: sen150ºcos240º
EJERCICIO 10 :
Calcular: cos330º + sen240º
EJERCICIO 11 :
Calcular: cos(–37º) + tg(–45º)
EJERCICIO 12 :
Calcular: sen(–30º)cos(–45º)
EJERCICIO 13 :
Calcular: cos(–60º) + tg(–37º)
EJERCICIO 14 :
Calcular: sen(–30º) + tg(–53º)
EJERCICIO 15 :
Calcular: 2sen240º + tg120º
EJERCICIO 16 :
Simplificar: tg(90º + x)cos(270º – x) .
EJERCICIO 17 :
Calcular: tg(360º – x)tg(270º – x)
EJERCICIO 18 :
Calcular: sen750º
EJERCICIO 19 :
Calcular: cos540º
EJERCICIO 20 :
Calcular: tan900º
EJERCICIO 21 :
Reducir al primer cuadrante: sen3010º
EJERCICIO 22 :
Calcule: tg1837°
EJERCICIO 23 :
Determine: sen2280°
EJERCICIO 24 :
Calcule: cos1277°
EJERCICIO 25 :
Determine el valor de: sen2280°
EJERCICIO 26 :
Simplifique:
sec²2385° + tg²1680°
EJERCICIO 27 :
Calcule: tg(– 45°)ctg(–60°)
EJERCICIO 28 :
Reduce: 3sen(–x)cscx + 2cos(–x)secx
EJERCICIO 29 :
Calcule: tg(–2040°) + tg(–2460°)
SEGUNDA PRACTICA
PREGUNTA 1 :
Calcula Sec135°.Csc150°
A) √3
B) 1
C) –2√2
D) 3
E) –√3
Rpta. : "C"
PREGUNTA 2 :
Calcula Cos210° – Tg120°
A) 2
B) 1
C) –1
D) √3/2
E) –√3
Rpta. : "D"
PREGUNTA 3 :
Calcula Sen225°.Cos210°
A) √2/8
B) 1
C) √5
D) √6/4
E) –3
Rpta. : "C"
PREGUNTA 4 :
Calcula Sen210° +Cos60°
A) 0
B) 1
C) –1
D) 3
E) –3
Rpta. : "A"
PREGUNTA 5 :
Si Cos10° = a ¿A qué es igual?
E = Sen100° . Cos190°
a) a²
b) – a²
c) 1
d) a³
e) –a³
Rpta. : "C"
PREGUNTA 6 :
Si: Sen40° = k ¿A que es igual?
E = Sen140°.Cos130°
a) k
b) k²
c) k−¹
d) k⁴
e) k−⁴
Rpta. : "C"
PREGUNTA 7 :
Reduce al primer cuadrante Tan 870°.
A) √3
B) 1
C) –√3/3
D) 3
E) –√3
Rpta. : "C"
PREGUNTA 8 :
Reduce al primer cuadrante Sen 1215°
A) √2/2
B) 1
C) –√2/4
D) 3
E) –3
Rpta. : "A"
PREGUNTA 9 :
Reduce al primer cuadrante. Tan10000°
a) Tan80°
b) –Tan80°
c) Tan70°
d) –Tan70°
e) –Tan10°
Rpta. : "B"
PREGUNTA 10 :
Reduce al primer cuadrante Sen8230°
a) Sen10°
b) Sen22°
c) –Sen50°
d) Sen50°
Rpta. : "C"
PREGUNTA 11 :
Calcule
R= tan²1500°+ 5cos2483°
A) 4
B) 5
C) 6
D) 7
Rpta. : "D"
PREGUNTA 12 :
Si tan(720°+x) + cot(360°+x) = 3
Calcule senx cosx
A) 1/2
B) − 1/2
C) − 1/3
D) 1/3
Rpta. : "D"
PREGUNTA 13 :
Calcula
(Sen750° − Cos1500°)÷(Sen1430° + Cos1510°)
A) 0
B) 1
C) –1
D) 3
E) –3
Rpta. : "A"
PREGUNTA 14 :
Calcula
(Sen1490° − Cos1120°)÷(Tan765° − Tan1860°)
A) –1
B) 1
C) 0
D) 3
E) –3
Rpta. : "C"
PROBLEMAS RESUELTOS
PREGUNTA 1 :
Si 0 < x < 𝛑/2
calcula:
cos(x+𝛑)+cos(x+𝛑/2)+cos(x – 𝛑)+tg(x+𝛑)cos(x+𝛑)
A) senx – 2cosx
B) 3senx
C) 2senx
D) –2senx – 2cosx
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 3
En la siguiente figura, calcular el valor de la expresión:
A) 0
B) 1
C) –1
D) 2
E) –2
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 4 :
Si: sen(𝛑/2 + α ) – cos(α – 𝛑)= 1/2
Calcular : cosα+senα tgα
A) 1
B) 2
C) 3
D) 4
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 5 :
Sean α, β y θ ángulos internos de un triángulo, al reducir la siguiente expresión :
E = senα + sen(β + θ ) + sen(α + β + θ )
A) senα
B) 2senα
C) 0
D) – senα
E) – 2senα
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 6 :
A) 1
B) – 1
C) 2
D) – 2
RESOLUCIÓN :
Rpta. : "B"
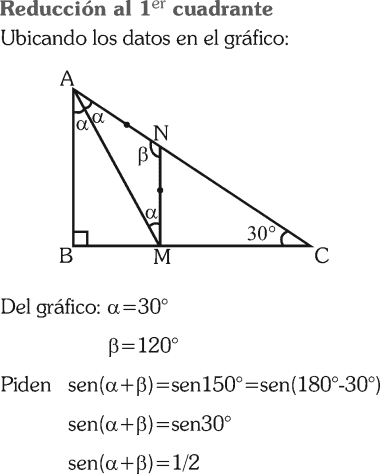
PREGUNTA 8 :
En el gráfico, AM es bisectriz del ángulo BAC; el ∠ACB=30°. Además α=∠NAM y β=∠MNA, siendo AN=NM; calcule sen(α+β)
A) 1/2
B) 3 /2
C) 2 /2
D) 3/5
RESOLUCIÓN :
Rpta. : "A"