PUNTOS NOTABLES EJERCICIOS RESUELTOS PDF – GEOMETRÍA
PROBLEMAS RESUELTOS
PREGUNTA 1 :
En un triángulo acutángulo ABC de circuncentro O, la m∢ABC=65º. Halle la m∢OAC.
A) 20º
B) 30º
C) 40º
D) 35º
E) 25º
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 2 :
En un triángulo acutángulo ABC de circuncentro O, AO=4 y la m∢BAC=60º. Halle BC.
A) 4
B) 4√3
C) 4√2
D) 8
E) 2 2
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 3 :
En una región triangular ABC de baricentro G, BG=4, AG=2√3 y m∢AGB=90º. Halle la m∢GAC.
A) 37º
B) 22,5º
C) 30º
D) 53º
E) 60º
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 4 :
En un triángulo acutángulo ABC de circuncentro O, las cevianas interiores AE y CD se intersecan en O. Si la m∢ABC=40º, m∢ADO=4x y la m∢OEC=6x. Halle el valor de x.
A) 10º
B) 12º
C) 15º
D) 18º
E) 20º
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 5 :
En un triángulo ABC, m∢A=m∢C=30° y AC=6m. Halle la distancia del circuncentro del triángulo ABC al excentro relativo al lado BC.
A) 2√2 m
B) 2√3 m
C) 3√6 m
D) 2√6 m
E) 3 m
RESOLUCIÓN :
Rpta. : "D"
OBJETIVOS DEL APRENDIZAJE
• Conocer las propiedades de concurrencia de las líneas notables.
• Estudiar ciertas propiedades de triángulos con las circunferencias que se las asocia.
• Relacionar correctamente los teoremas con los ejercicios.
• Reconocer el punto de concurrencia de las alturas o sus prolongaciones en los distintos triángulos.
• Analizar al Circuncentro a partir del centro de una circunferencia.
• Resolver problemas tipo examen de Admisión.
PROBLEMA 1 :
Indique el valor de verdad o falsedad de las siguientes proposiciones:
I) En todo triángulo equilátero el baricentro, el incentro, el ortocentro y el circuncentro son el mismo punto.
II) En todo triángulo isósceles el baricentro, el incentro, el ortocentro y el circuncentro se encuentran en la misma recta.
III) En todo triángulo rectángulo el baricentro, ortocentro y circuncentro se encuentran en la misma recta.
A) VVV
B) VVF
C) VFF
D) FFF
E) FFV
RESOLUCIÓN :
Rpta. : "A"
BARICENTRO
Es el punto de concurrencia de las tres medianas de un triángulo.
• Es suficiente con trazar dos medianas para determinar el baricentro
• El baricentro divide a la mediana en la razón de 2 a 1
INCENTRO
Es el punto de concurrencia de las bisectrices interiores de un triángulo
• Es suficiente con trazar dos bisectrices interiores para determinar el incentro
• El incentro también es el centro de la circunferencia inscrita.
EXCENTRO
Es el punto de concurrencia de dos bisectrices exteriores y una bisectriz interior.
• El excentro también es el centro de la circunferencia exinscrita
ORTOCENTRO
Es el punto de concurrencia de las tres alturas de un triángulo.
CIRCUNCENTRO
Es el punto de concurrencia de las mediatrices de los lados de un triángulo.
Solo en el triángulo equilátero, el baricentro, ortocentro, incentro y circuncentro coinciden en su ubicación.
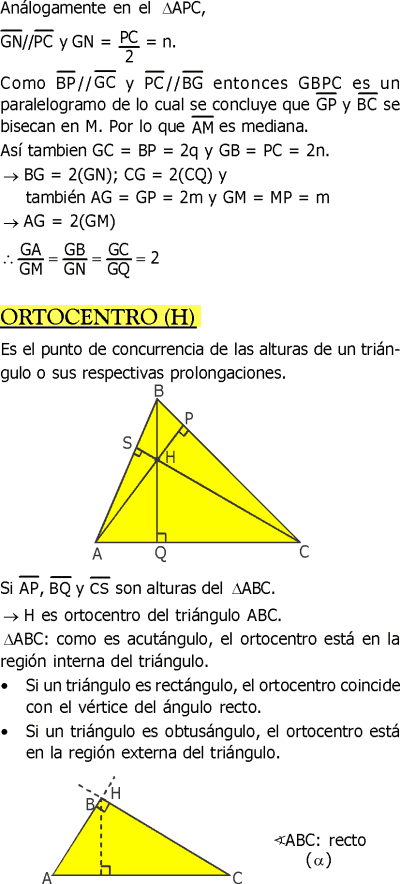
ORTOCENTRO (H)
Es el punto donde concurren las tres alturas de un triángulo o sus prolongaciones.
El ortocentro está ubicado en el interior en un triángulo acutángulo, en el exterior en un triángulo obtusángulo y en el vértice del ángulo recto en un triángulo rectángulo.
BARICENTRO (G)
Es el punto donde concurren las tres medianas de un triángulo.
INCENTRO (I)
Es el punto donde concurren las tres bisectrices interiores.
El incentro es el centro de la circunferencia inscrita y equidista de los lados del triángulo
EXCENTRO (E)
Es el punto donde concurren las bisectrices de dos ángulos exteriores de un triángulo y la bisectriz del tercer ángulo interior.
El excentro es el centro de la circunferencia ex - inscrita y equidista de los lados.
Todo triángulo tiene tres excentros.
CIRCUNCENTRO (O)
Es el punto donde concurren las mediatrices de los lados de un triángulo.
El circuncentro es el centro de la circunferencia circunscrita al triángulo y equidista de los vértices.
El circuncentro está ubicado en el interior de un triángulo acutángulo, en el exterior de un triángulo obtusángulo y en el punto medio de la hipotenusa en un triángulo rectángulo.
TRIÁNGULO MEDIANO O COMPLEMENTARIO
El triángulo mediano o complementario se obtiene al unir los puntos medios de los lados de un triángulo.
El baricentro de un triángulo es a la vez baricentro de su triángulo mediano.
TRIÁNGULO EX - INCENTRAL
El triángulo ex-incentral se determina al unir los excentros de un triángulo. El incentro de un triángulo es a la vez ortocentro de su triángulo ex-incentral.
RECTA DE EULER
En todo triángulo no equilátero se cumple que el ortocentro, baricentro y el circuncentro están contenidos en una misma recta llamada la Recta de Euler.
TRIÁNGULO PEDAL
Es el triángulo cuyos vértices son los pies de las perpendiculares trazadas desde un punto cualquiera, del plano determinado por un triángulo dado, sobre los lados o sus respectivas prolongaciones.
El ortocentro de un triángulo acutángulo es el incentro de su triángulo pedal y cada vértice del triángulo acutángulo es excentro del triángulo pedal.
Al triángulo pedal también se le conoce como triángulo podar.
• Si P coincide con el ortocentro, el triángulo pedal es el triángulo órtico del triángulo.
• Si P coincide con el circuncentro, el triángulo pedal es el triángulo mediano del triángulo.
• Si P coincide con el incentro, el triángulo pedal es el triángulo tangencial.
• Cuando P pertenece a la circunferencia circunscrita, no existe triángulo pedal porque los pies de las perpendiculares son colineales. (recta de Simson).
TRIÁNGULO EXINCENTRAL
Es el triángulo cuyos vértices son los excentros de un determinado triángulo.
TRIÁNGULO TANGENCIAL
Es el triángulo cuyos vértices son los puntos de tangencia de la circunferencia inscrita con los lados del triángulo.
TEOREMA DE CARNOT
En todo triángulo acutángulo, la suma de las distancias del circuncentro a cada lado del triángulo es igual a la suma del circunradio con el inradio de dicho triángulo.
TEOREMA DE NAGEL
En todo triángulo, el segmento que une los pies de dos alturas, es perpendicular, al circunradio relativo al tercer vértice.
PUNTO DE BROCARD
► El ortocentro nos trae a la memoria frases como tengo un tratamiento de ortodoncia, tengo un cuello ortopédico, soy ortopedista, todos ellos se refieren a derecho o recto
► En la naturaleza podemos apreciar la concurrencia de las descargas eléctricas en el cielo.
► Las ramas de diferentes plantas y árboles que presentan concurrencia.
