PROGRAMACIÓN LINEAL EJERCICIOS RESUELTOS PDF
PREGUNTA 1
En un problema de programación lineal, la región factible viene dada por un polígono convexo acotado, cuyos vértices son (0;0), (0;6), (7;6) y (3;0). Sea la función objetivo f, dada por f(x;y)=2x – 2y, entonces el valor máximo de f es:
A) 2
B) 4
C) 6
D) 10
E) 12
Resolución
Se tiene la función objetivo:
f(x;y) =2x–2y
Por dato, la región factible es un polígono convexo acotado cuyos vértices son (0;0); (0;6); (7;6) y (3;0). Entonces evaluamos la función objetivo en dichos vértices.
f(0;0) = 2(0)–2(0) =0
f(0;6) = 2(0)–2(6) =–12
f(7;6) = 2(7)–2(6) =2
f(3;0) = 2(3)–2(0) =6
Obtenemos que el valor máximo de f es
máx f(x;y) = f(3;0) =6
Rpta. : "C"
PREGUNTA 2
Una factoría produce 2 tipos de cocinas: A y B. Producir una cocina del tipo A requiere 2 horas de trabajo en máquina y 2 horas de trabajo a mano. La venta de cada cocina tipo A deja una utilidad de S/40. Por otro lado, producir una cocina tipo B requiere 4 horas de trabajo en máquina y una hora de trabajo a mano. La venta de cada unidad del modelo B deja una utilidad de S/70. Si por día se dispone, en total, de un máximo de 200 horas de trabajo en máquina y 140 horas de trabajo a mano, ¿cuánto es la máxima utilidad diaria?
A) S/2500
B) S/3850
C) S/3800
D) S/4000
E) S/2980
Resolución
Rpta. : "C"
PREGUNTA 3
Determine el valor máximo de la función objetivo f(x; y)=2x+3y sujeta a la restricción:
2y ≤ x+2
y – x ≥ – 1
0 ≤ x ≤ 4
y ≥ 0
A) 13
B) 14
C) 15
D) 16
E) 17
Resolución
Maximizar: f(x; y)=2x+3y
Graficando la región factible:
Evaluando en cada vértice de dicha región:
f(A)=f(0;1)=3
f(B)=f(4;3)=17 ➞ (Máx.)
f(C)=f(1;0)=2
∴fmáx=17
Rpta. : "E"
PREGUNTA 4
Si la función objetivo f(x,y)=ax+3y admite un valor máximo de 39 en la región admisible mostrada.
A) 4
B) 7
C) 64
D)1/2
E) 0
Resolución
Rpta. : "A"
PREGUNTA 6
Un comerciante compra y vende frigoríficos y lavadoras cuyo costo de cada uno es de 500 dólares y 400 dólares respectivamente. Si solo tiene espacio en su almacén para guardar 50 electrodomésticos y 22 000 dólares para invertir. Sabiendo que la ganancia obtenida por un frigorífico es 120 dólares y 100 dólares por una lavadora, ¿cuántos electrodomésticos de cada tipo debe comprar y vender para obtener la máxima ganancia?
A) 30 frigoríficos y 20 lavadoras
B) 10 frigoríficos y 20 lavadoras
C) 20 frigoríficos y 30 lavadoras
D) 44 frigoríficos y 1 lavadora
E) 10 frigoríficos y 30 lavadoras
Resolución
Rpta. : "C"
PREGUNTA 7
En un restaurante se dispone de 26 kg de arroz cocinado y 10 kg de seco de cabrito para vender plato simple o plato a la carta. En cada plato simple, se utiliza 400 g de arroz y 100 g de seco de cabrito y en el plato a la carta, utiliza 300 g de arroz y 250 g de seco de cabrito. Si el plato simple se vende a 14 soles y el plato a la carta a 21 soles, halle el máximo ingreso.
A) S/ 1500
B) S/ 1150
C) S/ 1450
D) S/ 1050
E) S/ 1120
Resolución
Rpta. : "E"
PREGUNTA 8
Un taller produce dos tipos de juegos pirotécnicos, M y N, los que son vendidos a 35 y 40 soles la caja, respectivamente. Por regulaciones municipales, no se debe producir más de 65 cajas del tipo M, ni más de 50 cajas del tipo N por semana. Además, la producción semanal de ambos pirotécnicos no debe superar las 100 cajas. Determine el ingreso máximo semanal que puede obtener por la venta de ambos tipos de pirotécnicos.
A) S/ 3675
B) S/ 3250
C) S/ 3950
D) S/ 3500
E) S/ 3750
Resolución
Rpta. : "E"
PREGUNTA 9
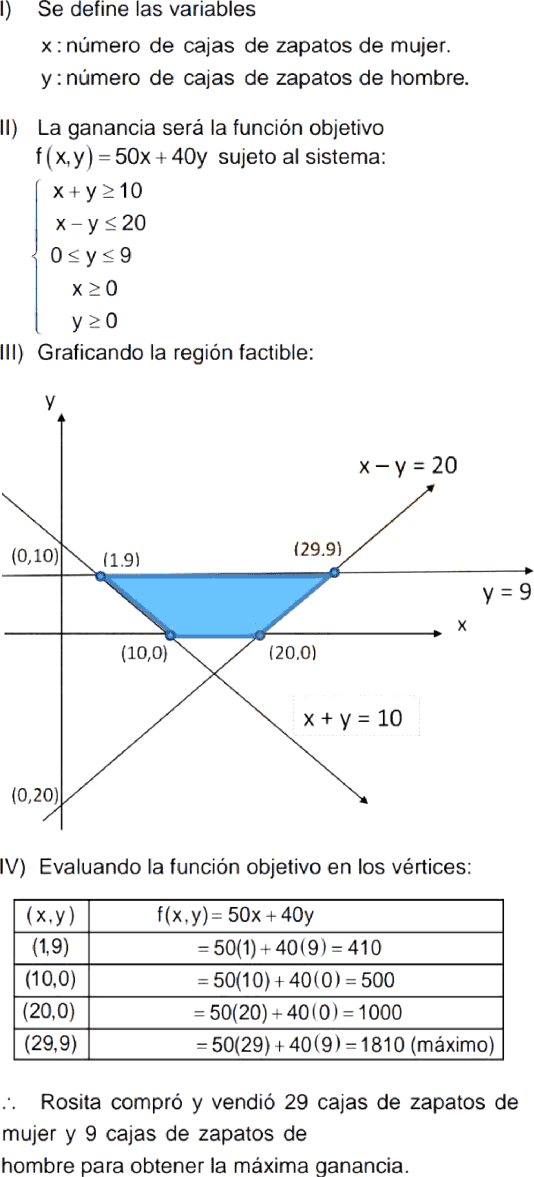
Rosita realiza un viaje a Trujillo para comprar zapatos al por mayor. Ella ha estimado sus ganacias en función al número de cajas de zapatos de mujer y hombre que compra y vende. El número total de cajas de zapatos que compra y vende no es menos que 10, pero la diferencia del número de cajas de zapatos de mujer con el de hombres es a lo más 20, además el número de cajas de zapatos de hombre es a lo mas 9. Si la ganancia por cada caja de zapatos de mujer es 50 soles y cada caja de zapatos de hombre 40 soles, ¿cuántas cajas de zapatos de mujer y hombre compró y vendió Rosita, si obtuvo la máxima ganancia?
A) 20 cajas de zapatos de mujer y 10 cajas de zapatos de hombre
B) 9 cajas de zapatos de mujer y 1 caja de zapatos de hombre
C) 29 cajas de zapatos de hombre y 9 cajas de zapatos de mujer
D) 20 cajas de zapatos de mujer y 9 cajas de zapatos de hombre
E) 29 cajas de zapatos de mujer y 9 cajas de zapatos de hombre
Resolución
Rpta. : "E"
PREGUNTA 11
Sea u el número de decenas de sillas y v el número de decenas de mesas que fabrica una empresa al día. Si la utilidad diaria está dada por 200u+300v, y se tienen las siguientes restricciones:
u+v ≤4
2u+3v ≤10
40u+20v ≤120
encuentre el número de decenas de mesas y sillas, respectivamente, a fabricar diariamente de modo que la empresa obtenga la mayor utilidad.
A) 3 y 1
B) 1 y 3
C) 2 y 2
D) 2 y 3
E) 3 y 2
Resolución
En este tema se requiere determinar la región factible, la cual se obtiene mediante la representación geométrica de las restricciones dadas, para luego calcular las coordenadas de los vértices de la región y poder evaluar el máximo o mínimo valor de la función objetivo.
PLAN DE RESOLUCIÓN
I) Identificar la función objetivo.
II) Representación gráfica de las restricciones.
III) Evaluar la función objetivo en los vértices de la región factible.
Rpta. : "C"
PREGUNTA 12
Una fábrica produce dos tipos de cocinas: modelo A y modelo B. Producir una cocina del modelo A requiere dos horas de trabaja en máquina y dos horas de trabajo a mano. La venta de cada cocina del modelo A deja una utilidad de $ 40. De otro lado, producir una cocina del modelo B requiere cuatro horas de trabajo en máquina y una hora de trabajo a mano. La venta de cada unidad del modelo B deja una utilidad de$ 70. Si por día se dispone, en total, de un máximo de 200 horas de trabajo en máquina y de 140 horas de trabajo a mano, ¿cuál es la máxima utilidad diaria?
A) $ 3800
B) $ 3500
C) $ 3850
D) $ 2980
Resolución
Rpta. : "A"
PREGUNTA 13
Dadas las siguientes proposiciones respecto a la programación lineal:
I) Las restricciones de desigualdad son polinomios de primer y segundo grado
II) El punto óptimo se encuentra en la región admisible.
III) La región admisible contiene puntos, los cuales tienen alguna de sus coordenadas valor negativo
Son correctas:
A) Solo I
B) Solo III
C) Solo II
D) Solo I y II
E) Solo II y III
Resolución
I) Falso: pues las restricciones de desigualdad son funciones lineales.
II) Verdadero: pues la región admisible se ubica en el primer cuadrante (incluyendo los ejes coordenados); en esta región se encuentran las soluciones admisibles y obviamente se encuentra el punto óptimo.
III) Falso: pues ninguna solución admisible tiene coordenadas negativas.
Clave C
PREGUNTA 14
Con respecto a un problema de programación lineal, indique la secuencia correcta de verdad (V) o falsedad (F).
I) La función objetivo de un problema de programación lineal siempre posee máximo y mínimo. II) En un problema de programación lineal, pueden variarse los coeficientes de la función objetivo y aún mantenerse la solución óptima.
III) La región admisible de un problema de programación lineal es un polígono convexo.
A) VFF
B) FFV
C) VVV
D) FVF
E) VFV
Clave D
PREGUNTA 14
Resolución
Rpta. : "E"
PREGUNTA 15
Un club social encarga a una empresa de trasporte el viaje para llevar a los 1200 socios a ver la final de su equipo, la empresa dispone de autobús de 50 plazas y de microbuses de 30 plazas. El precio de cada viaje en el autobús es de 252 dólares y el del viaje en microbús de 180 dólares. Sabiendo que la empresa dispone de 28 conductores. ¿Cuál es el costo máximo del viaje?
A) 6125
B) 6000
C) 6002
D) 70000
E) 6336
Clave E
PREGUNTA 16
Erika tiene 80m2 de tela de algodón y 120m2 de tela de lana. Un traje requiere 1m2 de algodón y 3m2 de lana; y un vestido de mujer requiere 2m2 de cada una de las dos telas. Calcular el número de trajes y vestidos que debe confeccionar Erika para maximizar los beneficios; si un traje y un vestido se venden al mismo precio.
A) 20 trajes y 30 vestidos
B) 20 trajes y 18 vestidos
C) 35 trajes y 26 vestidos
D) 15 trajes y 30 vestidos
E) 27 trajes y 40 vestidos
Clave A
PREGUNTA 17
Una compañía aérea tiene dos aviones A y B para cubrir un determinado trayecto. El avión A debe hacer más o igual veces el trayecto que el avión B, pero no puede sobrepasar 120 viajes. Entre los aviones deben hacer más de 60 vuelos, pero no más de 200. En cada viaje del avión A, la empresa gana S/.300 000 y S/.200 000 por cada viaje de B. ¿Cuántos vuelos debe hacer cada avión para obtener la máxima ganancia?
A) 120;80
B) 140;60
C) 90;11
D) 50;150
E) 100;100
Clave A
PREGUNTA 18
Una empresa metal-mecánica utiliza una sección de planta para producir 2 tipos de bridas. La utilidad unitaria es de $5 para la brida con rosca y $4 para la brida sin rosca. La brida con rosca requiere 1 hora para su cepillado y 2 horas para su torneado. La brida sin rosca requiere 1 hora para su cepillado y 1 hora para su torneado. Se dispone de 220 horas para cepillar y 240 horas para tornear. Determine la máxima utilidad que se puede obtener y las cantidades de bridas fabricadas para ello.
A) $ 880; 0; 220
B) $ 600; 120; 0
C) $ 960; 40; 190
D) $1090; 210; 10
E) $ 900; 20; 200
Clave E
PREGUNTA 19
Una empresa de automóviles decide poner en el mercado dos tipos de autos económicos A y B, para ello solo dispone de S/.1800000, donde el costo de cada auto es de S/.30000 y S/.20000, respectivamente. Por exigencia del gerente, el número total de autos no debe ser superior a 80. Si el beneficio por la venta del tipo A es de S/.4000 y del tipo B es de S/.3000, ¿cuántos autos se deben fabricar de cada tipo para obtener el máximo beneficio?
A) 20;60
B) 20;50
C) 30;50
D) 50;40
E) 40;45
Clave A
PREGUNTA 20
Una compañía fabrica dos modelos de un producto, A y B. Se necesitan 20 minutos para fabricar el modelo A y 30 minutos para fabricar el modelo B; y un trabajo de 20 minutos de máquina para A y 10 minutos para B. Se dispone de 100 horas para su fabricación y 80 horas en máquina. Si se sabe que el beneficio por unidad es de S/150 y S/100 para A y B, respectivamente, halle la mejor producción para obtener el máximo beneficio.
A) 230 de A y 50 de B
B) 200 de A y 70 de B
C) 210 de A y 50 de B
D) 220 de A y 60 de B
E) 210 de A y 60 de B
Clave E
OBJETIVOS:
• Captar la idea de la programación lineal y sus posibilidades de aplicación a problemas prácticos.
• Dominar el lenguaje propio de la programación lineal: función objetivo, restricciones, región factible, etc...
• Aplicar las técnicas de resolución de sistemas de ecuaciones e inecuaciones lineales.
• Saber representar regiones factibles y determinar gráficamente los puntos donde puede darse la solución óptima.
• Saber encontrar esa solución óptima.
• Saber plantear un problema de programación lineal partiendo de su enunciado en términos generales.
Se llama programación lineal al conjunto de técnicas matemáticas que resuelven la situación de optimizar (maximizar o minimizar) una función objetivo sujeta a ciertas restricciones en la forma de desigualdades lineales.
En infinidad de aplicaciones de la industria, la economía, la estrategia militar, etc. se presentan situaciones en las que se exige maximizar o minimizar algunas funciones que se encuentran sujetas a determinadas limitaciones, que llamaremos restricciones.
PROGRAMACIÓN LINEAL
La programación lineal se puede definir como un medio matemático que busca la optimización (maximización o minimización) del uso de recursos limitados. La cual tiene por objeto ayudar a los responsables en la toma de decisiones sobre asuntos en donde intervienen un gran número de variables.
La representación matemática de dicho óptimo se conoce como función objetivo y consiste generalmente en maximizar utilidades, beneficios, ingresos, eficiencia o alguna medida efectiva; o en minimizar costos errogaciones, gastos ,etc. Toda limitación, condición o disponibilidad de los recursos o actividades se denomina restricción y debe expresarse matemáticamente por medio de desigualdad (no estricta) o igualdad. Tanto la función objetivo como las restricciones deben poderse escribir linealmente: de allí el nombre dado a este método: Programación Lineal (P.L.).
APLICACIONES DE LA REGIÓN FACTIBLE
Problemas de producción:
En estos problemas se trata de determinar la cantidad de productos que se deben fabricar para obtener los máximos beneficios en la venta de los mismos, o bien, calcular los mínimos costos en su fabricación.
Problemas de alimentación:
En estos problemas se trata de determinar la cantidad de cada uno de los alimentos que constituyen la alimentación diaria de un conjunto de personas o animales, de manera que el costo sea mínimo.
Problemas de transporte:
En estos problemas se trata de elegir el camino óptimo de envío de una mercancía desde varios orígenes (por ejemplo, plantas de producción) a diferentes destinos (centros de almacenamiento o consumo), de manera que el costo sea el mínimo.
DETERMINACIÓN DE LA REGIÓN FACTIBLE
La solución de la programación lineal, en el supuesto que exista, debe estar en la región determinada por las distintas desigualdades. Esta recibe el nombre de región factible, y puede estar o no acotada. La región factible incluye o no los lados y los vértices, según que las desigualdades sean en sentido amplio o en sentido estricto (< ó >). Si la región factible está acotada, su representación gráfica es un polígono convexo con un número de lados menor o igual que el número de restricciones.
El procedimiento para determinar la región factible es el siguiente:
i) Se resuelve cada inecuación por separado: Es decir, se encuentra el semiplano de soluciones de cada una de las inecuaciones.
• Se dibuja la recta asociada a la inecuación. Esta recta divide al plano en dos regiones o semiplanos.
• Para averiguar cuál es la región válida, el procedimiento práctico consiste en elegir un punto, por ejemplo, el (0;0) si la recta no pasa por el origen, y comprobar si las coordenadas satisfacen o no la inecuación. Si lo hacen, la región en la que está ese punto es aquella cuyos puntos verifican la inecuación; en caso contrario, la región válida es la otra.
ii) La región factible está formada por la intersección o región común de las soluciones de todas las inecuaciones. Como sucede con los sistemas de ecuaciones lineales, los sistemas de inecuaciones lineales pueden presentar varias opciones respecto a sus soluciones: puede no existir solución, en el caso de que exista el conjunto solución puede ser acotado o no.
MÉTODO ANALÍTICO O MÉTODO DE LOS VÉRTICES
Para aplicar este método es necesario seguir estos pasos:
• Hallar los puntos de corte de las rectas asociadas a las restricciones.
• Determinar los vértices de la región factible.
• Calcular los valores de la función objetivo para determinar la solución óptima.
La evaluación de la función objetivo en los vértices de la región factible permitirá encontrar la solución óptima.
El siguiente resultado, denominado teorema fundamental de la programación lineal, nos permite conocer otro método de solucionar un programa con dos variables.
En un programa lineal con dos variables, si existe una solución única que optimice la función objetivo, ésta se encuentra en un punto extremo (vértice) de la región factible acotada, nunca en el interior de dicha región.
Si la función objetivo toma el mismo valor óptimo en dos vértices, también toma idéntico valor en los puntos del segmento que determinan. En el caso de que la región factible no es acotada, la función lineal objetivo no alcanza necesariamente un valor óptimo concreto, pero, si lo hace, éste se encuentra en uno de los vértices de la región.
La evaluación de la función objetivo en los vértices de la región factible nos va a permitir encontrar el valor óptimo (máximo o mínimo) en alguno de ellos.
MÉTODO GRÁFICO O MÉTODO DE LAS RECTAS DE NIVEL
Las rectas de nivel dan los puntos del plano en los que la función objetivo toma el mismo valor. Para aplicar este método es necesario seguir estos pasos:
• Representar gráficamente la región factible.
• Representar las rectas de nivel.
• Determinar la solución óptima.
Para encontrar la solución óptima de una función objetivo a partir de las rectas de nivel, es necesario representarla y desplazarla paralelamente a sí misma dentro de la región factible hasta encontrar el vértice que determine dicha condición.
SOLUCIÓN GRÁFICA DE PROBLEMAS DE PROGRAMACIÓN LINEAL
Muchos problemas de administración y economía están relacionados con la optimización (maximización o minimización) de una función sujeta a un sistema de igualdades o desigualdades. La función por optimizar es la función objetivo. Las funciones de ganancia y de costo son ejemplos de funciones objetivo.
El sistema de igualdades o desigualdades a las que está sujeta la función objetivo reflejan las restricciones (por ejemplo, las limitaciones sobre recursos como materiales y mano de obra) impuestas a la solución (o soluciones) del problema.
Los problemas de esta naturaleza se llaman problemas de programación matemática. En particular, aquellas donde la función objetivo y las restricciones se expresan como ecuaciones o desigualdades lineales se llaman problemas de programación lineal.
Un problema de programación lineal consta de una función objetivo lineal por maximizar o minimizar, sujeta a ciertas restricciones en la forma de igualdades o desigualdades lineales. Desigualdades lineales se llaman problemas de programación lineal.
Siempre que el problema incluya únicamente dos o tres variables de decisión. podemos representar gráficamente las restricciones para dibujar en su intersección el poliedro convexo que conforma la región de factibilidad F.
Si el número de variables es dos, las restricciones, semiespacios cerrados, son semiplanos delimitados por la recta que corresponde a cada restricción.
Si el número de variables es tres, los semiespacios en este caso están delimitados por planos.
Para hallar gráficamente la solución de un problema de Programación Lineal con dos variables. procederemos del siguiente modo:
Paso 1: representaremos todas las restricciones del problema para determinar la región de factibilidad F. Si ésta es vacía, el problema no tiene solución óptima, se dice que es inconsistente. En otro caso. ir al paso 2.
Paso 2: identificar los extremos o vértices de F.
Paso 3: dibujar una de las rectas que pertenece a la familia de rectas paralelas que representa la función objetivo f(x;y)=k. Habitualmente. suele dibujarse f(x;y)=0 por comodidad.
Paso 4: desplazamos en forma paralela a sí misma la recta que representa la función objetivo para determinar la dirección de mejora que será aumento o disminución según si el objetivo del problema es la maximización o minimización de dicha función.
Paso 5: el punto extremo de F al que corresponde el valor óptimo para la recta que representa la función objetivo es la solución óptima finita del problema.
Hay que tener en cuenta que pueden presentarse las situaciones estudiadas en el apartado anterior, cuando existe más de un punto extremo o la región de factibilidad es no acotada. Como ejemplo de un problema de programación lineal en que la función objetivo debe maximizarse
RESUMEN
La programación lineal es una técnica que facilita la resolución de problemas de planificación económica o social. Su objetivo es optimizar, es decir, reducir los costos elevados o elevar los beneficios, utilizando las restricciones o condiciones impuestas por el problema. Así también en lugar de maximizar se puede minimizar y cambiar el sentido de las desigualdades. Intervienen:
• La función Z = ax+by+c se llama función objetivo y es la que se va a optimizar.
• En la expresión, x e y son las variables de decisión, mientras que a, b y c son constantes.
• Las restricciones son las inecuaciones lineales. Su número lo define el problema.
• Al conjunto de valores de x e y que verifican cada una de las restricciones en su totalidad se le denomina conjunto (o región) factible. Todo punto de ese conjunto puede ser solución del problema.
• La solución óptima del problema será un par de valores (x0; y0) del conjunto factible que haga que Z tome el valor máximo o mínimo. La cantidad que se desea maximizar o minimizar se expresa en forma de ecuaciones lineales.
Las restricciones que imponen las condiciones de los problemas se expresan en forma de inecuaciones lineales.
Para la resolución de un problema de programación lineal se tiene tres tipos de métodos:
• Método práctico.
• Método analítico o de los vértices.
• Método gráfico o de las rectas de nivel.
MÉTODO PRÁCTICO
Para resolver un problema de programación lineal, es necesario seguir estos pasos:
• Planteamiento.
• Determinación de la región factible.
• Determinación de la solución óptima.
PLANTEAMIENTO:
Para plantear un problema de programación lineal se debe:
• Organizar la información mediante una tabla.
• Asignar una variable a cada una de la incógnitas.
• Determinar las restricciones que se crean conveniente.
• Determinar la función objetivo.
DETERMINACIÓN DE LA REGIÓN FACTIBLE:
La solución de la programación lineal, en el supuesto que exista, debe estar en la región determinada por las distintas desigualdades. Esta recibe el nombre de región factible, y puede estar o no acotada. El procedimiento para determinar la región factible es el siguiente:
• Se resuelve cada inecuación por separado, es decir, se encuentra el semiplano de soluciones de cada una de las inecuaciones.
• La región factible está formada por la intersección o región común de las soluciones de todas las inecuaciones.
Determinación de la solución óptima: La solución óptima es aquella que maximiza o minimiza la función objetivo. Dicha solución se encuentra en la frontera de la región factible.
TIPOS DE SOLUCIONES
Los tipos de soluciones que se presentan en los problemas de programación lineal con dos incógnitas pueden ser:
FACTIBLES: Aquellas que tienen un conjunto de soluciones o valores que satisfacen las restricciones del problema.
NO FACTIBLES: Aquellas que no tienen un conjunto de soluciones que cumplan con las restricciones del problema.
SOLUCIÓN FACTIBLE:
SOLUCIÓN ÚNICA: Una solución es única cuando la solución óptima se encuentra sólo en uno de los vértices de la región factible.
SOLUCIÓN MÚLTIPLE: Una solución es múltiple cuando hay infinitas soluciones que corresponden a los puntos del segmento que tiene por extremos a dos vértices de la región factible.
SOLUCIÓN NO ACOTADA: Una solución no es acotada cuando la función objetivo no tiene valores extremos, pues la región factible es no acotada.
SOLUCIÓN NO FACTIBLE: Una solución es no factible cuando no existe la región factible por falta de puntos comunes en el sistema de inecuaciones.